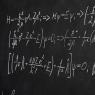Modul vzorce vektorového součinu vektorů. Křížový součin vektorů, definice, vlastnosti

Je zřejmé, že v případě vektorového produktu záleží na pořadí, ve kterém jsou vektory přijímány, navíc,

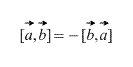
Také přímo z definice vyplývá, že pro jakýkoli skalární faktor k (číslo) platí následující:

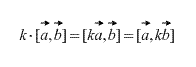
Křížový součin kolineárních vektorů se rovná nulovému vektoru. Kromě toho je křížový součin dvou vektorů nulový právě tehdy, když jsou kolineární. (V případě, že jeden z nich je nulový vektor, je nutné pamatovat na to, že nulový vektor je podle definice kolineární s libovolným vektorem).

Vektorový součin má distribuční vlastnictví, to je

Vyjádření vektorového součinu pomocí souřadnic vektorů.

Nechť jsou dány dva vektory

(jak zjistit souřadnice vektoru ze souřadnic jeho začátku a konce - viz článek Bodový součin vektorů, položka Alternativní definice bodového součinu aneb výpočet bodového součinu dvou vektorů určených jejich souřadnicemi.)

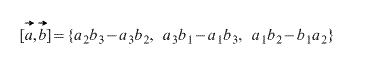
Proč potřebujete vektorový produkt?

Existuje mnoho způsobů, jak použít křížový součin, například jak je napsáno výše, výpočtem křížového součinu dvou vektorů můžete zjistit, zda jsou kolineární.

Nebo jej lze použít jako způsob výpočtu plochy rovnoběžníku zkonstruovaného z těchto vektorů. Na základě definice je délka výsledného vektoru plocha daného rovnoběžníku.

Obrovské množství aplikací je také v elektřině a magnetismu.

Online kalkulačka vektorových produktů.

Chcete-li pomocí této kalkulačky najít skalární součin dvou vektorů, musíte zadat souřadnice prvního vektoru do prvního řádku v pořadí a druhého do druhého řádku. Souřadnice vektorů lze vypočítat ze souřadnic jejich začátku a konce (viz článek Bodový součin vektorů, položka Alternativní definice bodového součinu neboli výpočet bodového součinu dvou vektorů daného jejich souřadnicemi.)

7.1. Definice křížového produktu

Tři nekoplanární vektory a, b a c, brané v uvedeném pořadí, tvoří pravotočivý triplet, jestliže od konce třetího vektoru c nejkratší odbočka z prvního vektoru a do druhého vektoru b být proti směru hodinových ručiček a levotočivý triplet ve směru hodinových ručiček (viz obr. .16).

Vektorový součin vektoru a a vektoru b se nazývá vektor c, který:

1. Kolmo k vektorům a a b, tj. c ^ a a c ^ b;

2. Má délku číselně rovnou ploše rovnoběžníku konstruovaného na vektorech aab jako na bocích (viz obr. 17), tzn.

3. Vektory a, b a c tvoří pravotočivou trojici.

Křížový součin se označuje a x b nebo [a,b]. Následující vztahy mezi jednotkovými vektory přímo vyplývají z definice vektorového součinu, j A k

(viz obr. 18):
i x j = k, j x k = i, k x i = j. Dokažme to například

i xj = k. ^ 1) k ^ i, k

j; 2) |k |=1, ale | i x j

| = |i | A|J | sin(90°)=1;

3) vektory i, ja

tvoří pravou trojici (viz obr. 16).

7.2. Vlastnosti křížového produktu = -(1. Při přeskupování faktorů vektorový součin mění znaménko, tzn.).

a xb = (b xa) (viz obr. 19).

Vektory a xb a b xa jsou kolineární, mají stejné moduly (plocha rovnoběžníku zůstává nezměněna), ale jsou opačně orientované (trojice a, b, a xb a a, b, b x a opačné orientace). Proto axb b xa b 2. Vektorový součin má kombinační vlastnost vzhledem ke skalárnímu faktoru, tj. l (a xb) = (la) x b = a x (l b). b Nechť l >0. Vektor l (a xb) je kolmý na vektory a a b. vektor ( axb l axb sekera axb b xa b je také kolmá k vektorům a a

(vektory a, axb ale leží ve stejné rovině). To znamená, že vektory axb(a xb) a ( axb<0.

kolineární. Je zřejmé, že jejich směry se shodují. Mají stejnou délku: b Proto<=>(a xb)=

a xb. Obdobným způsobem se dokazuje pro

3. Dva nenulové vektory aa

(jsou kolineární právě tehdy, když je jejich vektorový součin roven nulovému vektoru, tj. a ||b a xb = 0. b Konkrétně i *i =j *j =k *k =0.

4. Vektorový součin má distribuční vlastnost:

a+b)

xc = a xc + Následující vztahy mezi jednotkovými vektory přímo vyplývají z definice vektorového součinu, xs.

Přijmeme bez dokladu.

7.3. Vyjádření křížového součinu pomocí souřadnic Následující vztahy mezi jednotkovými vektory přímo vyplývají z definice vektorového součinu, Použijeme křížovou součinovou tabulku vektorů i, A a k: pokud se směr nejkratší cesty z prvního vektoru do druhého shoduje se směrem šipky, pak se součin rovná třetímu vektoru, pokud se neshoduje, bere se třetí vektor se znaménkem mínus. Nechť jsou dány dva vektory a =a x i +a y Následující vztahy mezi jednotkovými vektory přímo vyplývají z definice vektorového součinu,+a z A a b = b x

protože pravá strana rovnosti (7.1) odpovídá rozšíření determinantu třetího řádu z hlediska prvků prvního řádku Rovnost (7.2) je snadno zapamatovatelná.

7.4. Některé aplikace křížového produktu

Stanovení kolinearity vektorů

Nalezení oblasti rovnoběžníku a trojúhelníku

Podle definice vektorového součinu vektorů A a b |a xb | =|a | * |b |sin g, tj. S párů = |a x b |. A proto D S = 1/2|a x b |.

Určení momentu síly k bodu

Nechť v bodě A působí síla F = AB a nechat O- nějaký bod v prostoru (viz obr. 20).

Z fyziky je známo, že moment síly F vzhledem k bodu O nazývaný vektor M, která prochází bodem O A:

1) kolmo k rovině procházející body O, A, B;

2) číselně se rovná součinu síly na rameno

3) tvoří pravou trojici s vektory OA a A B.

Proto M = OA x F.

Nalezení lineární rychlosti otáčení

Rychlost proti bod M tuhého tělesa rotujícího úhlovou rychlostí w kolem pevné osy, je určeno Eulerovým vzorcem v =w xr, kde r =OM, kde O je nějaký pevný bod osy (viz obr. 21).

SMÍŠENÝ PRODUKT TŘÍ VEKTORŮ A JEHO VLASTNOSTI

Smíšená práce tři vektory se nazývá číslo rovné . Určeno . Zde jsou první dva vektory násobeny vektorově a následně je výsledný vektor násoben skalárně třetím vektorem. Je zřejmé, že takový produkt je určitý počet.

Uvažujme vlastnosti smíšeného produktu.

Geometrický význam smíšená práce. Smíšený součin 3 vektorů až do znaménka se rovná objemu kvádru postaveného na těchto vektorech, jako na hranách, tzn. .
Tak a .

Důkaz. Nechme stranou vektory ze společného počátku a sestrojme na nich rovnoběžnostěn. Označme a poznamenejme, že . Podle definice skalárního součinu

Za předpokladu, že a označující tím h zjistěte výšku rovnoběžnostěnu.

Tedy, když

Pokud, tak ano. Proto, .

Kombinací obou těchto případů dostaneme nebo .

Z důkazu této vlastnosti zejména vyplývá, že je-li trojice vektorů pravotočivá, pak smíšený součin je , a je-li levotočivý, pak .
Pro všechny vektory , platí rovnost
Důkaz této vlastnosti vyplývá z vlastnosti 1. Je skutečně snadné prokázat, že a . Kromě toho se znaménka „+“ a „–“ berou současně, protože úhly mezi vektory a a a jsou ostré i tupé.
Když jsou jakékoli dva faktory přeskupeny, smíšený produkt změní znaménko.
Pokud totiž uvažujeme smíšený produkt, pak např. popř
Smíšený součin tehdy a jen tehdy, když je jeden z faktorů roven nule nebo jsou vektory koplanární.
Důkaz.

Nezbytnou a postačující podmínkou pro koplanaritu 3 vektorů je tedy to, že jejich smíšený součin je roven nule. Navíc z toho plyne, že tři vektory tvoří základ v prostoru if .

Pokud jsou vektory uvedeny v souřadnicovém tvaru, pak lze ukázat, že jejich smíšený součin lze nalézt podle vzorce:

.

Smíšený součin se tedy rovná determinantu třetího řádu, který má souřadnice prvního vektoru v prvním řádku, souřadnice druhého vektoru ve druhém řádku a souřadnice třetího vektoru ve třetím řádku.

Příklady.

ANALYTICKÁ GEOMETRIE V PROSTORU

Rovnice F(x, y, z)= 0 definuje v prostoru Oxyz nějaký povrch, tzn. místo bodů, jejichž souřadnice x, y, z splnit tuto rovnici. Tato rovnice se nazývá povrchová rovnice a x, y, z– aktuální souřadnice.

Často však povrch není specifikován rovnicí, ale jako množina bodů v prostoru, které mají tu či onu vlastnost. V tomto případě je nutné najít rovnici povrchu na základě jeho geometrických vlastností.

ROVINA.

NORMÁLNÍ ROVINNÝ VEKTOR.

ROVNICE LETADLA PROLETUJÍCÍHO DANÝM BODEM

Uvažujme libovolnou rovinu σ v prostoru. Jeho poloha je určena určením vektoru kolmého k této rovině a nějakého pevného bodu M0(x 0, y 0, z 0), ležící v rovině σ.

Vektor kolmý k rovině σ se nazývá normální vektor této roviny. Nechť má vektor souřadnice .

Odvoďme rovnici roviny σ procházející tímto bodem M0 a mající normální vektor. K tomu vezměte libovolný bod v rovině σ M(x, y, z) a zvažte vektor .

Za jakýkoli bod MО σ je vektor Proto je jejich skalární součin roven nule. Tato rovnost je podmínkou, že bod MО σ. Platí pro všechny body této roviny a je porušeno, jakmile bod M bude mimo rovinu σ.

Označíme-li body poloměrovým vektorem M, – vektor poloměru bodu M0, pak lze rovnici zapsat ve tvaru

Tato rovnice se nazývá vektor rovinná rovnice. Pojďme to napsat v souřadnicovém tvaru. Od té doby

Získali jsme tedy rovnici roviny procházející tímto bodem. K vytvoření rovnice roviny tedy potřebujete znát souřadnice normálového vektoru a souřadnice nějakého bodu ležícího v rovině.

Všimněte si, že rovnice roviny je rovnicí 1. stupně vzhledem k aktuálním souřadnicím x, y A z.

Příklady.

OBECNÁ ROVNICE LETADLA

Lze ukázat, že jakákoli rovnice prvního stupně s ohledem na kartézské souřadnice x, y, z představuje rovnici nějaké roviny. Tato rovnice je napsána takto:

Ax+By+Cz+D=0

a nazývá se obecná rovnice rovinu a souřadnice A, B, C zde jsou souřadnice normálového vektoru roviny.

Uvažujme speciální případy obecné rovnice. Pojďme zjistit, jak je rovina umístěna vzhledem k souřadnicovému systému, pokud se jeden nebo více koeficientů rovnice stane nulou.

A je délka segmentu odříznutého rovinou na ose Vůl. Podobně lze ukázat, že b A C– délky segmentů odříznutých uvažovanou rovinou na osách Oj A Oz.

Pro konstrukci rovin je vhodné použít rovnici roviny v úsecích.

Než uvedeme pojem vektorového součinu, přejděme k otázce orientace uspořádané trojice vektorů a →, b →, c → v trojrozměrném prostoru.

Pro začátek odložme vektory a → , b → , c → z jednoho bodu. Orientace trojice a → , b → , c → může být pravá nebo levá v závislosti na směru samotného vektoru c →. Typ trojice a → , b → , c → určíme ze směru, ve kterém je nejkratší obrat z vektoru a → do b → od konce vektoru c → .

Pokud nejkratší zatáčku provedeme proti směru hodinových ručiček, nazývá se trojice vektorů a → , b → , c → právo, pokud ve směru hodinových ručiček - vlevo.

Dále vezměte dva nekolineární vektory a → a b →. Nakreslete potom vektory A B → = a → a A C → = b → z bodu A. Sestrojme vektor A D → = c →, který je současně kolmý k A B → i A C →. Při konstrukci samotného vektoru A D → = c → to tedy můžeme udělat dvěma způsoby, dáme mu buď jeden směr, nebo opačný (viz obrázek).

Uspořádaná trojice vektorů a → , b → , c → může být, jak jsme zjistili, pravá nebo levá v závislosti na směru vektoru.

Z výše uvedeného můžeme zavést definici vektorového součinu. Tato definice je dána pro dva vektory definované v pravoúhlém souřadnicovém systému trojrozměrného prostoru.

Definice 1

Vektorový součin dvou vektorů a → a b → budeme nazývat takový vektor definovaný v pravoúhlém souřadnicovém systému trojrozměrného prostoru tak, že:

pokud jsou vektory a → a b → kolineární, bude nula;
bude kolmá jak k vektoru a → , tak k vektoru b → tzn. ∠ a → c → = ∠ b → c → = π 2 ;
jeho délka je určena vzorcem: c → = a → · b → · sin ∠ a → , b → ;
trojice vektorů a → , b → , c → má stejnou orientaci jako daný souřadnicový systém.

Vektorový součin vektorů a → a b → má následující zápis: a → × b →.

Souřadnice vektorového součinu

Protože jakýkoli vektor má v souřadnicovém systému určité souřadnice, můžeme zavést druhou definici vektorového součinu, která nám umožní najít jeho souřadnice pomocí zadaných souřadnic vektorů.

Definice 2

V pravoúhlém souřadnicovém systému trojrozměrného prostoru vektorový součin dvou vektorů a → = (a x ; a y ; a z) a b → = (b x ; b y ; b z) se nazývá vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kde i → , j → , k → jsou souřadnicové vektory.

Vektorový součin lze znázornit jako determinant čtvercové matice třetího řádu, kde první řádek obsahuje vektorové vektory i → , j → , k → , druhý řádek obsahuje souřadnice vektoru a → a třetí řádek obsahuje souřadnice vektoru b → v daném pravoúhlém souřadnicovém systému, toto je determinant matice vypadá takto: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Rozšířením tohoto determinantu na prvky prvního řádku získáme rovnost: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Vlastnosti křížového produktu

Je známo, že vektorový součin v souřadnicích je reprezentován jako determinant matice c → = a → × b → = i → j → k → a x a y a z b x b y b z , pak na zákl. vlastnosti maticového determinantu zobrazí se následující vlastnosti vektorového produktu:

antikomutativnost a → × b → = - b → × a → ;
distributivita a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → nebo a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
asociativita λ a → × b → = λ a → × b → nebo a → × (λ b →) = λ a → × b →, kde λ je libovolné reálné číslo.

Tyto vlastnosti mají jednoduché důkazy.

Jako příklad můžeme dokázat antikomutativní vlastnost vektorového součinu.

Důkaz antikomutativnosti

Podle definice a → × b → = i → j → k → a x a y a z b x b y b z a b → × a → = i → j → k → b x b y b z a x a y az . A pokud jsou dva řádky matice prohozeny, pak by se hodnota determinantu matice měla změnit na opačnou, tedy a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , což a dokazuje, že vektorový součin je antikomutativní.

Vektorový součin - příklady a řešení

Ve většině případů se jedná o tři typy problémů.

V úlohách prvního typu se obvykle uvádějí délky dvou vektorů a úhel mezi nimi a je potřeba zjistit délku vektorového součinu. V tomto případě použijte následující vzorec c → = a → · b → · sin ∠ a → , b → .

Příklad 1

Najděte délku vektorového součinu vektorů a → a b →, pokud znáte a → = 3, b → = 5, ∠ a →, b → = π 4.

Řešení

Určením délky vektorového součinu vektorů a → a b → vyřešíme tento problém: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Odpověď: 15 2 2 .

Úlohy druhého typu mají souvislost se souřadnicemi vektorů, v nich vektorový součin, jeho délka atd. se hledají přes známé souřadnice daných vektorů a → = (a x; a y; a z) A b → = (b x ; b y ; b z) .

U tohoto typu problému můžete vyřešit spoustu možností úloh. Například nelze zadat souřadnice vektorů a → a b →, ale jejich expanze do souřadnicových vektorů tvaru b → = b x · i → + b y · j → + b z · k → a c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, nebo vektory a → a b → lze specifikovat souřadnicemi jejich počátku a koncové body.

Zvažte následující příklady.

Příklad 2

V pravoúhlém souřadnicovém systému jsou dány dva vektory: a → = (2; 1; - 3), b → = (0; - 1; 1). Najděte jejich křížový produkt.

Řešení

Podle druhé definice najdeme vektorový součin dvou vektorů v daných souřadnicích: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Pokud vektorový součin zapíšeme přes determinant matice, pak řešení tohoto příkladu vypadá takto: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Odpověď: a → × b → = - 2 i → - 2 j → - 2 k → .

Příklad 3

Najděte délku vektorového součinu vektorů i → - j → a i → + j → + k →, kde i →, j →, k → jsou jednotkové vektory pravoúhlého kartézského souřadnicového systému.

Řešení

Nejprve najdeme souřadnice daného vektorového součinu i → - j → × i → + j → + k → v daném pravoúhlém souřadném systému.

Je známo, že vektory i → - j → a i → + j → + k → mají souřadnice (1; - 1; 0) a (1; 1; 1). Zjistíme délku vektorového součinu pomocí determinantu matice, pak máme i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Proto vektorový součin i → - j → × i → + j → + k → má souřadnice (- 1 ; - 1 ; 2) v daném souřadnicovém systému.

Délku vektorového součinu zjistíme pomocí vzorce (viz část o zjištění délky vektoru): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Odpověď: i → - j → × i → + j → + k → = 6 . .

Příklad 4

V pravoúhlém kartézském souřadnicovém systému jsou uvedeny souřadnice tří bodů A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Najděte nějaký vektor kolmý k A B → a A C → současně.

Řešení

Vektory A B → a AC → mají následující souřadnice (-1; 2; 2) a (0; 4; 1). Po nalezení vektorového součinu vektorů A B → a A C → je zřejmé, že jde o vektor kolmý podle definice k A B → i A C →, to znamená, že je řešením našeho problému. Najdeme to A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Odpověď: - 6 i → + j → - 4 k → . - jeden z kolmých vektorů.

Problémy třetího typu jsou zaměřeny na využití vlastností vektorového součinu vektorů. Po jeho aplikaci získáme řešení daného problému.

Příklad 5

Vektory a → a b → jsou kolmé a jejich délky jsou 3 a 4. Najděte délku vektorového součinu 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Řešení

Distributivní vlastností vektorového součinu můžeme napsat 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Vlastností asociativnosti odebereme číselné koeficienty ze znaménka vektorových součinů v posledním výrazu: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektorové součiny a → × a → a b → × b → se rovnají 0, protože a → × a → = a → · a → · sin 0 = 0 a b → × b → = b → · b → · sin 0 = 0, pak 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Z antikomutativnosti vektorového součinu vyplývá - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Pomocí vlastností vektorového součinu získáme rovnost 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Podle podmínky jsou vektory a → a b → kolmé, to znamená, že úhel mezi nimi je roven π 2. Nyní zbývá pouze dosadit nalezené hodnoty do příslušných vzorců: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Odpověď: 3 a → - b → × a → - 2 b → = 60.

Délka vektorového součinu vektorů je podle definice rovna a → × b → = a → · b → · sin ∠ a → , b → . Protože je již známo (ze školního kurzu), že plocha trojúhelníku se rovná polovině součinu délek jeho dvou stran vynásobených sinem úhlu mezi těmito stranami. V důsledku toho se délka vektorového součinu rovná ploše rovnoběžníku - zdvojeného trojúhelníku, konkrétně součinu stran ve formě vektorů a → a b →, položených z jednoho bodu sinem úhel mezi nimi sin ∠ a →, b →.

Toto je geometrický význam vektorového součinu.

Fyzikální význam vektorového součinu

V mechanice, jednom z odvětví fyziky, můžete díky vektorovému součinu určit moment síly vzhledem k bodu v prostoru.

Definice 3

Momentem síly F → působící na bod B vzhledem k bodu A budeme chápat následující vektorový součin A B → × F →.

Pokud si všimnete chyby v textu, zvýrazněte ji a stiskněte Ctrl+Enter

Definice. Vektorový součin vektoru a a vektoru b je vektor označený symbolem [α, b] (nebo l x b), takže 1) délka vektoru [a, b] je rovna (p, kde y je úhel mezi vektory a a b ( obr. 31) vektor [a, b) je kolmý na vektory a a b, tzn. kolmé k rovině těchto vektorů; 3) vektor [a, b] je nasměrován tak, že od konce tohoto vektoru je vidět nejkratší obrat z a do b proti směru hodinových ručiček (obr. 32). Rýže. 32 Obr.31 Jinými slovy, vektory a, b a [a, b) tvoří pravostranný triplet vektorů, tzn. umístěné jako palec, ukazováček a prostředníček pravé ruky. Pokud jsou vektory a a b kolineární, budeme předpokládat, že [a, b] = 0. Podle definice je délka vektorového součinu číselně rovna ploše Sa rovnoběžníku (obr. 33), sestrojeného na vynásobeném vektory a a b jako strany: 6.1 . Vlastnosti vektorového součinu 1. Vektorový součin je roven nulovému vektoru právě tehdy, když je alespoň jeden z vynásobených vektorů nulový nebo když jsou tyto vektory kolineární (jsou-li vektory a a b kolineární, pak úhel mezi nimi je buď 0 nebo 7r). Najděte oblast trojúhelníku (obr. 36). Je zřejmé, že plocha b"d trojúhelníku OAO je rovna polovině plochy S rovnoběžníku O AC B. Výpočtem vektorového součinu (a, b| vektorů a = OA a b = ob získáme Poznámka: Vektorový součin není asociativní, tj. rovnost ( (a, b),c) = [a, |b,c)) v obecném případě neplatí. Například pro a = ss j máme §. 7. Smíšený součin vektorů Vynásobme vektory a, b, c a 1> vektorem [a, 1>] ), c).Číslo ([a, b], e) se nazývá smíšený součin vektorů a, b a značí se symbolem (a, 1), vektory a, b a c jsou nazývaný v tomto případě koplanární), pak smíšený součin ([a, b], c) = 0. To vyplývá ze skutečnosti, že vektor [a, b| je kolmý k rovině, ve které leží vektory a a 1. ", a tedy k vektoru c. / Pokud body O, A, B, C neleží ve stejné rovině (vektory a, b a c jsou nekoplanární), sestrojíme na hranách OA rovnoběžnostěn, OB a OS (obr. 38 a). Podle definice vektorového součinu máme (a,b) = So c, kde So je plocha rovnoběžníku OADB a c je jednotkový vektor kolmý na vektory a a b a takový, že trojice a , b, c je pravotočivá, tzn. vektory a, b a c jsou umístěny jako palec, ukazováček a prostředníček pravé ruky (obr. 38 b). Vynásobením obou stran poslední rovnosti zprava skalárně vektorem c získáme vektorový součin vektorů daný souřadnicemi. Smíšená práce. Číslo pc c se rovná výšce h sestrojeného rovnoběžnostěnu se znaménkem „+“, pokud je úhel mezi vektory c a c ostrý (trojité a, b, c – vpravo), a se znaménkem „-“ znaménko, pokud je úhel tupý (trojitý a, b, c - vlevo), takže smíšený součin vektorů a, b a c je roven objemu V kvádru postaveného na těchto vektorech jako na hranách, pokud trojité a, b, c je vpravo a -V, pokud trojité a , b, c - vlevo. Na základě geometrického významu smíšeného součinu můžeme usoudit, že vynásobením stejných vektorů a, b a c v libovolném jiném pořadí vždy dostaneme buď +7 nebo -K. Značka výrobce Obr. 38 reference bude záviset pouze na tom, jakou trojici tvoří vynásobené vektory - vpravo nebo vlevo. Pokud vektory a, b, c tvoří pravotočivou trojici, pak trojice b, c, a a c, a, b budou také pravotočivé. Přitom všechny tři trojice b, a, c; a, c, b a c, b, a - vlevo. Tedy (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b , A). Znovu zdůrazňujeme, že smíšený součin vektorů je roven nule pouze tehdy, jsou-li vynásobené vektory a, b, c koplanární: (a, b, c jsou koplanární) 7.2. Smíšený součin v souřadnicích Nechť jsou vektory a, b, c dány jejich souřadnicemi v bázi i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Najdeme výraz pro jejich smíšený součin (a, b, c). Máme smíšený součin vektorů specifikovaných jejich souřadnicemi v bázi i, J, k, rovný determinantu třetího řádu, jehož čáry jsou složeny příslušně ze souřadnic prvního, druhého a třetího vynásobeného vektoru. Nezbytnou a postačující podmínku pro koplanaritu vektorů a y\, Z|), b = (хъ У2.22), с = (жз, з, 23) zapíšeme ve tvaru У| z, ag2 y2-2 =0. Příklad Uz. Zkontrolujte, zda jsou vektory „ = (7,4,6), b = (2, 1,1), c = (19, II, 17) koplanární. Vypočítejte výšku h rovnoběžnostěnu postaveného na vektorech a = 31 + 2j - 5k, b = i- j + 4knc = i-3j + k, jestliže za základ vezmeme rovnoběžník postavený na vektorech a a I. Odpovědi