Jaké úhly v lichoběžníku jsou stejné? Lichoběžník

FGKOU "MKK" Penzion pro žáky Ministerstva obrany Ruské federace"

"SCHVÁLENÝ"

Vedoucí samostatné disciplíny

(matematika, informatika a ICT)

Yu. V. Krylová _____________

"___" ______________ 2015

« Trapéz a jeho vlastnosti»

Metodický vývoj

učitel matematiky

Shatalina Elena Dmitrievna

Zkontrolováno a

na zasedání PMO ze dne _______________

Protokol č.______

Moskva

2015

Obsah

Úvod 2

Definice 3

Vlastnosti rovnoramenného lichoběžníku 4

Vepsané a opsané kružnice 7

Vlastnosti vepsaných a opsaných lichoběžníků 8

Průměrné hodnoty v lichoběžníku 12

Vlastnosti libovolného lichoběžníku 15

Známky lichoběžníku 18

Dodatečné konstrukce v lichoběžníku 20

Lichoběžníková plocha 25

10. Závěr

Seznam použité literatury

Aplikace

Doklady některých vlastností lichoběžníku 27

Úkoly pro samostatnou práci

Problémy na téma „lichoběžník“ se zvýšenou složitostí

Screeningový test na téma „lichoběžník“

Zavedení

Tato práce je věnována geometrickému útvaru zvanému lichoběžník. "Obyčejná postava," řeknete, ale není tomu tak. Je opředena mnoha tajemstvími a záhadami, když se na ni podíváte blíže a budete ji dále studovat, objevíte ve světě geometrie spoustu nových věcí, které se vám dosud neřešily.

Lichoběžník - řecké slovo trapezion - "stůl". Půjčování v 18. století z lat. jazyk, kde trapéz je řečtina. Je to čtyřúhelník, jehož dvě protilehlé strany jsou rovnoběžné. S lichoběžníkem se poprvé setkal starověký řecký vědec Posidonius (2. století před naším letopočtem). V našem životě je mnoho různých postav. V 7. třídě jsme se blíže seznámili s trojúhelníkem v 8. třídě jsme se podle školního vzdělávacího programu začali zabývat lichoběžníkem; Tento údaj nás zaujal a v učebnici se o něm píše nepřípustně málo. Proto jsme se rozhodli vzít tuto záležitost do svých rukou a najít informace o lichoběžníku. jeho vlastnosti.

Práce zkoumá vlastnosti známé studentům z látky probírané v učebnici, ale většinou neznámé vlastnosti, které jsou nezbytné pro řešení složitých problémů. Čím větší počet řešených problémů, tím více otázek při jejich řešení vzniká. Odpověď na tyto otázky se někdy jeví jako záhada, poznáváním nových vlastností lichoběžníku, neobvyklých metod řešení problémů i techniky doplňkových konstrukcí postupně objevujeme tajemství lichoběžníku. Na internetu, když to zadáte do vyhledávače, je velmi málo literatury o metodách řešení problémů na téma „lichoběžník“. V průběhu práce na projektu bylo nalezeno velké množství informací, které studentům pomohou při hloubkovém studiu geometrie.

Lichoběžník.

Definice

Lichoběžník – čtyřúhelník, ve kterém je pouze jedna dvojice stran rovnoběžná (a druhá dvojice stran rovnoběžná).

Rovnoběžné strany lichoběžníku se nazývají důvodů. .
Další dvě jsou strany Pokud jsou strany stejné, nazývá se lichoběžník

rovnoramenný Lichoběžník, který má na svých stranách pravé úhly, se nazývá

obdélníkovýSegment spojující středy stran se nazývá.

střední čára lichoběžníku

2 Vzdálenost mezi základnami se nazývá výška lichoběžníku.

3. Vlastnosti rovnoramenného lichoběžníku

1
. Úhlopříčky rovnoramenného lichoběžníku jsou stejné.

0. Průmět boční strany rovnoramenného lichoběžníku na větší základnu je roven polovině rozdílu základen a průmět úhlopříčky je roven součtu základen.

3. Kruh vepsaný a opsaný

Pokud se součet základen lichoběžníku rovná součtu stran, lze do něj vepsat kružnici.
E

Pokud je lichoběžník rovnoramenný, lze kolem něj popsat kruh.

4. Vlastnosti vepsaných a opsaných lichoběžníků

2.Pokud lze kružnici vepsat do rovnoramenného lichoběžníku, pak

4 . součet délek základen se rovná součtu délek stran. Proto je délka laterální strany rovna délce střední čáry lichoběžníku.

Je-li kružnice vepsána do lichoběžníku, jsou strany od jejího středu viditelné pod úhlem 90°. Pokud je kruh vepsán do lichoběžníku a dotýká se jedné ze stran, rozděluje jej na segmenty m , a n

1

0 pak se poloměr vepsané kružnice rovná geometrickému průměru těchto segmentů.

. Pokud je kruh postaven na menší základně lichoběžníku jako průměr, prochází středy úhlopříček a dotýká se spodní základny, pak jsou úhly lichoběžníku 30°, 30°, 150°, 150°.

5. Průměrné hodnoty v lichoběžníku

Geometrický průměr V libovolném lichoběžníku se základnami A A b Pro > Ab :

nerovnost je pravdivá

6. Vlastnosti libovolného lichoběžníku

1
. Středy úhlopříček lichoběžníku a středy bočních stran leží na stejné přímce.

2. Osy úhlů přiléhajících k jedné z bočních stran lichoběžníku jsou kolmé a protínají se v bodě ležícím na střední čáře lichoběžníku, tj. když se protnou, vznikne pravoúhlý trojúhelník s přeponou rovnou boční strana.

3. Úseky přímky rovnoběžné se základnami lichoběžníku, protínající boční strany a úhlopříčky lichoběžníku, uzavřené mezi boční stranou a úhlopříčkou, jsou stejné.

Průsečík pokračování stran libovolného lichoběžníku, průsečík jeho úhlopříček a středy základen leží na téže přímce.

5. Když se protnou úhlopříčky libovolného lichoběžníku, vzniknou čtyři trojúhelníky se společným vrcholem a trojúhelníky sousedící se základnami jsou podobné a trojúhelníky sousedící se stranami mají stejnou velikost (tj. mají stejnou plochu).

6. Součet druhých mocnin úhlopříček libovolného lichoběžníku se rovná součtu čtverců bočních stran přičtených k dvojnásobku součinu základen.

d 1 2 + d 2 2 = C 2 + d 2 + 2 ab

7
. V pravoúhlém lichoběžníku se rozdíl čtverců úhlopříček rovná rozdílu čtverců základen d 1 2 - d 2 2 = V libovolném lichoběžníku se základnami 2 – A 2

8 . Přímé čáry protínající strany úhlu odříznou proporcionální segmenty ze stran úhlu.

9. Segment rovnoběžný se základnami a procházející bodem průsečíku úhlopříček je těmito základnami rozdělen na polovinu.

7. Známky lichoběžníku

8. Doplňkové konstrukce v lichoběžníku

1. Segment spojující středy stran je středová čára lichoběžníku.

2
. Úsek rovnoběžný s jednou z bočních stran lichoběžníku, jehož jeden konec se shoduje se středem druhé boční strany, druhý patří k přímce obsahující základnu.

3
. Jsou-li uvedeny všechny strany lichoběžníku, vrcholem menší základny se nakreslí přímka rovnoběžná se stranou. Výsledkem je trojúhelník se stranami rovnými bočním stranám lichoběžníku a rozdílem základen. Pomocí Heronova vzorce najděte plochu trojúhelníku a poté výšku trojúhelníku, která se rovná výšce lichoběžníku.

4

. Výška rovnoramenného lichoběžníku, vycházející z vrcholu menší základny, rozděluje větší základnu na segmenty, z nichž jeden se rovná polovině rozdílu základen a druhý polovině součtu základen lichoběžníku, tj. středová čára lichoběžníku.

5. Výšky lichoběžníku, sníženého z vrcholů jedné základny, jsou vyříznuty na přímce obsahující druhou základnu, segment rovný první základně.

6
. Úsek rovnoběžný s jednou z úhlopříček lichoběžníku je prokreslen vrcholem - bodem, který je koncem druhé úhlopříčky. Výsledkem je trojúhelník se dvěma stranami rovnými úhlopříčkám lichoběžníku a třetí rovnou součtu základen

7
.Segment spojující středy úhlopříček se rovná polovině rozdílu základen lichoběžníku.

8. Osy úhlů přiléhajících k jedné z bočních stran lichoběžníku jsou kolmé a protínají se v bodě ležícím na střední čáře lichoběžníku, tj. když se protnou, vznikne pravoúhlý trojúhelník s přeponou rovnou boční strana.

9. Osa lichoběžníkového úhlu odřízne rovnoramenný trojúhelník.

1
0. Úhlopříčky libovolného lichoběžníku, když se protnou, tvoří dva podobné trojúhelníky s koeficientem podobnosti rovným poměru základen a dva stejné trojúhelníky sousedící s bočními stranami.

1
1. Úhlopříčky libovolného lichoběžníku, když se protnou, tvoří dva podobné trojúhelníky s koeficientem podobnosti rovným poměru základen a dva stejné trojúhelníky sousedící s bočními stranami.

1
2. Pokračování stran lichoběžníku k průsečíku umožňuje uvažovat podobné trojúhelníky.

13. Je-li kružnice vepsána do rovnoramenného lichoběžníku, pak vypočítejte výšku lichoběžníku - geometrický průměr součinu základen lichoběžníku nebo dvojnásobek geometrického průměru součinu segmentů boční strany, do které se je rozdělena bodem tečnosti.

9. Oblast lichoběžníku

1 . Plocha lichoběžníku se rovná součinu poloviny součtu základen a výšky S = ½( Pro + A) h nebo

P

Plocha lichoběžníku se rovná součinu střední osy lichoběžníku a jeho výšky S = Pokud je kruh vepsán do lichoběžníku a dotýká se jedné ze stran, rozděluje jej na segmenty h .

2. Plocha lichoběžníku se rovná součinu strany a kolmice nakreslené od středu druhé strany k přímce obsahující první stranu.

Plocha rovnoramenného lichoběžníku s poloměrem vepsané kružnice rovným ra úhel na základněα :

10. Závěr

KDE, JAK A K ČEMU SE LAPÉZ POUŽÍVÁ?

Lichoběžník ve sportu: Lichoběžník je jistě pokrokovým vynálezem lidstva. Je navržen tak, aby ulevil našim rukám a udělal z windsurfingu pohodlný a snadný odpočinek. Chůze na krátkém prkně bez hrazdy nemá vůbec smysl, protože bez ní není možné správně rozložit trakci mezi krok a nohy a efektivně zrychlit.

Lichoběžník v módě: Lichoběžník v oblečení byl populární již ve středověku, v románské době 9.-11. století. Základem ženského oděvu byly tehdy až po zem dlouhé tuniky, tunika se značně rozšiřovala, což vytvářelo lichoběžníkový efekt. K oživení siluety došlo v roce 1961 a stala se hymnou mládí, nezávislosti a kultivovanosti. Obrovskou roli v popularizaci hrazdy sehrála křehká modelka Leslie Hornby, známá jako Twiggy. Nízká dívka s anorektickou postavou a obrovskýma očima se stala symbolem doby a jejím oblíbeným outfitem byly krátké áčkové šaty.

Lichoběžník v přírodě: Lichoběžník se vyskytuje také v přírodě. Lidé mají trapézový sval a někteří lidé mají obličej lichoběžníkového tvaru. Lichoběžníkový tvar mají také okvětní plátky, souhvězdí a samozřejmě hora Kilimandžáro.

Lichoběžník v běžném životě: Lichoběžník se používá i v běžném životě, protože jeho tvar je praktický. Nachází se v takových předmětech, jako jsou: lžíce rypadla, stůl, šroub, stroj.

Lichoběžník je symbolem incké architektury. Dominantní stylistická forma v incké architektuře je jednoduchá, ale půvabná - lichoběžník. Má nejen funkční význam, ale i přísně omezené výtvarné řešení. Lichoběžníkové dveřní otvory, okna a výklenky ve stěnách se nacházejí v budovách všech typů, jak v chrámech, tak v menších budovách, abych tak řekl, hrubší konstrukce. Lichoběžník se nachází i v moderní architektuře. Tato forma budov je neobvyklá, takže takové budovy vždy přitahují oči kolemjdoucích.

Lichoběžník v technologii: Lichoběžník se používá při navrhování dílů v kosmické technice a letectví. Například některé solární panely na vesmírných stanicích mají tvar lichoběžníku, protože mají velkou plochu, což znamená, že akumulují více sluneční energie.

V 21. století už lidé prakticky nepřemýšlejí o významu geometrických tvarů ve svém životě. Vůbec je nezajímá, jaký tvar mají jejich stůl, brýle nebo telefon. Jednoduše volí formu, která je praktická. Ale použití předmětu, jeho účel a výsledek práce mohou záviset na podobě té či oné věci. Dnes jsme vám představili jeden z největších úspěchů lidstva – hrazdu. Otevřeli jsme dveře do nádherného světa postav, řekli jsme vám tajemství lichoběžníku a ukázali vám, že geometrie je všude kolem nás.

Seznam použité literatury

Bolotov A.A., Prokhorenko V.I., Safonov V.F., Matematická teorie a problémy. Kniha 1 Studijní příručka pro uchazeče M.1998 Nakladatelství MPEI.

Bykov A.A., Malyshev G.Yu., Fakulta předuniverzitní přípravy GUVS. Matematika. Vzdělávací a metodická příručka 4 díl M2004

Gordin R.K. Planimetrie. Kniha problémů.

Ivanov A.A. Ivanov A.P., Matematika: Průvodce pro přípravu na Jednotnou státní zkoušku a přijetí na vysoké školy - M: MIPT Publishing House, 2003-288s. ISBN 5-89155-188-3

Pigolkina T.S., Ministerstvo školství a vědy Ruské federace, Federální státní rozpočtová vzdělávací instituce pro další vzdělávání dětí „ZFTSH Moskevský fyzikální a technologický institut (Státní univerzita)“. Matematika. Planimetrie. Úkoly č. 2 pro 10. ročníky (ak. rok 2012-2013).

Pigolkina T.S., Planimetrie (1. část) Matematická encyklopedie účastníka. M., Russian Open University Publishing House 1992.

Sharygin I.F. Vybrané problémy z geometrie pro soutěžní zkoušky na univerzitách (1987-1990) Lvov Magazine „Quantor“ 1991.

Encyklopedie "Avanta Plus", Matematika M., Svět encyklopedií Avanta 2009.

Aplikace

1. Důkaz některých vlastností lichoběžníku.

1. Přímka procházející průsečíkem úhlopříček lichoběžníku rovnoběžná s jeho základnami protíná boční strany lichoběžníku v bodechK A L . Dokažte, že pokud jsou základny lichoběžníku stejné A A A , To délka segmentu KL rovna geometrickému průměru základen lichoběžníku. Důkaz

NechatO - průsečík úhlopříček,INZERÁT = a, slunce = A . Řídit KL rovnoběžně se základnouINZERÁT , tedy,K O║ INZERÁT , trojúhelníkyV K O AŠPATNÝ jsou tedy podobné

(1)

(2)

Dosadíme (2) do (1), dostaneme KO =

Rovněž L.O.= Pak K L = K.O. + L.O. =

V Pro jakýkoli lichoběžník leží střed podstav, průsečík úhlopříček a průsečík pokračování bočních stran na stejné přímce.

Důkaz: Nechte prodloužení stran protínat v boděNA. Skrz bodNA a tečkaO diagonální křižovatkynakreslíme rovnou čáru CO.

Dokažme, že tato přímka rozděluje základy na polovinu.

O významnýVM = x, MS = y, AN = A, ND = proti . máme:

∆ VKM ~ ∆AKN →

∆ MK C ~ ∆NKD → →

Opsaný kruh a lichoběžník. Ahoj! Je tu pro vás ještě jedna publikace, ve které se podíváme na problémy s lichoběžníky. Úlohy jsou součástí zkoušky z matematiky. Zde jsou spojeny do skupiny není dán jen jeden lichoběžník, ale kombinace těles - lichoběžník a kruh. Většina těchto problémů se řeší ústně. Jsou ale i takové, kterým je třeba věnovat zvláštní pozornost, například úkolu 27926.

Jakou teorii si musíte zapamatovat? Tento:

Problémy s lichoběžníky, které jsou dostupné na blogu, si můžete prohlédnout Zde.

27924. Kolem lichoběžníku je popsán kruh. Obvod lichoběžníku je 22, střední čára je 5. Najděte stranu lichoběžníku.

Všimněte si, že kruh lze popsat pouze kolem rovnoramenného lichoběžníku. Je nám dána střední čára, což znamená, že můžeme určit součet základů, to znamená:

To znamená, že součet stran bude roven 22–10=12 (obvod mínus základna). Protože strany rovnoramenného lichoběžníku jsou stejné, jedna strana bude rovna šesti.

27925. Boční strana rovnoramenného lichoběžníku se rovná jeho menší základně, úhel na základně je 60 0, větší základna je 12. Najděte cirkumrádius tohoto lichoběžníku.

Pokud jste vyřešili problémy s kružnicí a šestiúhelníkem vepsaným do ní, pak okamžitě vyslovíte odpověď - poloměr je 6. Proč?

Podívejte se: rovnoramenný lichoběžník se základním úhlem rovným 60 0 a stejnými stranami AD, DC a CB je polovina pravidelného šestiúhelníku:

V takovém šestiúhelníku prochází úsečka spojující protilehlé vrcholy středem kružnice. *Střed šestiúhelníku a střed kruhu se shodují, další podrobnosti

To znamená, že větší základna tohoto lichoběžníku se shoduje s průměrem opsané kružnice. Poloměr je tedy šest.

*Samozřejmě můžeme uvažovat o rovnosti trojúhelníků ADO, DOC a OCB. Dokažte, že jsou rovnostranné. Dále uzavřete, že úhel AOB je roven 180 0 a bod O je stejně vzdálený od vrcholů A, D, C a B, a proto AO=OB=12/2=6.

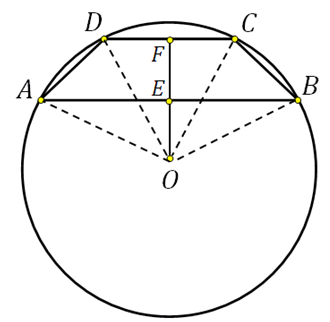
27926. Základny rovnoramenného lichoběžníku jsou 8 a 6. Poloměr kružnice opsané je 5. Najděte výšku lichoběžníku.

Všimněte si, že střed opsané kružnice leží na ose symetrie, a pokud sestrojíme výšku lichoběžníku procházejícího tímto středem, pak když se protne se základnami, rozdělí je na polovinu. Ukážeme si to na náčrtu a také spojíme střed s vrcholy:

Úsek EF je výška lichoběžníku, musíme ho najít.

V pravoúhlém trojúhelníku OFC známe přeponu (to je poloměr kružnice), FC=3 (protože DF=FC). Pomocí Pythagorovy věty můžeme vypočítat OF:

V pravoúhlém trojúhelníku OEB známe přeponu (to je poloměr kružnice), EB=4 (protože AE=EB). Pomocí Pythagorovy věty můžeme vypočítat OE:

Tedy EF=FO+OE=4+3=7.

Nyní důležitá nuance!

V tomto příkladu obrázek jasně ukazuje, že základny leží na opačných stranách středu kruhu, takže problém je vyřešen tímto způsobem.

Co když podmínky neobsahovaly skicu?

Pak by problém měl dvě odpovědi. Proč? Podívejte se pozorně - dva lichoběžníky s danými základnami lze vepsat do libovolného kruhu:

*To znamená, že vzhledem k základnám lichoběžníku a poloměru kruhu existují dva lichoběžníky.

A řešení „druhé možnosti“ bude následující.

Pomocí Pythagorovy věty vypočítáme OF:

Pojďme také vypočítat OE:

Tedy EF=FO–OE=4–3=1.

V problému s krátkou odpovědí na Jednotnou státní zkoušku samozřejmě nemohou být dvě odpovědi a podobný problém se neobejde bez náčrtu. Věnujte proto skice zvláštní pozornost! Totiž: jak jsou umístěny základny lichoběžníku. Ale v úlohách s podrobnou odpovědí to bylo v minulých letech přítomno (s trochu komplikovanější podmínkou). Kdo zvažoval pouze jednu možnost umístění lichoběžníku, ztratil v tomto úkolu bod.

27937. Lichoběžník je opsán kolem kruhu, jehož obvod je 40. Najděte jeho střední čáru.

Zde bychom si měli okamžitě připomenout vlastnost čtyřúhelníku opsaného kolem kruhu:

Součty protilehlých stran kteréhokoli čtyřúhelníku opsaného kružnici jsou stejné.

Zachování vašeho soukromí je pro nás důležité. Z tohoto důvodu jsme vyvinuli Zásady ochrany osobních údajů, které popisují, jak používáme a uchováváme vaše informace. Přečtěte si prosím naše zásady ochrany osobních údajů a dejte nám vědět, pokud máte nějaké dotazy.

Shromažďování a používání osobních údajů

Osobní údaje jsou údaje, které lze použít k identifikaci nebo kontaktování konkrétní osoby.

Kdykoli nás budete kontaktovat, můžete být požádáni o poskytnutí svých osobních údajů.

Níže jsou uvedeny některé příklady typů osobních údajů, které můžeme shromažďovat, a jak takové informace můžeme používat.

Jaké osobní údaje shromažďujeme:

Když odešlete žádost na webu, můžeme shromažďovat různé informace, včetně vašeho jména, telefonního čísla, e-mailové adresy atd.

Jak používáme vaše osobní údaje:

Osobní údaje, které shromažďujeme, nám umožňují kontaktovat vás s jedinečnými nabídkami, akcemi a dalšími událostmi a nadcházejícími událostmi.
Čas od času můžeme použít vaše osobní údaje k zasílání důležitých oznámení a sdělení.
Osobní údaje můžeme také používat pro interní účely, jako je provádění auditů, analýzy dat a různé výzkumy, abychom zlepšili služby, které poskytujeme, a abychom vám poskytli doporučení týkající se našich služeb.
Pokud se účastníte slosování o ceny, soutěže nebo podobné propagační akce, můžeme vámi poskytnuté informace použít ke správě takových programů.

Zpřístupnění informací třetím stranám

Informace, které od vás obdržíme, nesdělujeme třetím stranám.

Výjimky:

Je-li to nutné – v souladu se zákonem, soudním postupem, v soudním řízení a/nebo na základě veřejných žádostí nebo žádostí státních orgánů na území Ruské federace – zveřejnit vaše osobní údaje. Můžeme také zveřejnit informace o vás, pokud usoudíme, že takové zveřejnění je nezbytné nebo vhodné pro účely bezpečnosti, vymáhání práva nebo jiné veřejné důležité účely.
V případě reorganizace, fúze nebo prodeje můžeme osobní údaje, které shromažďujeme, předat příslušné nástupnické třetí straně.

Ochrana osobních údajů

Přijímáme opatření – včetně administrativních, technických a fyzických – k ochraně vašich osobních údajů před ztrátou, krádeží a zneužitím, stejně jako neoprávněným přístupem, zveřejněním, pozměněním a zničením.

Respektování vašeho soukromí na úrovni společnosti

Abychom zajistili, že jsou vaše osobní údaje v bezpečí, sdělujeme našim zaměstnancům standardy ochrany soukromí a zabezpečení a přísně prosazujeme postupy ochrany osobních údajů.

\[(\Velký(\text(Volný lichoběžník)))\]

Definice

Lichoběžník je konvexní čtyřúhelník, ve kterém jsou dvě strany rovnoběžné a další dvě strany nejsou rovnoběžné.

Rovnoběžné strany lichoběžníku se nazývají jeho základny a další dvě strany se nazývají jeho strany.

Výška lichoběžníku je kolmice klesající z libovolného bodu jedné základny k jiné základně.

Věty: vlastnosti lichoběžníku

1) Součet úhlů na straně je \(180^\circ\) .

2) Úhlopříčky rozdělují lichoběžník na čtyři trojúhelníky, z nichž dva jsou podobné a další dva jsou stejně velké.

Důkaz

1) Protože \(AD\paralelní BC\), pak úhly \(\úhel BAD\) a \(\úhel ABC\) jsou pro tyto úsečky jednostranné a příčný \(AB\), proto, \(\úhel BAD +\úhel ABC=180^\circ\).

2) Protože \(AD\paralelní BC\) a \(BD\) jsou sečna, potom \(\úhel DBC=\úhel BDA\) leží napříč.
Také \(\úhel BOC=\úhel AOD\) jako vertikální.
Proto ve dvou úhlech \(\triangle BOC \sim \triangle AOD\).

Pojďme to dokázat \(S_(\trojúhelník AOB)=S_(\trojúhelník COD)\). Nechť \(h\) je výška lichoběžníku. Pak \(S_(\triangle ABD)=\frac12\cdot h\cdot AD=S_(\triangle ACD)\). Pak: \

Definice

Středová čára lichoběžníku je segment spojující středy stran.

Teorém

Středová čára lichoběžníku je rovnoběžná se základnami a rovná se jejich polovičnímu součtu.

Důkaz*

1) Dokažme paralelismus.

Nakreslete bodem \(M\) přímku \(MN"\paralelní AD\) (\(N"\v CD\) ). Pak podle Thalesovy věty (od \(MN"\paralelní AD\paralelní BC, AM=MB\)) bod \(N"\) je středem segmentu \(CD\), což znamená, že body \(N\) a \(N"\) budou shodné.

2) Dokažme vzorec.

Udělejme \(BB"\perp AD, CC"\perp AD\) . Nechat \(BB"\cap MN=M", CC"\cap MN=N"\).

Potom podle Thalesovy věty jsou \(M"\) a \(N"\) středy segmentů \(BB"\) a \(CC"\). To znamená, že \(MM"\) je střední čára \(\triangle ABB"\) , \(NN"\) je střední čára \(\triangle DCC"\) . Proto: \

Protože \(MN\paralelní AD\paralelní BC\) a \(BB", CC"\perp AD\), potom \(B"M"N"C"\) a \(BM"N"C\) jsou obdélníky. Podle Thalesovy věty z \(MN\paralelní AD\) a \(AM=MB\) vyplývá, že \(B"M"=M"B\) . Proto \(B"M"N"C "\) a \(BM"N"C\) jsou stejné obdélníky, proto \(M"N"=B"C"=BC\) .

Tedy:

\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\right)\]

Věta: vlastnost libovolného lichoběžníku

Středy základen, průsečík úhlopříček lichoběžníku a průsečík prodloužení bočních stran leží na stejné přímce.

Důkaz*
Po prostudování tématu „Podobnost trojúhelníků“ se doporučuje seznámit se s důkazem.

1) Dokažme, že body \(P\) , \(N\) a \(M\) leží na stejné přímce.

Nakreslíme přímku \(PN\) (\(P\) je průsečík prodloužení bočních stran, \(N\) je střed \(BC\)). Nechť protíná stranu \(AD\) v bodě \(M\) . Dokažme, že \(M\) je střed \(AD\) .

Zvažte \(\triangle BPN\) a \(\triangle APM\) . Jsou si podobné ve dvou úhlech (\(\úhel APM\) – obecný, \(\úhel PAM=\úhel PBN\) odpovídající v \(AD\paralelní BC\) a \(AB\) sečna). Prostředek: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]

Zvažte \(\triangle CPN\) a \(\triangle DPM\) . Jsou podobné ve dvou úhlech (\(\úhel DPM\) – obecný, \(\úhel PDM=\úhel PCN\) odpovídající v \(AD\paralelní BC\) a \(CD\) sečna). Prostředek: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]

Odtud \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). Ale \(BN=NC\) proto \(AM=DM\) .

2) Dokažme, že body \(N, O, M\) leží na téže přímce.

Nechť \(N\) je střed \(BC\) a \(O\) je průsečík úhlopříček. Nakreslíme přímku \(NE\) , bude protínat stranu \(AD\) v bodě \(M\) . Dokažme, že \(M\) je střed \(AD\) .

\(\triangle BNO\sim \triangle DMO\) podél dvou úhlů (\(\úhel OBN=\úhel ODM\) ležící napříč v \(BC\paralelní AD\) a \(BD\) sečna; \(\úhel BON=\úhel DOM\) jako svislý). Prostředek: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]

Rovněž \(\triangle CON\sim \trojuhelník AOM\). Prostředek: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]

Odtud \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). Ale \(BN=CN\) proto \(AM=MD\) .

\[(\Velký(\text(Rovnoramenný lichoběžník)))\]

Definice

Lichoběžník se nazývá obdélníkový, pokud je jeden z jeho úhlů pravý.

Lichoběžník se nazývá rovnoramenný, pokud jsou jeho strany stejné.

Věty: vlastnosti rovnoramenného lichoběžníku

1) Rovnoramenný lichoběžník má stejné základní úhly.

2) Úhlopříčky rovnoramenného lichoběžníku jsou stejné.

3) Dva trojúhelníky tvořené úhlopříčkami a podstavou jsou rovnoramenné.

Důkaz

1) Uvažujme rovnoramenný lichoběžník \(ABCD\) .

Z vrcholů \(B\) a \(C\) pustíme kolmice \(BM\) a \(CN\) na stranu \(AD\). Protože \(BM\perp AD\) a \(CN\perp AD\) , pak \(BM\paralelní CN\) ; \(AD\paralelní BC\) , pak \(MBCN\) je rovnoběžník, proto \(BM = CN\) .

Uvažujme pravoúhlé trojúhelníky \(ABM\) a \(CDN\) . Protože jejich přepony jsou stejné a noha \(BM\) se rovná noze \(CN\), pak jsou tyto trojúhelníky stejné, tedy \(\úhel DAB = \úhel CDA\) .

Protože \(AB=CD, \úhel A=\úhel D, AD\)- obecný, pak podle prvního znamení. Proto \(AC=BD\) .

3) Protože \(\trojúhelník ABD=\trojúhelník ACD\), pak \(\úhel BDA=\úhel CAD\) . Proto je trojúhelník \(\triangle AOD\) rovnoramenný. Podobně je dokázáno, že \(\trojúhelník BOC\) je rovnoramenný.

Věty: znaky rovnoramenného lichoběžníku

1) Pokud má lichoběžník stejné základní úhly, pak je rovnoramenný.

2) Pokud má lichoběžník stejné úhlopříčky, pak je rovnoramenný.

Důkaz

Uvažujme lichoběžník \(ABCD\) takový, že \(\úhel A = \úhel D\) .

Doplňme lichoběžník na trojúhelník \(AED\), jak je znázorněno na obrázku. Protože \(\úhel 1 = \úhel 2\) , pak je trojúhelník \(AED\) rovnoramenný a \(AE = ED\) . Úhly \(1\) a \(3\) jsou stejné jako odpovídající úhly pro rovnoběžné čáry \(AD\) a \(BC\) a příčné \(AB\). Podobně jsou úhly \(2\) a \(4\) stejné, ale \(\úhel 1 = \úhel 2\), pak \(\úhel 3 = \úhel 1 = \úhel 2 = \úhel 4\), proto je trojúhelník \(BEC\) také rovnoramenný a \(BE = EC\) .

Nakonec \(AB = AE - BE = DE - CE = CD\), tedy \(AB = CD\), což je to, co bylo potřeba dokázat.

2) Nechť \(AC=BD\) . Protože \(\triangle AOD\sim \trojuhelník BOC\), pak jejich koeficient podobnosti označíme jako \(k\) . Pak pokud \(BO=x\) , pak \(OD=kx\) . Podobně jako \(CO=y \Rightarrow AO=ky\) .

Protože \(AC=BD\) , poté \(x+kx=y+ky \Šipka doprava x=y\) . To znamená, že \(\trojúhelník AOD\) je rovnoramenný a \(\úhel OAD=\úhel ODA\) .

Tedy podle prvního znamení \(\trojúhelník ABD=\trojúhelník ACD\) (\(AC=BD, \úhel OAD=\úhel ODA, AD\)– obecné). Takže, \(AB=CD\) , proč.

Lichoběžník je zvláštní případ čtyřúhelníku, ve kterém je jeden pár stran rovnoběžný. Termín „lichoběžník“ pochází z řeckého slova τράπεζα, což znamená „stůl“, „stůl“. V tomto článku se podíváme na typy lichoběžníku a jeho vlastnosti. Navíc vymyslíme, jak vypočítat jednotlivé prvky tohoto Například úhlopříčku rovnoramenného lichoběžníku, středovou čáru, plochu atd. Materiál je prezentován ve stylu elementární oblíbené geometrie, tedy ve snadno dostupné podobě .

Obecné informace

Nejprve si ujasněme, co je čtyřúhelník. Tento obrázek je speciální případ mnohoúhelníku obsahujícího čtyři strany a čtyři vrcholy. Dva vrcholy čtyřúhelníku, které spolu nesousedí, se nazývají opačné. Totéž lze říci o dvou nesousedních stranách. Hlavní typy čtyřúhelníků jsou rovnoběžník, obdélník, kosočtverec, čtverec, lichoběžník a deltoid.

Vraťme se tedy k lichoběžníkům. Jak jsme již řekli, tento obrazec má dvě rovnoběžné strany. Říká se jim báze. Další dvě (neparalelní) jsou boční strany. V materiálech zkoušek a různých testů lze často najít problémy související s lichoběžníky, jejichž řešení často vyžaduje, aby student měl znalosti, které program neposkytuje. Kurz školní geometrie seznamuje studenty s vlastnostmi úhlů a úhlopříček a také se střednicí rovnoramenného lichoběžníku. Ale kromě toho má zmíněný geometrický obrazec další rysy. Ale více o nich o něco později...

Typy lichoběžníku

Existuje mnoho typů tohoto obrázku. Nejčastěji je však obvyklé uvažovat o dvou z nich - rovnoramenném a obdélníkovém.

1. Obdélníkový lichoběžník je obrazec, jehož jedna ze stran je kolmá k základnám. Její dva úhly se vždy rovnají devadesáti stupňům.

2. Rovnoramenný lichoběžník je geometrický útvar, jehož strany jsou si navzájem rovné. To znamená, že úhly na základnách jsou stejné i ve dvojicích.

Hlavní principy metodiky studia vlastností lichoběžníku

Mezi hlavní princip patří využití tzv. úkolového přístupu. Ve skutečnosti není třeba zavádět nové vlastnosti tohoto útvaru do teoretického kurzu geometrie. Mohou být objeveny a formulovány v procesu řešení různých problémů (nejlépe systémových). Zároveň je velmi důležité, aby učitel věděl, jaké úkoly je třeba studentům v tu či onu dobu v průběhu vzdělávacího procesu zadávat. Navíc každá vlastnost lichoběžníku může být reprezentována jako klíčová úloha v systému úloh.

Druhým principem je tzv. spirálová organizace studia „pozoruhodných“ vlastností lichoběžníku. To znamená návrat během procesu učení k jednotlivým rysům daného geometrického útvaru. Studenti si je tak snáze zapamatují. Například vlastnost čtyř bodů. Lze to prokázat jak při studiu podobnosti, tak následně pomocí vektorů. A ekvivalenci trojúhelníků sousedících s bočními stranami obrazce lze dokázat použitím nejen vlastností trojúhelníků se stejnou výškou nakreslených na strany, které leží na stejné přímce, ale také pomocí vzorce S = 1/2( ab*sinα). Kromě toho můžete pracovat na vepsaném lichoběžníku nebo pravoúhlém trojúhelníku na vepsaném lichoběžníku atd.

Využití „mimoškolních“ prvků geometrického útvaru v obsahu školního kurzu je technologií pro jejich výuku založenou na úkolech. Neustálé odkazování na studované vlastnosti při procházení dalších témat umožňuje studentům získat hlubší znalosti o lichoběžníku a zajišťuje úspěšnost řešení zadaných problémů. Začněme tedy studovat tuto nádhernou postavu.

Prvky a vlastnosti rovnoramenného lichoběžníku

Jak jsme již uvedli, tento geometrický obrazec má stejné strany. Je také známý jako správný lichoběžník. Proč je tak pozoruhodný a proč získal takové jméno? Zvláštností tohoto obrázku je, že nejen strany a úhly na základnách jsou stejné, ale také úhlopříčky. Navíc součet úhlů rovnoramenného lichoběžníku je 360 stupňů. Ale to není všechno! Ze všech známých lichoběžníků lze jako kruh označit pouze rovnoramenný. To je způsobeno skutečností, že součet opačných úhlů tohoto obrázku je roven 180 stupňům a pouze za této podmínky lze popsat kruh kolem čtyřúhelníku. Další vlastností uvažovaného geometrického útvaru je, že vzdálenost od vrcholu základny k průmětu opačného vrcholu na přímku, která obsahuje tuto základnu, bude rovna středové čáře.

Nyní pojďme zjistit, jak najít úhly rovnoramenného lichoběžníku. Zvažme řešení tohoto problému za předpokladu, že jsou známy rozměry stran obrázku.

Řešení

Typicky se čtyřúhelník obvykle označuje písmeny A, B, C, D, kde BS a AD jsou základny. V rovnoramenném lichoběžníku jsou strany stejné. Budeme předpokládat, že jejich velikost je rovna X a velikosti základen jsou rovna Y a Z (menší a větší). K provedení výpočtu je nutné nakreslit výšku H z úhlu B. Výsledkem je pravoúhlý trojúhelník ABN, kde AB je přepona a BN a AN jsou nohy. Vypočítáme velikost nohy AN: menší odečteme od větší základny a výsledek vydělíme 2. Zapíšeme jej ve tvaru vzorce: (Z-Y)/2 = F. Nyní pro výpočet akutní úhlu trojúhelníku, použijeme funkci cos. Dostaneme následující záznam: cos(β) = X/F. Nyní vypočítáme úhel: β=arcos (X/F). Dále, když známe jeden úhel, můžeme určit druhý, k tomu provedeme elementární aritmetickou operaci: 180 - β. Všechny úhly jsou definovány.

Existuje druhé řešení tohoto problému. Nejprve ji spustíme z rohu do výšky H. Vypočteme hodnotu nohy BN. Víme, že druhá mocnina přepony pravoúhlého trojúhelníku se rovná součtu čtverců nohou. Dostaneme: BN = √(X2-F2). Dále použijeme goniometrickou funkci tg. Výsledkem je: β = arctan (BN/F). Byl nalezen ostrý úhel. Dále jej definujeme podobně jako u prvního způsobu.

Vlastnost úhlopříček rovnoramenného lichoběžníku

Nejprve si sepišme čtyři pravidla. Pokud jsou úhlopříčky v rovnoramenném lichoběžníku kolmé, pak:

Výška postavy bude rovna součtu základen děleno dvěma;

Jeho výška a středová čára jsou stejné;

Střed kruhu je bod, ve kterém ;

Pokud je boční strana rozdělena bodem tečnosti na segmenty H a M, pak se rovná druhé odmocnině součinu těchto segmentů;

Čtyřúhelník, který je tvořen tečnými body, vrcholem lichoběžníku a středem vepsané kružnice, je čtverec, jehož strana je rovna poloměru;

Plocha obrázku se rovná součinu základen a součinu poloviny součtu základen a její výšky.

Podobné lichoběžníky

Toto téma je velmi vhodné pro studium vlastností tohoto Například úhlopříčky rozdělují lichoběžník na čtyři trojúhelníky a ty, které sousedí se základnami, jsou podobné, a ty, které sousedí se stranami, jsou stejně velké. Toto tvrzení lze nazvat vlastností trojúhelníků, na které je lichoběžník rozdělen svými úhlopříčkami. První část tohoto tvrzení je dokázána pomocí znaku podobnosti ve dvou úhlech. K prokázání druhé části je lepší použít metodu uvedenou níže.

Důkaz věty

Akceptujeme, že obrazec ABSD (AD a BS jsou základny lichoběžníku) je rozdělen úhlopříčkami VD a AC. Jejich průsečík je O. Dostaneme čtyři trojúhelníky: AOS - na spodní základně, BOS - na horní základně, ABO a SOD po stranách. Trojúhelníky SOD a BOS mají společnou výšku, pokud jsou segmenty BO a OD jejich základnami. Zjistíme, že rozdíl mezi jejich plochami (P) je roven rozdílu mezi těmito segmenty: PBOS/PSOD = BO/OD = K. Proto PSOD = PBOS/K. Podobně trojúhelníky BOS a AOB mají společnou výšku. Za jejich základny bereme segmenty CO a OA. Dostaneme PBOS/PAOB = CO/OA = K a PAOB = PBOS/K. Z toho vyplývá, že PSOD = PAOB.

Pro upevnění látky se studentům doporučuje najít souvislost mezi oblastmi výsledných trojúhelníků, na které je lichoběžník svými úhlopříčkami rozdělen, řešením následující úlohy. Je známo, že trojúhelníky BOS a AOD mají stejné plochy, je nutné najít oblast lichoběžníku. Protože PSOD = PAOB, znamená to PABSD = PBOS+PAOD+2*PSOD. Z podobnosti trojúhelníků BOS a AOD vyplývá, že BO/OD = √(PBOS/PAOD). Proto PBOS/PSOD = BO/OD = √(PBOS/PAOD). Dostaneme PSOD = √(PBOS*PAOD). Potom PABSD = PBOS+PAOD+2*√(PBOS*PAOD) = (√PBOS+√PAOD)2.

Vlastnosti podobnosti

Při dalším rozvíjení tohoto tématu můžeme prokázat další zajímavé vlastnosti lichoběžníků. Pomocí podobnosti lze tedy dokázat vlastnost úsečky, která prochází bodem tvořeným průsečíkem úhlopříček tohoto geometrického útvaru rovnoběžně se základnami. K tomu vyřešme následující problém: je nutné najít délku úsečky RK, která prochází bodem O. Z podobnosti trojúhelníků AOD a BOS vyplývá, že AO/OS = AD/BS. Z podobnosti trojúhelníků AOP a ASB vyplývá, že AO/AC=RO/BS=AD/(BS+AD). Odtud dostaneme, že RO=BS*BP/(BS+BP). Podobně z podobnosti trojúhelníků DOC a DBS vyplývá, že OK = BS*AD/(BS+AD). Odtud dostaneme, že RO=OK a RK=2*BS*AD/(BS+AD). Segment procházející průsečíkem úhlopříček, rovnoběžný se základnami a spojující dvě boční strany, je rozdělen na polovinu průsečíkem. Jeho délka je harmonickým průměrem podstav figury.

Uvažujme následující vlastnost lichoběžníku, která se nazývá vlastnost čtyř bodů. Průsečíky úhlopříček (O), průsečík pokračování stran (E) a také středy základen (T a F) leží vždy na stejné přímce. To lze snadno dokázat pomocí podobnostní metody. Výsledné trojúhelníky BES a AED jsou podobné a v každém z nich mediány ET a EJ rozdělují vrcholový úhel E na stejné části. Body E, T a F tedy leží na stejné přímce. Stejným způsobem jsou body T, O a Zh umístěny na stejné přímce To vše vyplývá z podobnosti trojúhelníků BOS a AOD. Odtud usuzujeme, že všechny čtyři body – E, T, O a F – budou ležet na stejné přímce.

Pomocí podobných lichoběžníků můžete požádat studenty, aby našli délku segmentu (LS), který rozděluje obrazec na dva podobné. Tento segment musí být rovnoběžný se základnami. Protože výsledné lichoběžníky ALFD a LBSF jsou podobné, pak BS/LF = LF/AD. Z toho vyplývá, že LF=√(BS*AD). Zjistíme, že úsečka rozdělující lichoběžník na dva podobné má délku rovnou geometrickému průměru délek základen obrazce.

Zvažte následující podobnostní vlastnost. Je založen na segmentu, který rozděluje lichoběžník na dvě stejné postavy. Předpokládáme, že lichoběžník ABSD je rozdělen segmentem EH na dva podobné. Z vrcholu B je vynechána výška, která je segmentem EN rozdělena na dvě části - B1 a B2. Dostaneme: PABSD/2 = (BS+EN)*B1/2 = (AD+EN)*B2/2 a PABSD = (BS+AD)*(B1+B2)/2. Dále sestavíme systém, jehož první rovnice je (BS+EN)*B1 = (AD+EN)*B2 a druhá (BS+EN)*B1 = (BS+AD)*(B1+B2)/2. Z toho vyplývá, že B2/B1 = (BS+EN)/(AD+EN) a BS+EN = ((BS+AD)/2)*(1+B2/B1). Zjistíme, že délka úsečky rozdělující lichoběžník na dva stejné lichoběžníky je rovna střední druhé mocnině délek základen: √((BS2+AD2)/2).

Zjištění podobnosti

Dokázali jsme tedy, že:

1. Úsek spojující středy bočních stran lichoběžníku je rovnoběžný s AD a BS a je roven aritmetickému průměru BS a AD (délka základny lichoběžníku).

2. Přímka procházející bodem O průsečíku úhlopříček rovnoběžných s AD a BS bude rovna harmonickému průměru čísel AD a BS (2*BS*AD/(BS+AD)).

3. Úsek rozdělující lichoběžník na podobné má délku geometrického průměru základen BS a AD.

4. Prvek rozdělující obrazec na dva stejné má délku střední odmocniny čísel AD a BS.

Pro upevnění materiálu a pochopení souvislostí mezi uvažovanými segmenty je student potřebuje sestrojit pro konkrétní lichoběžník. Dokáže snadno zobrazit střední čáru a segment, který prochází bodem O - průsečíkem úhlopříček obrazce - rovnoběžně se základnami. Kde se ale bude nacházet třetí a čtvrtý? Tato odpověď přivede žáka k objevení žádoucího vztahu mezi průměrnými hodnotami.

Segment spojující středy úhlopříček lichoběžníku

Zvažte následující vlastnost tohoto obrázku. Předpokládáme, že úsečka MH je rovnoběžná se základnami a půlí úhlopříčky. Nazvěme průsečíky Ш a Ш. Tento segment bude roven polovině rozdílu základen. Podívejme se na to podrobněji. MS je střední čára ABS trojúhelníku, rovná se BS/2. MSH je střední čára trojúhelníku ABD, rovná se AD/2. Pak dostaneme, že ShShch = MSh-MSh, tedy ShShch = AD/2-BS/2 = (AD+VS)/2.

Těžiště

Podívejme se, jak je tento prvek určen pro daný geometrický obrazec. K tomu je nutné prodloužit základny v opačných směrech. co to znamená? K horní základně musíte přidat spodní základnu - v libovolném směru, například vpravo. A spodní prodloužíme o délku horního doleva. Dále je spojíme diagonálně. Průsečík tohoto segmentu se střední osou obrázku je těžištěm lichoběžníku.

Lichoběžníky vepsané a opsané

Pojďme si vyjmenovat vlastnosti takových postav:

1. Lichoběžník lze vepsat do kruhu pouze tehdy, je-li rovnoramenný.

2. Lichoběžník lze popsat kolem kruhu za předpokladu, že součet délek jejich základen je roven součtu délek stran.

Důsledky incircle:

1. Výška popisovaného lichoběžníku je vždy rovna dvěma poloměrům.

2. Strana popisovaného lichoběžníku je pozorována ze středu kružnice v pravém úhlu.

První důsledek je zřejmý, ale k prokázání druhého je nutné zjistit, že úhel SOD je správný, což ve skutečnosti také není obtížné. Ale znalost této vlastnosti vám umožní používat při řešení problémů pravoúhlý trojúhelník.

Nyní upřesněme tyto důsledky pro rovnoramenný lichoběžník vepsaný do kruhu. Zjistíme, že výška je geometrickým průměrem základen obrázku: H=2R=√(BS*AD). Při nácviku základní techniky řešení úloh pro lichoběžníky (princip kreslení dvou výšek) musí student vyřešit následující úlohu. Předpokládáme, že BT je výška rovnoramenného obrazce ABSD. Je nutné najít segmenty AT a TD. Pomocí výše popsaného vzorce to nebude těžké.

Nyní pojďme zjistit, jak určit poloměr kruhu pomocí oblasti opsaného lichoběžníku. Snižujeme výšku od vrcholu B k základně AD. Protože je kružnice vepsána do lichoběžníku, pak BS+AD = 2AB nebo AB = (BS+AD)/2. Z trojúhelníku ABN najdeme sinα = BN/AB = 2*BN/(BS+AD). PABSD = (BS+BP)*BN/2, BN=2R. Dostaneme PABSD = (BS+BP)*R, z toho vyplývá, že R = PABSD/(BS+BP).