معادلات درجه دوم و نابرابری با یک پارامتر. کتاب درسی معادلات و نامساوی با پارامترها معادلات خطی و نامساوی با پارامترها
در این درس الگوریتم حل نابرابری ها با پارامترها را مطالعه می کنیم و یاد می گیریم که چگونه در حل این نوع مسائل از آن استفاده کنیم.
تعریف یک.
حل یک نابرابری با یک پارامتر به معنای یافتن مجموعه تمام راه حل های یک نابرابری معین یا اثبات عدم وجود راه حل برای هر مقدار پارامتر است.
بیایید نابرابری های خطی را در نظر بگیریم.
تعریف دو.
نابرابری های شکل a x به علاوه بزرگتر از صفر، بزرگتر یا مساوی صفر، کوچکتر از صفر، کوچکتر یا مساوی صفر باشند، جایی که الفو be اعداد واقعی هستند، X- متغیرها را نابرابری های درجه اول (نابرابری های خطی) می گویند.
الگوریتمی برای حل یک نابرابری خطی با یک پارامتر، به عنوان مثال، نامعادله x به علاوه بزرگتر از صفر باشد، که در آن الفو be اعداد واقعی هستند، X- متغیر موارد زیر را در نظر بگیرید:
مورد اول:الفبزرگتر از صفر است، سپس x بزرگتر از منهای تقسیم بر a است.
در نتیجه، مجموعه راه‌حل‌های نابرابری یک پرتو عددی باز است که از منهای بر یک به اضافه بینهایت تقسیم می‌شود.
مورد دوم:الفکمتر از صفر است، سپس x کمتر از منهای تقسیم بر a است
و بنابراین، مجموعه راه حل های نابرابری یک پرتو عددی باز از منهای بی نهایت به منهای است که بر a تقسیم می شود.
مورد سوم: الفبرابر با صفر است، سپس نابرابری به شکل زیر در می آید: صفر ضرب در x به علاوه بزرگتر از صفر باشد و برای بائهبزرگتر از صفر، هر عدد واقعی راه حلی برای نابرابری است، و چه زمانی بائهکمتر یا مساوی صفر، نابرابری راه حلی ندارد.
نابرابری های باقی مانده نیز به همین ترتیب حل می شوند.
بیایید به نمونه هایی نگاه کنیم.
وظیفه 1
حل نامعادله a x کوچکتر یا مساوی یک است.
راه حل
بسته به علامت الفبیایید سه مورد را در نظر بگیریم.
مورد اول: اگر الفبزرگتر از صفر است، سپس x کوچکتر یا مساوی یک تقسیم بر a است.
حالت دوم: اگر الفکوچکتر از صفر است، سپس x بزرگتر یا مساوی یک تقسیم بر a است.
مورد سوم: اگر الفبرابر با صفر است، سپس نابرابری به شکل زیر در می آید: صفر ضرب در x کوچکتر یا مساوی یک است و بنابراین، هر عدد واقعی راه حلی برای نامساوی اصلی است.
بنابراین، اگر الفبزرگتر از صفر است، سپس x متعلق به پرتو از منهای بی نهایت تا یک تقسیم بر a است.
اگر الف الفبرابر با صفر،
که x
پاسخ: اگر الفبزرگتر از صفر است، سپس x متعلق به پرتو از منهای بی نهایت تا یک تقسیم بر a است.
اگر الفکوچکتر از صفر است، پس x متعلق به پرتو یک تقسیم بر a به اضافه بی نهایت است، و اگر الفبرابر با صفر،
که x x متعلق به مجموعه اعداد حقیقی است.
وظیفه 2
ماژول نابرابری x منهای دو بزرگتر از منهای مربع اختلاف بین a و یک را حل کنید.
راه حل
توجه داشته باشید که مدول x منهای دو برای هر واقعی بزرگتر یا مساوی صفر است Xو منهای مجذور اختلاف بین a و یک برای هر مقدار از پارامتر، کمتر یا مساوی صفر است الف. بنابراین، اگر الفبرابر یک، سپس هر X- عدد حقیقی غیر از دو راه حلی برای نابرابری است و اگر الفبرابر یک نیست، پس هر عدد واقعی راه حلی برای نابرابری است.
پاسخ: اگر الفبرابر یک است، سپس x متعلق به اتحاد دو پرتو عدد باز از منهای بینهایت به دو و از دو به مثبت بی نهایت است،
چه می شود اگر الفمتعلق به اتحاد دو پرتو عدد باز از منهای بی نهایت به یک و از یک به مثبت بی نهایت است، سپس Xمتعلق به مجموعه اعداد حقیقی است.
وظیفه 3
نابرابری را سه برابر اختلاف چهار a و x کوچکتر از دو a x به اضافه سه حل کنید.
راه حل
پس از تبدیل های ابتدایی این نابرابری، نابرابری را به دست می آوریم: x ضرب در مجموع دو a و سه بزرگتر از سه ضرب در اختلاف چهار a و یک است.
حالت اول: اگر دو a به علاوه سه بزرگتر از صفر باشد، یعنی الفبزرگتر از منهای سه ثانیه است، سپس x بزرگتر از کسری است که صورت آن سه برابر اختلاف چهار a و یک است و مخرج آن دو a به علاوه سه است.
حالت دوم: اگر دو a به علاوه سه کمتر از صفر باشد، یعنی الفکمتر از منهای سه ثانیه است، سپس x کوچکتر از کسری است که صورت آن سه برابر اختلاف چهار a و یک و مخرج آن دو a به علاوه سه است.
حالت سوم: اگر دو a به علاوه سه برابر با صفر باشد، یعنی الفبرابر منهای سه ثانیه،
هر عدد واقعی راه حلی برای نابرابری اصلی است.
در نتیجه، اگر a متعلق به خط اعداد باز از منهای سه ثانیه تا به علاوه بی نهایت باشد، آنگاه x
متعلق به یک خط اعداد باز از کسری است که صورت آن سه برابر اختلاف چهار a و یک و مخرج آن دو a به علاوه سه به اضافه بی نهایت است.
اگر a متعلق به خط اعداد باز از منهای بینهایت تا منهای سه ثانیه باشد، x متعلق به خط اعداد باز از منهای بینهایت به کسری است که صورت آن سه برابر اختلاف چهار a و یک و مخرج آن دو a مثبت است. سه
اگر الفپس برابر با منهای سه ثانیه است Xمتعلق به مجموعه اعداد حقیقی است.
پاسخ: اگر a متعلق به خط اعداد باز از منهای سه ثانیه تا مثبت بی نهایت باشد، آنگاه x
متعلق به یک پرتو عدد باز از کسری است که صورت آن سه برابر اختلاف چهار a و یک و مخرج آن دو a به علاوه سه به اضافه بی نهایت است.
اگر a متعلق به خط اعداد باز از منهای بینهایت تا منهای سه ثانیه باشد، x متعلق به خط اعداد باز از منهای بینهایت به کسری است که صورت آن سه برابر اختلاف چهار a و یک است و مخرج آن دو a مثبت است. سه
اگر الفپس برابر با منهای سه ثانیه است Xمتعلق به مجموعه اعداد حقیقی است.
وظیفه 4
برای همه مقادیر پارامتر معتبر الفنابرابری جذر x منهای یک جذر مثبت دو منهای x به علاوه جذر منهای یک به علاوه جذر سه منهای a بالای صفر را حل کنید.
راه حل
بیایید دامنه تعریف پارامتر را پیدا کنیم الف. توسط سیستمی از نابرابری ها تعیین می شود که با حل آن متوجه می شویم که a متعلق به بخش یک تا سه است.
این نابرابری معادل سیستمی از نابرابری ها است که با حل آن متوجه می شویم که x متعلق به بخش a تا دو a است.
اگر a متعلق به بخش یک تا سه باشد، راه‌حل نابرابری اصلی، پاره از a تا دو a است.
پاسخ: اگر a متعلق به قطعه یک تا سه باشد، toix متعلق به قطعه a تا دو a است.
وظیفه 5
پیدا کردن همه الف، برای کدام نابرابری
جذر x مجذور منهای x منهای دو به اضافه جذر کسری که صورت آن دو منهای x است و مخرج آن x به اضافه چهار بزرگتر یا مساوی با x به اضافه دو منهای جذر کسری است که رقم آن x به علاوه یک و مخرج پنج منهای x هیچ راه حلی ندارد.
راه حل
اول اجازه دهید دامنه تعریف این نابرابری را محاسبه کنیم. توسط سیستمی از نامساوی که راه حل آن دو عدد است تعیین می شود: x برابر با منهای یک و x برابر با دو است.
دوم بیایید تمام مقادیر a را که این نابرابری برای آنها راه حل دارد، پیدا کنیم. ما برای این همه چیز پیدا خواهیم کرد الف، که x برابر با منهای یک و x برابر با دو است - این راه حل این نابرابری است. اجازه دهید مجموعه ای از دو سیستم را در نظر بگیریم و حل کنیم. راه حل این است که دو پرتو عددی را از منهای بی نهایت تا منهای یک نصف و از یک به مثبت بی نهایت ترکیب کنیم.
این به این معنی است که اگر a متعلق به اتحاد دو پرتو عددی منهای باشد، این نابرابری راه حل دارد.
بینهایت تا منهای یک نیمه و از یک به اضافه بی نهایت.
سوم در نتیجه، اگر a متعلق به بازه منهای یک نصف تا یک باشد، این نابرابری راه حلی ندارد.
پاسخ: اگر a به بازه منهای یک نصف تا یک تعلق داشته باشد، نابرابری راه حلی ندارد.
حل نابرابری ها با یک پارامتر
نامساوی هایی که به شکل ax > b، ax هستند< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются نابرابری های خطی.
اصول حل نابرابری های خطی با پارامتر بسیار شبیه به اصول حل معادلات خطی با پارامتر است.
مثال 1.
حل نابرابری 5x – a > تبر + 3.
راه حل.
ابتدا بیایید نابرابری اصلی را تبدیل کنیم:
5x – ax > a + 3، بیایید x را در سمت چپ نابرابری خارج از پرانتز قرار دهیم:
(5 – a)x > a + 3. حال موارد ممکن را برای پارامتر a در نظر بگیرید:
اگر a > 5، آنگاه x< (а + 3) / (5 – а).
اگر a = 5 باشد، هیچ راه حلی وجود ندارد.
اگر الف< 5, то x >(a + 3) / (5 - a).
این راه حل پاسخی به نابرابری خواهد بود.
مثال 2.
نابرابری x(a – 2) / (a – 1) – 2a/3 ≤ 2x – a را برای a ≠ 1 حل کنید.
راه حل.
بیایید نابرابری اصلی را تبدیل کنیم:
x(a – 2) / (a – 1) – 2x ≤ 2a/3 – a;
Ах/(а – 1) ≤ -а/3. با ضرب دو طرف نابرابری در (-1) به دست می آید:
ax/(a – 1) ≥ a/3. اجازه دهید موارد ممکن برای پارامتر a را بررسی کنیم:
1 مورد.
بگذارید a/(a – 1) > 0 یا a € (-∞; 0)ᴗ(1; +∞). سپس x ≥ (a – 1)/3.
مورد 2.< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.
اجازه دهید a/(a – 1) = 0، یعنی. a = 0. سپس x هر عدد واقعی است.
مورد 3.
بگذارید a/(a – 1)
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] برای € (0; 1)؛
راه حل.
x € R برای a = 0.
مثال 3.
حل نابرابری |1 + x| ≤ تبر نسبت به x.
از این شرط نتیجه می شود که سمت راست محور نابرابری باید غیر منفی باشد، یعنی. تبر ≥ 0. با قانون آشکار شدن ماژول از نابرابری |1 + x| ≤ تبر یک نابرابری مضاعف داریم
تبر ≤ 1 + x ≤ تبر. بیایید نتیجه را در قالب یک سیستم بازنویسی کنیم:
(تبر ≥ 1 + x;
(-ax ≤ 1 + x.
بیایید آن را به: ((a – 1)x ≥ 1;:
((a + 1)x ≥ -1.
ما سیستم به دست آمده را در فواصل و در نقاط مطالعه می کنیم< а < 0 x € [-1/(а – 1); 1/(а – 1)].
(شکل 1)
برای ≤ -1 x € (-∞؛ 1/(a – 1)].< а ≤ 1 решений нет.
در -1
وقتی a = 0 x = -1.
در 0
مثال 1.
روش گرافیکی برای حل نابرابری ها< bx.
راه حل.
رسم نمودارها حل معادلات حاوی یک پارامتر را بسیار ساده می کند. استفاده از روش گرافیکی هنگام حل نابرابری ها با یک پارامتر حتی واضح تر و مصلحت تر است. حل گرافیکی نابرابری های فرم f(x) ≥ g(x) به معنای یافتن مقادیر متغیر x است که نمودار تابع f(x) بالای نمودار تابع g(x) قرار دارد. برای انجام این کار، همیشه لازم است نقاط تقاطع نمودارها را (در صورت وجود) پیدا کنید.حل نابرابری |x + 5| 
ما نمودارهایی از توابع y = |x + 5| می سازیم و y = bx
(شکل 2)
. راه حل نابرابری آن مقادیری از متغیر x خواهد بود که نمودار تابع y = |x + 5| زیر نمودار تابع y = bx خواهد بود.< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).
تصویر نشان می دهد:
4) برای 0 ≤ b ≤ 1، نمودارها قطع نمی شوند، به این معنی که نابرابری هیچ راه حلی ندارد.
پاسخ: x € (-∞؛ 5/(b – 1)) برای b ≤ -1.
x € (-5/(b + 1)؛ 5/(b – 1)) در -1< b < 0;
هیچ راه حلی برای 0 ≤ b ≤ 1 وجود ندارد. x € (5/(b – 1)؛ +∞) برای b > 1.
مثال 2.
نابرابری a(a + 1)x > (a + 1) (a + 4) را حل کنید.
راه حل.
1) بیایید مقادیر "کنترل" را برای پارامتر a پیدا کنیم: a 1 = 0 و 2 = -1.
2) بیایید این نابرابری را در هر زیر مجموعه از اعداد حقیقی حل کنیم: (-∞; -1)؛ (-1)؛ (-1; 0); (0)؛ (0؛ +∞).
الف) الف< -1, из данного неравенства следует, что х >(a + 4)/a;
ب) a = -1، سپس این نابرابری به شکل 0 x > 0 خواهد بود - هیچ راه حلی وجود ندارد.
ج) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;
د) a = 0، سپس این نابرابری به شکل 0 x > 4 است - هیچ راه حلی وجود ندارد.
ه) a > 0، از این نابرابری نتیجه می شود که x > (a + 4)/a.
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞);
حل نابرابری |2 – |x||< a – x.
راه حل.
یک نمودار از تابع y = |2 – |x|| می سازیم (شکل 3)و تمام موارد ممکن از محل خط راست y = -x + a را در نظر بگیرید. 
پاسخ: نابرابری هیچ راه حلی برای ≤ -2 ندارد.
x € (-∞؛ (a – 2)/2) برای € (-2; 2];
x € (-∞؛ (a + 2)/2) برای a > 2.
هنگام حل مسائل مختلف، معادلات و نابرابری ها با پارامترها، تعداد قابل توجهی از تکنیک های اکتشافی کشف می شوند که می توانند با موفقیت در هر شاخه دیگری از ریاضیات به کار روند.
مسائل مربوط به پارامترها نقش مهمی در شکل گیری تفکر منطقی و فرهنگ ریاضی دارند. به همین دلیل است که با تسلط بر روش های حل مسائل با پارامترها، با موفقیت با سایر مشکلات کنار می آیید.
هنوز سوالی دارید؟ نمی دانید چگونه نابرابری ها را حل کنید؟
برای کمک گرفتن از استاد راهنما، ثبت نام کنید.
درس اول رایگان است
وب سایت، هنگام کپی کردن مطالب به طور کامل یا جزئی، پیوند به منبع مورد نیاز است.
سری "آموزش حل مسائل با پارامترها"
IV. معادلات درجه دوم و نابرابری با پارامتر
IV.1. مفاهیم اساسی
تعریف. تابعی از فرم (1)، که در آن، توابع داده شده پارامتر هستند الف، که در تقاطع دامنه های تعریف آنها در نظر گرفته می شود، یک تابع درجه دوم با پارامتر نامیده می شود. الف.
نمونه ها
1. .
2. .
3. .
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
تعریف. زیر دامنه تعریف تابع درجه دوم (1) با پارامتر الفما کل مجموعه جفت مقادیر را درک خواهیم کرد Xو الفنوع ( X; الف) که برای هر یک از آنها عبارت معنای خود را از دست نمی دهد.
اجازه دهید دامنه های تعریف توابع 1-10 را ایجاد کنیم.
1. 2.
3. 4. 5.
6. 7. 8. 9. 10.
اگر پارامتر یکی از مقادیر عددی را بگیرد، تابع (1) به شکل یکی از توابع با ضرایب عددی خواهد بود:
;
;
;
;
;
;
,
کجا ک, ب, ج- اعداد واقعی
اجازه دهید به این واقعیت توجه کنیم که برای برخی از مقادیر پارامتر از، یک تابع درجه دوم با یک پارامتر به شکل یک تابع درجه دوم بدون پارامتر یا یک تابع خطی است.
از آنجایی که یک تابع درجه دوم با یک پارامتر اغلب خانواده ای از توابع درجه دوم یا خطی را با ضرایب عددی "تولید" می کند، پس صحبت از نمودارهای یک تابع درجه دوم با یک پارامتر، منظور ما نمودارهای زیادی از این خانواده خواهد بود.
تعریف. الفمعادله ای از فرم (1) نامیده می شود که در آن، , این توابع پارامتر هستند الف، در تقاطع دامنه های تعریف آنها در نظر گرفته شده است.
به طور خاص، برخی از ضرایب یا عبارت رهگیری ممکن است اعداد باشند.
نمونه ها
, (1)
,
(2)
, (3)
, (4)
. (5)
با استفاده از تعریف یک تابع درجه دوم با یک پارامتر، می توانیم تعریف زیر را از یک معادله درجه دوم با یک پارامتر ارائه دهیم.
تعریف. معادله درجه دوم با پارامتر الفمعادله ای از فرم نامیده می شود که در آن یک تابع درجه دوم با پارامتر وجود دارد الف.
اگر، پس معادله (1) به معنای سنتی درجه دوم است، یعنی. درجه دوم
اگر، معادله (1) خطی می شود.
برای همه مقادیر پارامتر معتبر الف، که و با استفاده از فرمول های شناخته شده، عباراتی را برای ریشه های معادله (1) بر حسب پارامتر بدست می آوریم.
آن ارزش ها الف، که در آن، باید جداگانه به عنوان موارد خاص در نظر گرفته شود.
بنابراین، برای مثال، معادله (5) at به شکل .
IV.2. معادلات درجه دوم با پارامتر
№1. معادله را حل کنید.
- معادله-نتیجه. دریافت می کنیم: , .
در سیستم مختصات ( اوه) راه حل را کامل می کنیم. (شکل 1)
پاسخ: 1. اگر , پس .
2. اگر، پس.
3. اگر، پس، .
№2. مقدار پارامتر را پیدا کنید الف، که در آن معادله یک ریشه دارد. اگر چندین مقدار از این قبیل وجود دارد، مجموع آنها را در پاسخ خود بنویسید.
این معادله به یک سیستم معادل کاهش می یابد:
بیایید آن را به شکل: و به صورت گرافیکی در سیستم مختصات حل کنیم ( xOa). (شکل 2).
معادله دارای یک ریشه در , و .
№3. همه مقادیر را پیدا کنید Xبه طوری که برای هر مقدار از پارامتر الف، به بازه (0; 2] تعلق ندارد، عبارت برابر با عبارت نیست. (USE-2007).
بیایید مشکل را دوباره فرمول بندی کنیم: «همه مقادیر را پیدا کنید Xبه طوری که برای هر مقدار از پارامتر معادله 
ریشه ندارد."
بیان کنیم الفاز طریق X:
1) اجازه دهید. سپس . بنابراین معادله دارای ریشه است. این بدان معنی است که شرایط را برآورده نمی کند.
2) اجازه دهید. سپس . بیایید از سیستم مختصات استفاده کنیم ( xOa). (شکل 3).
شرط ارضا شده است.
№4. بسته به پارامتر چند ریشه دارد الفمعادله دارد؟
بیایید ماژول را گسترش دهیم:
در سیستم مختصات ( xOy) بیایید یک نمودار از تابع بسازیم
و چندین خط از یک مداد از خطوط موازی داده شده توسط معادله. (شکل 4).
پاسخ: 1. اگر، پس هیچ ریشه ای وجود ندارد.
2. اگر، پس یک ریشه.
3. اگر، پس دو ریشه وجود دارد.
IV.3. نابرابری های درجه دوم با پارامتر
№5.
نابرابری را حل کنید 
.
1 راه.
بیایید آن را در نظر بگیریم. سپس - راه حل این نابرابری برای هر ب(شکل 5).
اگر ، پس ما به سمت نابرابری می رویم که مجموعه راه حل های آن در سیستم مختصات نشان داده می شود ( جعبه). (شکل 6).
بیایید انجیر را با هم ترکیب کنیم. 5 و 6.
و اکنون مطابق شکل. 7، برش آن با خطوط مستقیم عمودی، دریافت پاسخ آسان است.
پاسخ: 1. اگر، پس 
.
2. اگر، پس.
3. اگر، پس
روش 2.
اجازه دهید نابرابری را به صورت گرافیکی در سیستم مختصات حل کنیم ( xOb):
. (شکل 8).
بیایید دو مورد را در نظر بگیریم.
1) . سپس نابرابری به شکلی در می آید که .
2) سپس .
نمودار تابع و قسمتی از صفحه حاوی نقاطی که مختصات آن نابرابری را برآورده می کند در شکل 8 نشان داده شده است.
1. اگر، پس .
2. اگر، پس. 3. اگر، پس.
3 راه.
اجازه دهید اکنون یک راه حل گرافیکی در سیستم مختصات ( xOy). برای انجام این کار، اجازه دهید ماژول را گسترش دهیم:
تابع را در نظر بگیرید 
.
ریشه های یک مثلث درجه دوم 
.
بیایید مقایسه کنیم و .
1) از کجا.
کلیت را می گیریم. (شکل 9)
2) از کجا. (شکل 10).
سپس یعنی .
3) از کجا. (شکل 11).
سپس یعنی .
پاسخ: 1. اگر، پس .
2. اگر، پس.
3. اگر، پس.
№6.
تمام مقادیر پارامتر را پیدا کنید الف، که برای آن کوچکترین مقدار تابع است 
بیش از 2.
کافی است تمام مقادیر پارامتر را پیدا کنید الف، برای هر یک از آنها نابرابری برای هر یک صادق است 
. اجازه دهید نابرابری را در فرم بازنویسی کنیم 
., ;
موسسه آموزشی بودجه دولتی
آموزش عمومی متوسطه منطقه سامارا
مدرسه شماره 2 به نام. راه آهن V. Maskina هنر کلیاولینو
منطقه شهرداری کلیاولینسکی
منطقه سامارا
«معادلات
و
نابرابری ها
با پارامترها"
راهنمای آموزشی
کلیاولینو
آموزش
"معادلات و نامساوی با پارامترها"برای دانش آموزان کلاس 10-11
این راهنما ضمیمه برنامه درس انتخابی "معادلات و نابرابری ها با پارامترها" است که آزمون خارجی را گذرانده است (شورای تخصصی علمی و روش شناختی وزارت آموزش و پرورش و علوم منطقه سامارا مورخ 19 دسامبر 2008 توصیه شده است استفاده در موسسات آموزشی منطقه سامارا)
نویسندگان
رومادانوا ایرینا ولادیمیروا
معلم ریاضیات در موسسه آموزشی متوسطه Klyavlinskaya
مدرسه شماره 2 به نام. V. Maskina، منطقه Klyavlinsky، منطقه سامارا
سرباوا ایرینا آلکسیونا
مقدمه…………………………………………………… 3-4
معادلات خطی و نامساوی با پارامترهای……………..4-7
معادلات درجه دوم و نامساوی با پارامترهای……………7-9
معادلات کسری – گویا با پارامترهای………………..10-11
معادلات و نابرابری های غیر منطقی با پارامترهای ……11-13
معادلات مثلثاتی و نامساوی با پارامترها.14-15
معادلات نمایی و نامساوی با پارامترهای ………16-17
معادلات لگاریتمی و نامساوی با پارامتر......16-18
اهداف آزمون یکپارچه دولتی……………………………………………………………………………………………………………………………………………………………
وظایف برای کار مستقل………………………………………………………………………………
مقدمه.
معادلات و نامساوی با پارامترها.
اگر در یک معادله یا نابرابری به برخی از ضرایب مقادیر عددی خاصی داده نشود، بلکه با حروف مشخص شوند، آنها نامیده می‌شوند. پارامترها،و خود معادله یا نابرابری پارامتریک
برای حل یک معادله یا نابرابری با پارامترها باید:
انتخاب کنید معنی خاص- این مقدار پارامتری است که در آن یا هنگام عبور از آن حل معادله یا نابرابری تغییر می کند.
تعریف کنید مقادیر معتبر- اینها مقادیر پارامتری هستند که در آن معادله یا نابرابری معنا پیدا می کند.
حل یک معادله یا نابرابری با پارامترها به این معنی است:
1) تعیین کنید که راه حل ها در چه مقادیر پارامتری وجود دارد.
2) برای هر سیستم مجاز مقادیر پارامتر، مجموعه راه حل های مربوطه را پیدا کنید.
شما می توانید یک معادله را با یک پارامتر با استفاده از روش های زیر حل کنید: تحلیلی یا گرافیکی.
روش تحلیلی شامل کار مطالعه یک معادله با در نظر گرفتن چندین مورد است که هیچ یک از آنها را نمی توان نادیده گرفت.
حل معادلات و نابرابری ها با پارامترهای هر نوع با استفاده از روش تحلیلی مستلزم تجزیه و تحلیل دقیق موقعیت و تحقیق مداوم است که در طی آن نیاز ایجاد می شود. "رفتار دقیق"با پارامتر
روش گرافیکی شامل ساختن نموداری از معادله است که از آن می توان تعیین کرد که چگونه تغییر در پارامتر به ترتیب بر حل معادله تأثیر می گذارد. نمودار گاهی اوقات به شما اجازه می دهد تا به صورت تحلیلی شرایط لازم و کافی برای حل مسئله را فرموله کنید. روش حل گرافیکی به ویژه زمانی مؤثر است که باید تعیین کنید یک معادله بسته به یک پارامتر چند ریشه دارد و این مزیت بدون شک دیدن واضح آن را دارد.
§ 1. معادلات و نابرابری های خطی.
معادله خطی الف x = ب , نوشته شده به شکل کلی، می تواند به عنوان یک معادله با پارامترها در نظر گرفته شود، که در آن x - ناشناخته , الف , ب - پارامترها برای این معادله، مقدار ویژه یا کنترلی پارامتر، مقداری است که در آن ضریب مجهول صفر می شود.
هنگام حل یک معادله خطی با یک پارامتر، مواردی در نظر گرفته می شود که پارامتر برابر با مقدار خاص خود و متفاوت از آن باشد.
مقدار پارامتر ویژه الف ارزش است الف = 0.
ب = 0 یک مقدار پارامتر خاص است ب .
در ب ¹ 0 معادله هیچ راه حلی ندارد
در ب = 0 معادله به شکل زیر خواهد بود: 0x = 0. راه حل این معادله هر عدد واقعی است.
نابرابری های شکل آه > ب و تبر < ب (a ≠ 0)نامساوی خطی نامیده می شوند. مجموعه ای از راه حل های نابرابری آه >ب- فاصله
(; +
),
اگر الف
> 0
، و (-;)
، اگر الف< 0
. به طور مشابه برای نابرابری
اوه<
ب
مجموعه ای از راه حل ها - فاصله(-;),
اگر الف
> 0,
و (; +),
اگر الف< 0.
مثال 1. معادله را حل کنید تبر = 5
راه حل: این یک معادله خطی است.
اگر a = 0، سپس معادله 0 × x = 5هیچ راه حلی ندارد
اگر الف¹ 0، x =- حل معادله
پاسخ دهید: در الف¹ 0، x=
برای a = 0 هیچ راه حلی وجود ندارد.
مثال 2. معادله را حل کنید تبر - 6 = 2a - 3x.
راه حل:این یک معادله خطی است، تبر - 6 = 2a - 3x (1)
تبر + 3x = 2a +6
بازنویسی معادله به صورت (a+3)x = 2(a+3)، دو مورد را در نظر بگیرید:
a= -3و الف¹ -3.
اگر a= -3، سپس هر عدد واقعی Xریشه معادله (1) است. اگر الف¹ -3 ، معادله (1) یک ریشه دارد x = 2.
پاسخ:در a = -3، x 
آر
;
در الف
¹
-3، x = 2.
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞); در چه مقادیر پارامتری الفدر میان ریشه های معادله
2h – 4kh – a 2 + 4a – 4 = 0ریشه های بیشتری وجود دارد 1 ?
راه حل: بیایید معادله را حل کنیم 2h – 4kh – a 2 + 4a – 4 = 0- معادله خطی
2(a - 2) x = a 2 – 4a +4
2(a - 2) x = (a – 2) 2
در a = 2حل معادله 0x = 0هر عددی خواهد بود، از جمله یک بزرگتر از 1.
در الف¹
2 x = 
.
با شرط x > 1، یعنی >1 و >4.
پاسخ:در الف (2) U (4;∞).
مثال 4 . برای هر مقدار پارامتر الفتعداد ریشه های معادله را بیابید ah=8.
راه حل. تبر = 8- معادله خطی
y = الف- خانواده خطوط افقی؛
y = - نمودار یک هذلولی است. بیایید نمودارهایی از این توابع بسازیم.
پاسخ: اگر a = 0، پس معادله هیچ راه حلی ندارد. اگر a ≠ 0، سپس معادله یک راه حل دارد.
مثال 5 . با استفاده از نمودارها، دریابید که معادله چند ریشه دارد:
|x| = آه - 1.
y =| x | ،
y = آه - 1- نمودار خط مستقیمی است که از یک نقطه می گذرد (0;-1).
بیایید نمودارهایی از این توابع بسازیم.
پاسخ: چه زمانی |a|>1- یک ریشه
در | الف|≤1 - معادله ریشه ندارد.
مثال 6 . حل نابرابری تبر + 4 > 2x + a 2
راه حل
:
تبر + 4 > 2x + a
2
(a – 2) x >الف
2
– 4. سه مورد را در نظر می گیریم.
پاسخ دهید. x > a + 2در a > 2; X<а + 2, در الف< 2; در a=2هیچ راه حلی وجود ندارد
§ 2. معادلات درجه دوم و نابرابری ها
معادله درجه دوممعادله ای از فرم است اوه ² + ب x + c = 0 , کجا a≠ 0،
الف، ب ، با - پارامترها
برای حل معادلات درجه دوم با یک پارامتر، می توانید از روش های حل استاندارد با استفاده از فرمول های زیر استفاده کنید:
1
)
ممیز یک معادله درجه دوم:
D
=
ب
² - 4
ac
,
(
²-
ac)
2)
فرمول های ریشه های یک معادله درجه دوم:X
1
=
، X
2
=
,
(X
1,2 =
)
نابرابری درجه دوم نامیده می شود
الف X 2 + ب x + c > 0،الف X 2 + ب x + c< 0, (1), (2)
الف X 2 + ب x + c ≥ 0،الف X 2 + ب x + c ≤ 0،(3), (4)
مجموعه راه حل های نابرابری (3) از ترکیب مجموعه راه حل های نابرابری (1) و معادله به دست می آید. , الف X 2 + ب x + c = 0.مجموعه راه حل های نابرابری (4) را می توان به طور مشابه یافت.
اگر ممیز یک مثلث درجه دوم
الف
X
2
+
ب
x + c
کمتر از صفر است، پس برای a > 0، مثلث برای همه x مثبت است آر.
اگر یک مثلث درجه دوم ریشه داشته باشد (x 1
< х
2
، سپس برای یک > 0 در مجموعه مثبت است(-;
x 2 )
(X 2;
+)
و منفی در بازه
(x 1; x 2 ). اگر الف< 0, то трехчлен положителен на интервале (х
1 ; x 2 ) و برای همه x منفی است (-;
x 1 )(X 2;
+).
مثال 1. معادله را حل کنید ax² - 2 (a – 1)x – 4 = 0.
این یک معادله درجه دوم است
راه حل: اهمیت ویژه a = 0.
در a = 0یک معادله خطی بدست می آوریم 2x - 4 = 0. یک ریشه دارد x = 2.
در a ≠ 0.بیایید متمایز کننده را پیدا کنیم.
D = (a-1)² + 4a = (a+1)²
اگر a = -1،که D = 0 - یک ریشه
بیایید ریشه را با جایگزینی پیدا کنیم a = -1.
-x² + 4x - 4 = 0،یعنی x² -4x + 4 = 0،ما آن را پیدا می کنیم x=2.
اگر a ≠ - 1، آن D
>0
. با استفاده از فرمول ریشه دریافت می کنیم:x= 
;
X 1 = 2، x 2 = -.
پاسخ:در a=0 و a= -1معادله یک ریشه دارد x = 2;در a ≠ 0 و
الف ≠ - 1 معادله دو ریشه داردX 1 = 2، x 2 =-.
مثال 2. تعداد ریشه های این معادله را بیابید x²-2x-8-a=0بسته به مقادیر پارامتر الف
راه حل. اجازه دهید این معادله را به شکل بازنویسی کنیم x²-2x-8=a
y = x²-2x-8- نمودار سهمی است.
y =a- خانواده ای از خطوط افقی.
بیایید نمودارهایی از توابع بسازیم.
پاسخ: چه زمانی الف<-9 ، معادله هیچ راه حلی ندارد. وقتی a=-9، معادله یک راه حل دارد. در a>-9، معادله دو راه حل دارد.
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞); در چه الفنابرابری (a - 3) x 2 – 2ax + 3a – 6 >0برای تمام مقادیر x وجود دارد؟
راه حل.یک مثلث درجه دوم برای همه مقادیر x if مثبت است
a-3 > 0 و D<0, т.е. при а, удовлетворяющих системе неравенств
,
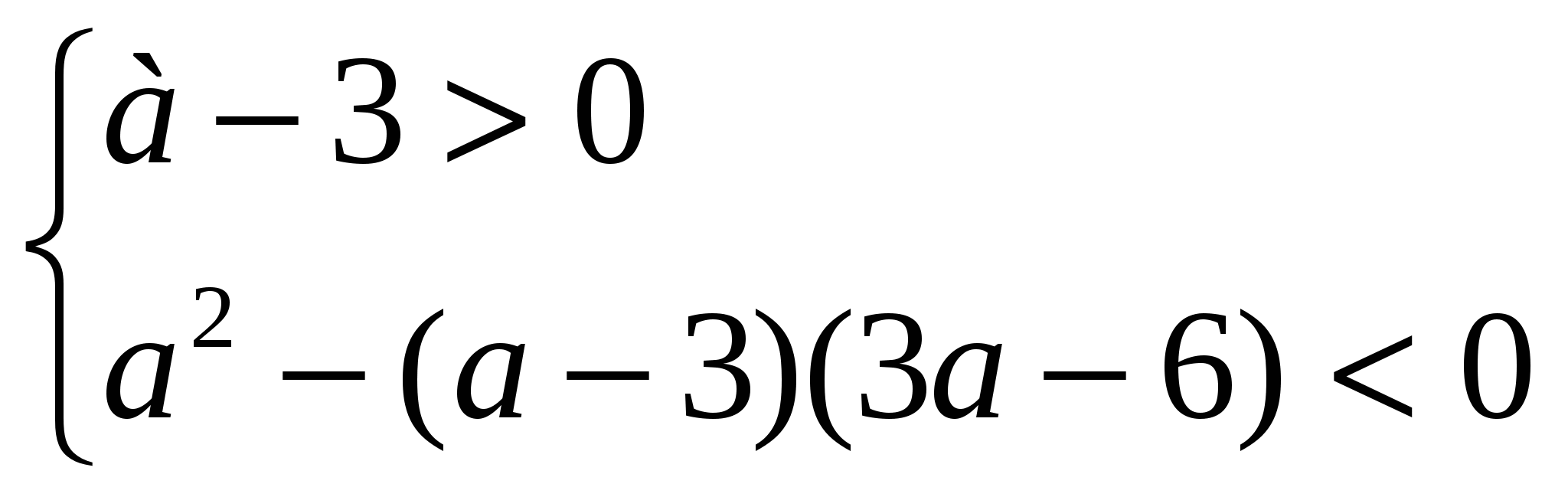
از آنجا نتیجه می گیرد کهالف
> 6
.
پاسخ دهید.الف > 6
§ 3. معادلات گویا کسری با پارامتر،
قابل تقلیل به خطی
فرآیند حل معادلات کسری طبق طرح معمول انجام می شود: کسری با یک عدد صحیح با ضرب هر دو طرف معادله در مخرج مشترک طرف چپ و راست آن جایگزین می شود. پس از آن کل معادله حل می شود، به استثنای ریشه های خارجی، یعنی اعدادی که مخرج را به صفر تبدیل می کنند.
در مورد معادلات با پارامتر، این مشکل پیچیده تر است. در اینجا، برای "حذف" ریشه های اضافی، لازم است مقدار پارامتری را که مخرج مشترک را صفر می کند، پیدا کنیم، یعنی معادلات مربوطه را برای پارامتر حل کنیم.
مثال 1.
معادله را حل کنید 
= 0
راه حل: D.Z: x +2 ≠ 0، x ≠ -2
x – a = 0، x = a.
پاسخ:در a ≠ - 2، x=a
در a = -2هیچ ریشه ای وجود ندارد
مثال 2
.
معادله را حل کنید 
- 
= 
(1)
این یک معادله منطقی کسری است
راه حل:معنی a = 0خاص است در a = 0معادله معنی ندارد و بنابراین ریشه ندارد. اگر a ≠ 0،سپس پس از تبدیل معادله به شکل زیر در می آید: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- معادله درجه دوم
بیایید متمایز کننده را پیدا کنیم 
= (1 – a)² - (a² - 2a - 3) = 4،
ریشه های معادله را پیدا کنیدX
1
= a + 1، x
2
= a - 3.
هنگام انتقال از معادله (1) به معادله (2)، دامنه تعریف معادله (1) گسترش می یابد که می تواند منجر به ظهور ریشه های خارجی شود. بنابراین، تأیید لازم است.
معاینه.بیایید از مقادیر یافت شده حذف کنیم Xآنهایی که در آنها
x 1 +1=0، x 1 +2=0، x 2 +1=0، x 2 +2=0.
اگر X 1 +1=0, یعنی (a+1) + 1=0، آن a= -2.بنابراین،
در a= -2 , X 1 -
اگر X 1 +2=0, یعنی (a+1)+2=0،که a = - 3. بنابراین، زمانی که a = - 3، x 1 - ریشه خارجی معادله (1).
اگر X 2 +1=0, یعنی (a – 3) + 1= 0، آن a = 2. بنابراین، زمانی که a = 2 x 2 - ریشه خارجی معادله (1).
اگر X 2 +2=0, یعنی ( a – 3) + 2 = 0،که a=1. بنابراین، زمانی که a = 1،
X 2 - ریشه خارجی معادله (1).
مطابق با این، زمانی که a = - 3دریافت می کنیم x = - 3 – 3 = -6;
در a = - 2 x = -2 – 3= - 5;
در a = 1 x = 1 + 1 = 2;
در a = 2 x = 2 + 1 = 3.
می توانید پاسخ را یادداشت کنید.
پاسخ: 1) اگر a= -3،که x= -6; 2) اگر a= -2، آن x= -5; 3) اگر a = 0، پس هیچ ریشه ای وجود ندارد. 4) اگر a = 1، آن x=2; 5) اگر a=2، آن x=3; 6) اگر a ≠ -3، a ≠ -2، a ≠ 0، a≠ 1، a ≠ 2، سپس x 1 = a + 1، x 2 = a-3.
§4. معادلات و نابرابری های غیر منطقی
معادلات و نابرابری هایی که در آنها متغیر در زیر علامت ریشه قرار می گیرد نامیده می شود غیر منطقی
حل معادلات غیرمنطقی به انتقال از یک معادله غیرمنطقی به یک معادله منطقی با بالا بردن دو طرف معادله به توان یا جایگزینی یک متغیر خلاصه می شود. هنگامی که هر دو طرف معادله به توان یکنواخت افزایش می یابد، ممکن است ریشه های خارجی ظاهر شوند. بنابراین، هنگام استفاده از این روش، باید با در نظر گرفتن تغییرات در مقادیر پارامتر، تمام ریشه های یافت شده را با جایگزین کردن آنها در معادله اصلی بررسی کنید.
معادله فرم 
=g (x) معادل سیستم است 
نابرابری f (x) ≥ 0 از معادله f (x) = g 2 (x) به دست می آید.
هنگام حل نابرابری های غیرمنطقی، از تبدیل های معادل زیر استفاده می کنیم:
≤ g(x) 
≥g(x) 
مثال 1.
معادله را حل کنید 
= x + 1 (3)
این یک معادله غیرمنطقی است
راه حل:
با تعریف یک ریشه حسابی، معادله (3) معادل سیستم است 
.
در a = 2اولین معادله سیستم دارای شکل است 0 x = 5یعنی هیچ راه حلی ندارد.
در a≠ 2 x= 
.
بیایید دریابیم در چه مقادیریالف
ارزش پیدا کردX
نابرابری را ارضا می کندx ≥ -1: ≥ - 1, 
≥ 0,
کجا a ≤یا a > 2.
پاسخ:در a≤، a > 2 x= ,
در < а ≤ 2
معادله هیچ راه حلی ندارد
مثال 2.
معادله را حل کنید 
= a
(پیوست 4)
راه حل. y
=
y = a- خانواده ای از خطوط افقی.
بیایید نمودارهایی از توابع بسازیم.
پاسخ دهید: در الف<0 - هیچ راه حلی وجود ندارد؛
در الف≥ 0 - یک راه حل
مثال 3
. بیایید نابرابری را حل کنیم(a+1) 
<1.
راه حل. O.D.Z. x ≤ 2. اگر a+1 ≤0، سپس نابرابری برای همه مقادیر مجاز برقرار است X. اگر a+1>0، آن
(a+1) <1.<
کجا X (2- 
2
پاسخ دهید.
X (- ;2در یک (-;-1,
X (2- 2
در الف
(-1;+).
§ 5. معادلات و نابرابری های مثلثاتی.
در اینجا فرمول هایی برای حل ساده ترین معادلات مثلثاتی آورده شده است:
سینکس = a x= (-1) n arcsin a+πn, n ز، 
≤1, (1)
Cos x = a x = ±arccos a + 2 πn, n ز، ≤1.
(2)
اگر
>1، سپس معادلات (1) و (2) هیچ جوابی ندارند.
tan x = a x= آرکتان a + πn, n ز، الف آر
ctg x = a x = arcctg a + πn, n ز، الف آر
برای هر نابرابری استاندارد مجموعه ای از راه حل ها را نشان می دهیم:
1.
گناه x > a arcsin a + 2 πn
ز،
در الف
<-1,
x آر
;
در الف
≥ 1,
هیچ راه حلی وجود ندارد
2. . گناه x< a π - arcsin a + 2 πnZ،
برای a≤-1، هیچ راه حلی وجود ندارد. برای یک > 1،x آر
3.
cos
x
>
الف
-
آرکوس
الف
+ 2
πn
<
x
<
آرکوس
الف
+ 2
πn
,
n
ز
,
در الف<-1,
x آر
; در الف
≥ 1
، هیچ راه حلی وجود ندارد.
4. cos x arccos a+ 2 πnZ،
در a≤-1
، بدون راه حل؛ درالف
> 1,
x
آر
5. tan x > a، arctan a + πnZ
6.tg x< a, -π/2 + πn Z
مثال 1. پیدا کنید الف، که این معادله یک راه حل برای آن دارد:
Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.
راه حل.بیایید معادله را به شکل بنویسیم
باسیستم عامل 2 x + (2 الف -4) cosx +(الف – 5) (a+1) =0،با حل آن به عنوان یک درجه دوم، دریافت می کنیم cosx = 5-الفو cosx = -a-1.
معادله cosx
= 5-
الف
راه حل های ارائه شده دارد -1≤ 5-الف
≤1
4≤
الف≤ 6 و معادله cosx
= -
a-1
ارائه -1≤ -1-الف
≤ 1
-2 ≤
الف
≤0.
پاسخ دهید.
الف
-2; 0 4; 6
مثال 2.
در چه ببه گونه ای وجود دارد که نابرابری وجود دارد 
+
ب> 0 برای همه x ≠ برقرار استπn
,
n
ز
.
راه حل.بگذاریم الف= 0. نابرابری برای b>0 برقرار است. اکنون اجازه دهید نشان دهیم که هیچ b ≤0 شرایط مسئله را برآورده نمی کند. در واقع، کافی است x = را قرار دهیم π /2, اگر الف <0, и х = - π /2 در الف ≥0.
پاسخ دهید.b>0
§ 6. معادلات و نابرابری های نمایی
1. معادله ساعت(x)
f ( x )
=
ساعت(x)
g ( x) در ساعت(x) > 0 معادل مجموعه ای از دو سیستم است 
و 
2. در حالت خاص (h (x)= الف ) معادله الف f(x) = الف g(x) در الف> 0، معادل مجموعه ای از دو سیستم است
و 
3. معادله الف f(x) = ب , کجا الف > 0, الف ≠1, ب> 0، معادل معادله
f (x)= log a b. اتفاق می افتد الف=1 به طور جداگانه در نظر گرفته می شود.
راه حل ساده ترین نابرابری های نمایی بر اساس ویژگی توان است. نابرابری شکلf(الف
x ) > 0 با استفاده از تغییر متغیرتی=
الف
x به حل سیستم نابرابری ها کاهش می یابد 
و سپس به حل نابرابری های نمایی ساده مربوطه.
هنگام حل یک نابرابری غیر دقیق، لازم است ریشه های معادله مربوطه را به مجموعه راه حل های نابرابری شدید اضافه کنید. همانطور که در حل معادلات در تمام مثال های حاوی عبارت الف f (x)، فرض می کنیم الف> 0. مورد الف= 1 به طور جداگانه در نظر گرفته می شود.
مثال 1
.
در چه الفمعادله 8 x = 
فقط ریشه های مثبت دارد؟
راه حل.
با خاصیت تابع نمایی با پایه بزرگتر از یک، x>0 داریم 8
X >1 >1
> 0، از کجاالف
(1,5;4).
پاسخ دهید.
الف
(1,5;4).
مثال 2. حل نابرابری الف 2 ∙2 x > الف
راه حل. بیایید سه مورد را در نظر بگیریم:
1.
الف< 0
. از آنجایی که سمت چپ نابرابری مثبت و سمت راست منفی است، نابرابری برای هر x برقرار است. آر.
2. الف=0.
3.
الف
> 0
.
الف
2
∙2
x
هیچ راه حلی وجود ندارد.
2
x
>
> الف 2
x > - ورود به سیستم
پاسخ دهید.
الف آردر الف
X
الف
> 0; هیچ راه حلی برای (-
=0; X 2
x > - ورود به سیستم; +ورود به سیستم) در
.
a> 0
§ 7. معادلات لگاریتمی و نامساوی اجازه دهید چند معادل مورد استفاده در حل را ارائه کنیم
معادلات لگاریتمی و نابرابری ها
1. معادله log f (x) g (x) = log f (x) h (x) معادل سیستم است الف >0, الفبه ویژه، اگر
=0; X الف
≠1، سپس الف
g(x)= log 
2.
معادله h (x) الف
ورود به سیستم g(x)=bالف
ب (
الف
>0,
g(x)=
یک ≠
1، g(x) > 0). =0; X f ( x )
g (x) ≤
=0; X f ( x )
ساعت(x3. نابرابری 
و 
) معادل ترکیبی از دو سیستم است: اگر یک،
=0; X الف
b اعداد هستند، a >0، a ≠1، پس 
=0; X الف
f(x) ≤ b 
مثال 1.
f(x)>b 
راه حلمعادله را حل کنید الف 4 , الف > 0, الف. بیایید ODZ را پیدا کنیم: x > 0، x ≠
≠ 1. معادله را تبدیل کنید 
ورود به سیستم =0; X الف
x ≠ 1. معادله را تبدیل کنید x – 2 = 4 – =0; X الف
x x + =0; X الف
x = - 3
– 6 = 0، از این رو الف x = =0; X الف
x = 2
-3 و الف x = الف
4
الف
– 3
=
الف 2. شرط x = الف
2
=
الف
4
4 یا
پاسخ:روی ODZ انجام نمی شود. الف x = الف-3، x = الف
(0; 1) 
(1; ).
مثال 2 . 2 در الفبزرگترین ارزش را پیدا کنید
2
≠ 1. معادله را تبدیل کنید 
-
+
الف
، که برای آن معادله
راه حل.
= 0 راه حل دارد. =
تیما جایگزین خواهیم ساختتی 2
–
تی +
الف
و معادله درجه دوم 2 را بدست می آوریم= 0. حل، پیدا می کنیم = 1-8
الف
D = 0. حل، پیدا می کنیم≥0, 1-8
الف
≥0 
الف
≤.
در الف . در نظر بگیریمتی= >0.
پاسخ دهید. الف =
مثال 3 . = معادله درجه دوم ریشه دارد=0; X(x 2 – 2 x + الف ) > - 3
راه حل.
حل نابرابری 
بیایید سیستم نابرابری ها را حل کنیم 1,2
ریشه های سه جمله ای مربع x 
= 1 ± 3,4
آنها 
.
مقادیر پارامتر بحرانی: الف= 1 و الف= 9.
اجازه دهید X 1 و X 2 مجموعه‌ای از راه‌حل‌های نابرابری اول و دوم باشند
X 1 
X 2
= X - راه حل برای نابرابری اصلی.
در 0<
الف
<1 Х
1
= (-
;1 - )(1 + ; +)، درالف> 1 x 1 = (-;+).
برای ≤ -1 x € (-∞؛ 1/(a – 1)].<
الف
< 9 Х
2
= (1 -; 1 +)، درالف≥9 X 2 - بدون راه حل.
بیایید سه مورد را در نظر بگیریم:
1. 0<
الف
≤1 X = (1 - ;1 - )(1 + ;1 +).
2. 1 <
الف
< 9 Х = (1 -;1 +).
3. الف≥ 9 X - بدون راه حل.
اهداف آزمون دولتی یکپارچه
سطح بالا C1, C2
مثال 1. همه مقادیر را پیدا کنید r، که برای آن معادله
r ∙ ctg 2x+2sinx+ ص= 3 حداقل یک ریشه دارد.
راه حل.بیایید معادله را تبدیل کنیم
r ∙ (
- 1) + 2sinx + ص= 3، sinx = t، تی 
، تی 
0.
-
ص+2t+ ص
= 3,
+ 2 t = 3، 3 -2t = ، 3t 2 – 2t 3 = ص
.
اجازه دهید f(y) = 3
تی 2
– 2
تی 3
. بیایید مجموعه مقادیر تابع را پیدا کنیمf(x) در 
. در /
= 6
تی – 6
تی 2
, 6
تی - 6
تی 2
= 0,
تی 1
=0,
تی 2
= 1.
f(-1) = 5,
f(1) = 1.
در تی ,
E(f) =
,
در تی ,
E(f) =
، یعنی چه زمانی تی ,
E(f) =
.
به معادله 3تی 2
– 2
تی 3
=
ص
(از این رو داده شده) حداقل یک ریشه لازم و کافی داشتص
E(f) یعنی ص
.
پاسخ دهید.
.
مثال 2.
در چه مقادیر پارامتریالفمعادله ≠ 1. معادله را تبدیل کنید 
(4
x 2
– 4
الف
+
الف
2
+7) = 2 دقیقاً یک ریشه دارد؟
راه حل.بیایید معادله را به یک معادل با این تبدیل کنیم:
4x 2 - 4 الف + الف 2 + 7 = (x 2 + 2) 2.
توجه داشته باشید که اگر یک عدد x ریشه معادله حاصل باشد، عدد – x نیز ریشه این معادله است. طبق شرط، این امکان پذیر نیست، بنابراین تنها ریشه عدد 0 است.
پیدا خواهیم کرد الف.
4∙ 0 2 - 4الف + الف 2 +7 = (0 2 + 2) 2 ,
الف 2 - 4الف +7 = 4, الف 2 - 4الف +3 = 0, الف 1 = 1, الف 2 = 3.
معاینه.
1)
الف
1
= 1. سپس معادله به نظر می رسد:≠ 1. معادله را تبدیل کنید (4
x 2
+4) = 2. حلش کنیم
4x 2 + 4 = (x 2 + 2) 2، 4x 2 + 4 = x 4 + 4 x 2 + 4، x 4 = 0، x = 0 تنها ریشه است.
2)
الف
2
= 3. معادله به نظر می رسد:≠ 1. معادله را تبدیل کنید (4
x 2
+4) =2 x = 0 تنها ریشه است.
پاسخ دهید. 1; 3
سطح بالا C4، C5
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞); همه مقادیر را پیدا کنید pکه برای آن معادله
x 2 - ( r+ 3)x + 1= 0 دارای ریشه های صحیح است و این ریشه ها راه حل های نابرابری هستند: x 3 – 7 r x 2 + 2x 2 - 14 r x - 3x +21 r ≤ 0.
راه حل.
اجازه دهید x 1,
X 2
– ریشه های عدد صحیح معادله x 2
– (r
+ 3)x + 1= 0. سپس طبق فرمول ویتا برابری های x 1
+ x 2
=
r
+ 3، x 1
∙ x 2
= 1. حاصل ضرب دو عدد صحیح x 1
، X 2
فقط در دو مورد می تواند برابر با یک باشد: x 1
= x 2
= 1 یا x 1
= x 2
= - 1. اگر x 1
= x 2
= 1، پسr
+ 3 = 1+1 = 2r
= - 1; اگر x 1
= x 2
= - 1، سپسr
+ 3 = - 1 – 1 = - 2 r
= - 5. بیایید بررسی کنیم که آیا ریشه های معادله x هستند 2
– (r
+ 3) x + 1 = 0 در موارد توصیف شده توسط راه حل های این نابرابری. به مناسبتr
= - 1، x 1
= x 2
= 1 ما داریم
1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – درست است. برای این مناسبت r= - 5، x 1 = x 2 = - 1 ما داریم (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 - درست است. بنابراین، شرایط مشکل فقط برآورده می شود r= - 1 و r = - 5.
پاسخ دهید.r 1 = - 1 و r 2 = - 5.
مثال 4. تمام مقادیر مثبت پارامتر را پیدا کنید الف، که عدد 1 متعلق به دامنه تعریف تابع است
در
= (الف 
-
الف 
).
پیش نمایش:
وزارت آموزش و پرورش منطقه مسکو
موسسه آموزشی دولتی NPO مدرسه حرفه ای شماره 37
پروژه:
معادلات ربع و نابرابری با پارامترها"
تکمیل شد -
ماتسوک گالینا نیکولاونا،
معلم ریاضیات، موسسه آموزشی دولتی NPO
مدرسه حرفه ای شماره 37 MO.
G.Noginsk، 2011
1. مقدمه
4. روش حل معادلات درجه دوم در شرایط اولیه.
6. روش حل نابرابری های درجه دوم با پارامترها به صورت کلی.
7. روش حل نابرابری های درجه دوم در شرایط اولیه.
8. نتیجه گیری.
9. ادبیات.
- مقدمه.
وظیفه اصلی آموزش ریاضیات در یک مدرسه فنی حرفه ای تضمین تسلط قوی و آگاهانه دانش آموزان بر سیستم دانش و مهارت های ریاضی ضروری در زندگی و کار روزمره است که برای مطالعه رشته های مرتبط و ادامه تحصیل و همچنین در فعالیت های حرفه ای کافی است. نیاز به فرهنگ ریاضی به اندازه کافی بالا دارد.
آموزش ریاضی پروفایل از طریق حل مسائل کاربردی مربوط به حرفه فلزکاری، کار تاسیسات برقی و نجاری انجام می شود. برای زندگی در جامعه مدرن، توسعه یک سبک ارتباطی ریاضی مهم است که خود را در مهارت های ذهنی خاصی نشان می دهد. مشکلات مربوط به پارامترها دارای ارزش تشخیصی و پیش آگهی هستند. با کمک آنها می توانید دانش خود را از بخش های اصلی ریاضیات ابتدایی، سطح تفکر منطقی و مهارت های تحقیق اولیه آزمایش کنید.
آموزش وظایف با پارامترها مستلزم آن است که دانش آموزان تلاش ذهنی و ارادی فراوان، توجه توسعه یافته و پرورش ویژگی هایی مانند فعالیت، ابتکار خلاق و کار شناختی جمعی داشته باشند. مشکلات مربوط به پارامترها برای مطالعه در طول تکرار عمومی در سال 2 به منظور آمادگی برای گواهینامه نهایی دولتی و در سال 3 در کلاس های اضافی برای آماده سازی دانش آموزانی که تمایل به شرکت در امتحانات نهایی در قالب آزمون دولتی یکپارچه را ابراز کرده اند جهت گیری می شود. .
جهت اصلی نوسازی آموزش ریاضیات، توسعه مکانیسم هایی برای صدور گواهینامه نهایی از طریق معرفی آزمون دولتی واحد است. در سال های اخیر مسائل مربوط به پارامترها در تکالیف ریاضی مطرح شده است. چنین وظایفی برای آزمون ورودی دانشگاه الزامی است. ظهور چنین مسائلی بسیار مهم است، زیرا با کمک آنها، تکنیک مهارت در فرمول های ریاضیات ابتدایی، روش های حل معادلات و نابرابری ها، توانایی ایجاد یک زنجیره منطقی استدلال، و سطح تفکر منطقی متقاضی است. مورد آزمایش قرار می گیرند. تجزیه و تحلیل نتایج آزمون یکپارچه قبلی در چندین سال گذشته نشان می دهد که فارغ التحصیلان در حل چنین وظایفی با مشکلات زیادی روبرو هستند و بسیاری حتی آنها را شروع نمی کنند. اکثر آنها یا اصلاً نمی توانند با چنین وظایفی کنار بیایند، یا محاسبات دست و پا گیر ارائه می دهند. دلیل این امر نبود سیستم تکالیف در این زمینه در کتاب های درسی مدارس است. در این راستا، نیاز به اجرای سرفصل های ویژه در گروه های فارغ التحصیل در آمادگی برای امتحانات در زمینه حل مسائل با پارامترها و مسائل با ماهیت کاربردی مرتبط با گرایش حرفه ای بود.
مطالعه این موضوعات برای دانش آموزان سال سوم در نظر گرفته شده است که می خواهند یاد بگیرند که چگونه مسائل با سطح پیچیدگی افزایش یافته در جبر و آغاز تجزیه و تحلیل را حل کنند. حل چنین مشکلاتی برای آنها مشکلات قابل توجهی ایجاد می کند. این به دلیل این واقعیت است که هر معادله یا نابرابری با پارامترها نشان دهنده یک کلاس کامل از معادلات و نابرابری های معمولی است که برای هر یک از آنها باید یک راه حل به دست آورد.
در فرآیند حل مسائل با پارامترها، زرادخانه فنون و روش های تفکر انسان به طور طبیعی شامل استقراء و استنتاج، تعمیم و مشخص کردن، تجزیه و تحلیل، طبقه بندی و نظام مندسازی و قیاس است. از آنجایی که برنامه درسی در مدارس فنی حرفه ای، مشاوره در زمینه ریاضیات را که در برنامه کلاس ها گنجانده شده است، برای دانش آموزانی که آموزش ریاضی کافی دارند، به موضوع مورد مطالعه علاقه نشان می دهند و هدف بعدی ورود به دانشگاه را دارند، در نظر گرفته شده است، توصیه می شود. استفاده از ساعات مشخص شده برای حل مسائل مربوط به پارامترهای آمادگی برای المپیادها، مسابقات ریاضی، انواع مختلف امتحانات، به ویژه آزمون یکپارچه دولتی. حل چنین مشکلاتی به ویژه برای اهداف کاربردی و عملی مرتبط است که به انجام مطالعات مختلف کمک می کند.
2. اهداف، وظایف اصلی، روش ها، فناوری ها، الزامات دانش.
اهداف پروژه:
- شکل گیری توانایی ها و مهارت ها در حل مسائل با پارامترها که به مطالعه معادلات درجه دوم و نابرابری ها خلاصه می شود.
- ایجاد علاقه به موضوع، توسعه توانایی های ریاضی، آماده سازی برای آزمون دولتی واحد.
- گسترش درک ریاضی تکنیک ها و روش های حل معادلات و نابرابری ها.
- توسعه تفکر منطقی و مهارت های تحقیق.
- مشارکت در فعالیت های خلاقانه، پژوهشی و آموزشی.
- فراهم کردن شرایط برای کار خلاقانه مستقل.
- تقویت تلاش های ذهنی و ارادی دانش آموزان، توسعه توجه، فعالیت، ابتکار خلاق و مهارت های کار شناختی جمعی.
اهداف اصلی پروژه:
- فراهم کردن فرصتی برای دانش آموزان برای درک علاقه خود به ریاضیات و فرصت های فردی برای توسعه آن.
- ترویج کسب دانش و مهارت های واقعی.
- نشان دادن اهمیت عملی مسائل با پارامترها در زمینه تحقیقات کاربردی.
- آموزش روش های حل معادلات و نابرابری های استاندارد و غیر استاندارد.
- برای تعمیق دانش در ریاضیات، ایجاد علاقه پایدار به موضوع.
- توانایی های ریاضی دانش آموزان را شناسایی و توسعه دهید.
- برای ورود به دانشگاه آمادگی لازم را فراهم کنید.
- آماده سازی برای فعالیت های حرفه ای که نیاز به فرهنگ ریاضی بالایی دارند.
- سازماندهی فعالیت های پژوهشی و پروژه ای که به توسعه مهارت های فکری و ارتباطی کمک می کند.
روش های مورد استفاده در کلاس ها:
- سخنرانی - برای انتقال مطالب نظری، همراه با گفتگو با دانش آموزان.
- سمینارها - برای ادغام مطالب در مورد بحث در مورد نظریه.
- کارگاه - حل مسائل ریاضی.
- بحث - برای ارائه استدلال برای راه حل های خود.
- اشکال مختلف فعالیت های گروهی و فردی.
- فعالیت های پژوهشی که از طریق: کار با مطالب آموزشی، تهیه پیام، دفاع از چکیده ها و آثار خلاقانه سازماندهی می شود.
- سخنرانی – ارائه با استفاده از کامپیوتر و پروژکتور.
تکنولوژی های مورد استفاده:
- سیستم آموزشی سخنرانی-سمینار.
- فناوری اطلاعات و ارتباطات.
- روش تحقیق در تدریس با هدف پرورش توانایی های تفکر.
- یادگیری مبتنی بر مسئله، که با طرح مسئله، بحث در مورد گزینه‌های مختلف برای مسئله، انگیزه‌ای برای تحقیق فراهم می‌کند.
- فناوری روش فعالیت که به توسعه علایق شناختی دانش آموزان کمک می کند.
الزامات دانش دانش آموزان.
در نتیجه مطالعه روش های مختلف حل معادلات درجه دوم و نابرابری ها با پارامترها، دانش آموزان باید مهارت های زیر را کسب کنند:
- مفهوم پارامتر را در یک معادله درجه دوم و نابرابری درجه دوم کاملا درک کنید.
- قادر به حل معادلات درجه دوم با پارامترها باشد.
- قادر به حل نابرابری های درجه دوم با پارامترها باشد.
- ریشه های تابع درجه دوم را پیدا کنید.
- نمودارهایی از توابع درجه دوم بسازید.
- سه جمله درجه دوم را کاوش کنید.
- به کارگیری روش های عقلانی دگرگونی هویت.
- از متداول ترین تکنیک های اکتشافی استفاده کنید.
- بتوانید دانش کسب شده را هنگام کار بر روی رایانه شخصی به کار ببرید.
اشکال کنترل
- دروس - خود ارزیابی و ارزیابی رفقا.
- ارائه پروژه های آموزشی.
- تست کردن
- رتبه بندی - جدول
- مشکلات تکالیف از مجموعه های آزمون یکپارچه دولتی سال های گذشته.
- تست ها
3. روش حل معادلات درجه دوم با پارامترها به صورت کلی.
از مشکلات مربوط به پارامترها نترسید. اول از همه، هنگام حل معادلات و نابرابری ها با پارامترها، باید کاری را انجام دهید که هنگام حل هر معادله و نابرابری انجام می شود - معادلات یا نابرابری های داده شده را در صورت امکان به شکل ساده تر کاهش دهید: عبارت منطقی را فاکتور کنید، آن را کاهش دهید، قرار دهید فاکتور خارج از براکت و غیره .d. مشکلاتی وجود دارد که می توان آنها را به دو دسته بزرگ تقسیم کرد.
کلاس اول شامل نمونه هایی است که در آنها لازم است معادله یا نابرابری برای تمام مقادیر ممکن یک پارامتر حل شود.
کلاس دوم شامل نمونه هایی است که در آنها لازم است نه همه راه حل های ممکن، بلکه تنها راه حل هایی که برخی شرایط اضافی را برآورده می کنند، پیدا کنید. دسته چنین مشکلاتی پایان ناپذیر است.
قابل فهم ترین راه برای حل چنین مسائلی برای دانش آموزان این است که ابتدا همه راه حل ها را بیابند و سپس راه حل هایی را انتخاب کنند که شرایط اضافی را برآورده کنند.
هنگام حل مسائل با پارامترها، گاهی اوقات ساختن نمودارها در صفحه معمولی (x، y) راحت است، و گاهی اوقات بهتر است نمودارها را در صفحه (x، a) در نظر بگیرید، جایی که x متغیر مستقل و "a" است. پارامتر است. این در درجه اول در مسئله ای امکان پذیر است که در آن شما باید نمودارهای ابتدایی آشنا بسازید: خطوط مستقیم، سهمی ها، دایره ها و غیره. به‌علاوه، طرح‌های نمودارها گاهی کمک می‌کنند تا «پیشرفت» راه‌حل را به وضوح ببینید.
هنگام حل معادلات f (x,a) = 0 و نابرابری های f (x,a) › 0 باید به یاد داشته باشیم که اول از همه راه حل برای مقادیر پارامتری در نظر گرفته می شود که در آن ضریب در بالاترین مقدار است. توان x از مثلث مربع f (x ,a)، در نتیجه درجه را کاهش می دهد. معادله درجه دوم A(a) x 2 + B(a) x + C(a) = 0 در A(a) = 0 اگر B(a) ≠ 0 باشد به خطی تبدیل می شود و روش های حل معادلات درجه دوم و خطی متفاوت است.
اجازه دهید فرمول های اصلی کار با معادلات درجه دوم را به یاد بیاوریم.
معادله فرم ah 2 + در + c = 0، که در آن x R مجهولات هستند، a, b, c عباراتی هستند که فقط به پارامترها بستگی دارند و a ≠ 0 معادله درجه دوم نامیده می شود و D = b 2 – 4ac ممیز یک مثلث درجه دوم نامیده می شود.
اگر D
اگر D > 0 باشد، معادله دو ریشه متفاوت دارد
x 1 = , x 2 = و سپس ax 2 + in + c = a (x – x 1) (x – x 2).
این ریشه ها از طریق ضرایب معادله با فرمول های ویتا مرتبط می شوند
اگر D = 0 باشد، معادله دارای دو ریشه متقابل x است 1 = x 2 = و سپس ax 2 + in + c = a (x – x 1) 2 . در این حالت معادله یک راه حل دارد.
وقتی، یعنی = 2k، ریشه های معادله درجه دوم با فرمول x تعیین می شوند 1,2 = ,
برای حل معادله درجه دوم کاهش یافته x 2 + px + q = 0
فرمول استفاده شده x است 1,2 = - و همچنین فرمول های Vieta
نمونه ها حل معادلات:
مثال 1. + =
راه حل:
برای یک ≠ - 1، x ≠ 2، x را می گیریم 2 + 2ax – 3b + 4 = 0 و ریشه
x 1 = - a -، x 2 = -a + ، موجود در
A 2 + 2a - 4 0، یعنی. در
حالا بیایید بررسی کنیم که آیا چنین چیزی وجود دارد که یا x 1 یا x 2 برابر است با 2. x = 2 را در معادله درجه دوم جایگزین کنید و a = - 8 بدست می آوریم.
ریشه دوم در این مورد برابر است با(طبق قضیه ویتا) و برای a = - 8 برابر است با 14.
پاسخ: برای a = - 8، تنها راه حل x = 14 است.
اگر یک (- ∞؛ - 8) (- 8؛ - 4) (1؛ + ∞) - دو ریشه x 1 و x 2;
اگر a = - تنها راه حل x =به ترتیب؛
اگر a (- 4؛ 1)، آنگاه x .
گاهی اوقات معادلات با عبارت کسری به معادلات درجه دوم کاهش می یابد. معادله زیر را در نظر بگیرید.
مثال 2. - =
راه حل: وقتی a = 0 معنی ندارد، مقدار x باید شرایط را برآورده کند: x -1، x -2. ضرب تمام عبارات معادله در (x + 1) (x +2) 0,
x 2 – 2 (a – 1)x + a 2 می گیریم – 2a – 3 = 0، معادل این. ریشه های آن:
x 1 = a + 1، x 2 = - 3. اجازه دهید ریشه های خارجی را از این ریشه ها انتخاب کنیم، i.e. آنهایی که مساوی – 1 و – 2 هستند:
X 1 = a + 1 = - 1، a = - 2، اما با a = - 2 x 2 = - 5;
X 1 = a + 1 = - 2، a = - 3، اما با a = - 3 x 2 = - 6;
X 2 = a - 3 = - 1، a = 2، اما با a = 2 x 1 = 3;
X 2 = a - 3 = - 2، a = 1، اما با a = 1 x 1 = 2.
پاسخ: برای ≠ 0، a ≠ 2، a ≠ - 3، a ≠ 1 x 1 = a + 1، x 2 = a – 3;
وقتی a = - 2 x = - 5; وقتی a = - 3 x = - 6.
4. روش حل معادلات درجه دوم در شرایط اولیه.
شرایط برای معادلات درجه دوم پارامتری متفاوت است. به عنوان مثال، شما باید مقدار پارامتری را پیدا کنید که ریشه های آن عبارتند از: مثبت، منفی، دارای علائم مختلف، بزرگتر یا کمتر از یک عدد خاص و غیره. برای حل آنها باید از خواص ریشه های تبر معادله درجه دوم استفاده کنید 2 + در + c = 0.
اگر D > 0، a > 0، آنگاه معادله دارای دو ریشه واقعی متفاوت است که علائم آنها برای c > 0 یکسان و مخالف علامت ضریب b و برای c است.
اگر D = 0، a > 0 باشد، معادله دارای ریشه های واقعی و مساوی است که علامت آن مخالف علامت ضریب b است.
اگر D 0 باشد، معادله هیچ ریشه واقعی ندارد.
به طور مشابه، ما می توانیم خواص ریشه های معادله درجه دوم را برای a تعیین کنیم
- اگر در یک معادله درجه دوم ضرایب a و c را مبادله کنیم، معادله ای به دست می آید که ریشه های آن معکوس ریشه های داده شده است.
- اگر در یک معادله درجه دوم علامت ضریب b را تغییر دهیم، معادله ای به دست می آید که ریشه های آن مخالف ریشه های ضریب داده شده است.
- اگر در یک معادله درجه دوم ضرایب a و c دارای نشانه های متفاوتی باشند، ریشه واقعی دارد.
- اگر a > 0 و D = 0، سمت چپ معادله درجه دوم یک مربع کامل است و بالعکس، اگر سمت چپ معادله یک مربع کامل باشد، a> 0 و D = 0 است.
- اگر همه ضرایب معادله گویا باشند و ممیز یک مربع کامل را بیان کند، ریشه های معادله گویا هستند.
- اگر محل ریشه ها را نسبت به صفر در نظر بگیریم، قضیه ویتا را اعمال می کنیم.
انتخاب ریشه های یک مثلث درجه دوم با توجه به شرایط و مکان صفرهای یک تابع درجه دوم روی خط اعداد.
فرض کنید f (x) = ax 2 + in + c، a 0، ریشه x 1 ˂ x 2، ˂ .
محل قرارگیری ریشه ها روی خط اعداد. | شرط لازم و کافی. |
|
x 1، x 2 | و f () > 0، D 0، x 0 |
|
x 1، x 2 > | و f ( ) > 0، D 0، x 0 > |
|
x 1 2 | و f () |
|
1، x 2 . | و f ( ) > 0، D 0، و f ( ) > 0 0 . |
|
1 2 | و f ( ) > 0 و f ( ) |
|
x 1 2 | و f () ) > 0 |
|
x 1 2 | و f () ) |
پاسخ: x € [(a – 1)/3; +∞) برای یک € (-∞; 0)ᴗ(1; +∞); تعیین کنید که معادله در چه مقادیری است
x 2 – 2 (a – 1) x + 2a + 1 = 0
- ریشه ندارد:
شرط لازم و کافی د
D = (a – 1) 2 – 2a – 1 = a 2 – 4a
- ریشه دارد:
D 0، D = (a – 1) 2 – 2a – 1 0، a
- یک ریشه دارد:
- دو ریشه دارد:
D > 0، یعنی یک
- ریشه های مثبت دارد:
2(a – 1) > 0 a 4
اگر سوال این است که "دو ریشه مثبت دارد"، سیستم باید جایگزین شود D > 0;
- ریشه های منفی دارد:
2 (a - 1)
- ریشه نشانه های مختلفی دارد، یعنی. یکی مثبت و دیگری منفی:
الف ;
وضعیت استفاده از آن ضروری نیست، x کافی است 1×2
- یکی از ریشه ها برابر با 0 است:
شرط کافی ضروری این است که عبارت آزاد معادله برابر با صفر باشد، یعنی. 2a + 1 = 0، a = -1/2.
علامت ریشه دوم یا با جایگزین کردن a = -1/2 در معادله اصلی یا به عبارت ساده تر، با قضیه x ویتا تعیین می شود. 1 + x 2 = 2 (a – 1)، و پس از جایگزینی a = -1/2، x را بدست می آوریم 2 = - 3، یعنی برای a = -1/2 دو ریشه: x 1 = 0، x 2 = - 3.
مثال 4 . معادله در چه مقادیری از پارامتر a انجام می شود
(a – 2) x 2 – 4ax +3 -2a = 0 راه حل منحصر به فردی دارد که نابرابری x را برآورده می کند
راه حل.
ممیز 2 – (a – 2)(3 – 2a)
4a 2 – 3a + 6 + 2a 2 – 4a = 6a 2 – 7a + 6
از 49 - 144 = - 95 و ضریب اول 6 استسپس 6a 2 – 7a + 6 برای همه x R.
سپس x 1.2 = .
با توجه به شرایط مسئله x2، سپس نابرابری را دریافت می کنیم
ما داریم:
برای همه یک R صادق است.
6a 2 – 7a + 6 6a 2 – 7a – 10 2
A 1.2 = 1/12 (7 17)، و 1 = 2، و 2 = - 5/6.
بنابراین -5/6
پاسخ: -
5. پارامتر به عنوان یک متغیر مساوی.
در تمام وظایف تحلیل شدهپارامتر به عنوان یک عدد ثابت اما ناشناخته در نظر گرفته شد. در همین حال، از نقطه نظر رسمی، یک پارامتر یک متغیر و «برابر» با سایر موارد موجود در مثال است. به عنوان مثال، با این نمای پارامتر فرم f (x; a)، توابع نه با یک (مانند قبل)، بلکه با دو متغیر تعریف می شوند. چنین تفسیری طبیعتاً نوع دیگری (یا بهتر است بگوییم، روش حلی که این نوع را تعریف می کند) از مسائل مربوط به پارامترها را تشکیل می دهد. اجازه دهید یک راه حل تحلیلی از این نوع را نشان دهیم.
مثال 5. در صفحه xy، تمام نقاطی را که هیچ یک از منحنی های خانواده y = x از آنها عبور نمی کند، نشان دهید. 2 - 4рх + 2р 2 - 3، که در آن p یک پارامتر است.
راه حل: اگر (x 0;y 0 ) نقطه ای است که هیچ یک از منحنی های یک خانواده معین از آن عبور نمی کند، سپس مختصات این نقطه معادله اصلی را برآورده نمی کند. در نتیجه، مسئله به یافتن رابطه ای بین x و y خلاصه شد به طوری که معادله داده شده در شرط هیچ راه حلی نداشته باشد. به راحتی می توان با تمرکز بر متغیرهای x و y، بلکه بر روی پارامتر p، وابستگی مورد نظر را به دست آورد. در این صورت، یک ایده سازنده به وجود می آید: این معادله را نسبت به p درجه دوم در نظر بگیرید. ما داریم
2р 2 - 4рх+ x 2 – y – 3 = 0. ممیز= 8x2 + 8y + 24 باید منفی باشد. از اینجا y ˂ - x می گیریم 2 – 3، بنابراین، مجموعه مورد نیاز تمام نقاط صفحه مختصات است که "زیر" سهمی y = - x است. 2 – 3.
پاسخ: y 2 – 3
6. روش حل نابرابری های درجه دوم با پارامترها
به طور کلی.
نابرابری های درجه دوم (سخت و غیر دقیق) شکل
مقادیر قابل قبول آن دسته از مقادیر پارامتری هستند که a، b، c برای آنها معتبر است. حل نابرابری های درجه دوم به صورت تحلیلی یا گرافیکی راحت است. از آنجایی که نمودار یک تابع درجه دوم یک سهمی است، پس برای a > 0، شاخه های سهمی به سمت بالا هدایت می شوند، برای یک
موقعیت های مختلف سهمی f (x) = تبر 2 + در + s، a 0 برای > 0 در شکل 1 نشان داده شده است
الف) ب) ج)
الف) اگر f (x) > 0 و D R;
ب) اگر f (x) > 0 و D = 0، آنگاه x ;
ج) اگر f (x) > 0 و D > 0، آنگاه x (- ; x 1 ) (x 2 ; + ).
موقعیت سهمی به طور مشابه برای a در نظر گرفته می شود
مثلا یکی از سه موردی که
برای 0 و f (x) > 0 x (x 1; x 2);
برای 0 و f (x) (- ; x 1 ) (x 2 ; + ).
به عنوان مثال، حل یک نابرابری را در نظر بگیرید.
مثال 6. حل نابرابری x 2 + 2x + a > 0.
فرض کنید D ممیز مثلث x باشد 2 + 2x + a > 0. برای D = 0، برای a = 1، نابرابری به شکل زیر است:
(x + 1) 2 > 0
برای هر مقدار واقعی x به جز x = -1 صادق است.
وقتی D > 0 باشد، یعنی. در x، سه جمله ای x 2 + 2x + a دو ریشه دارد: - 1 -و
1 + و راه حل نابرابری بازه است
(- ; - 1 – ) (- 1 + ; + )
این نابرابری به راحتی به صورت گرافیکی قابل حل است. برای انجام این کار، اجازه دهید آن را در فرم نشان دهیم
X 2 + 2x > - a
و یک نمودار از تابع y = x بسازید 2 + 2 برابر
ابسیساهای نقاط تلاقی این نمودار با خط مستقیم y = - a ریشه های معادله x هستند. 2 + 2x = - a.
پاسخ:
برای –a > - 1، یعنی. در یک, x (- ; x 1 ) (x 2 ;+ );
در – a = - 1، یعنی. برای a = 1، x هر عدد واقعی است به جز - 1.
در – a ، یعنی برای یک > 1، x هر عدد واقعی است.
مثال 7 . حل نابرابری cx 2 – 2 (s – 1)x + (s + 2)
وقتی c = 0 شکل می گیرد: 2x + 2راه حل x خواهد بود
اجازه دهید نماد f (x) = cx را معرفی کنیم 2 – 2 (s – 1)x + (s + 2)جایی که c ≠ 0.
در این مورد نابرابری f(x)
فرض کنید D ممیز f(x) باشد. 0.25 D = 1 - 4s.
اگر D > 0 باشد، یعنی اگر با> 0.25، سپس علامت f (x) با علامت c برای هر مقدار واقعی x، یعنی. f(x)> 0 برای هر x R، که به معنای c > است 0.25 نابرابری f(x)
اگر D = 0 باشد، یعنی c = 0.25، سپس f (x) = (0.25 x + 1.5) 2، یعنی f (x) 0 برای هر کدام
X R. بنابراین، برای c = 0.25 نابرابری f (x)
مورد D را در نظر بگیرید 0). f (x) = 0 برای دو مقدار واقعی x:
x 1 = (c – 1 – ) و x 2 = (c – 1 + ).
در اینجا دو مورد ممکن است پیش بیاید:
حل نابرابری f(x)
f(x) با علامت c منطبق است. برای پاسخ به این سوال، توجه داشته باشید که - ، یعنی s – 1 – ˂ s – 1 + ، اما از آنجایی که s (s – 1 – ) (s - 1 + ) و بنابراین راه حل نابرابری به صورت زیر خواهد بود:
(- ؛ (s – 1 – )) ( (s – 1 + )؛ + ).
حال برای حل نابرابری کافی است مقادیری از c را مشخص کنیم که علامت f (x) مخالف علامت c است. از آنجایی که در 0 1 2، سپس x (x 1; x 2).
پاسخ: وقتی c = 0 x R;
با (- ; x 2 ) (x 1 ; + );
در 0 (x 1; x 2)؛
برای c 0.25 هیچ راه حلی وجود ندارد.
دیدگاه یک پارامتر به عنوان یک متغیر مساوی در روش های گرافیکی برای حل و نابرابری های درجه دوم منعکس می شود. در واقع، از آنجایی که پارامتر "در حقوق برابر" با متغیر است، طبیعی است که بتوان آن را به محور مختصات خود "تخصیص" کرد. بنابراین، یک صفحه مختصات (x; a) بوجود می آید. چنین جزئیات جزئی مانند کنار گذاشتن انتخاب سنتی حروف x و y برای نشان دادن محورها، یکی از مؤثرترین روش ها برای حل مسائل با پارامترها را تعیین می کند.
وقتی مشکل شامل یک پارامتر a و یک متغیر x باشد راحت است. خود فرآیند حل به صورت شماتیک شبیه به این است. ابتدا یک تصویر گرافیکی ساخته می شود، سپس، نمودار حاصل را با خطوط مستقیم عمود بر محور پارامتری قطع می کنیم، اطلاعات لازم را "حذف" می کنیم.
رد انتخاب سنتی حروف x و y برای تعیین محورها یکی از مؤثرترین روش ها برای حل مسائل با پارامترها - "روش دامنه" را تعیین می کند.
- روش شناسی برای حل نابرابری های درجه دوم در شرایط اولیه.
اجازه دهید یک راه حل تحلیلی برای یک نابرابری درجه دوم با پارامترها در نظر بگیریم که نتایج آن در خط اعداد در نظر گرفته می شود.
مثال 8.
تمام مقادیر x را پیدا کنید که برای هر کدام نابرابری است
(2x)a 2 +(x2 -2x+3)a-3x≥0
برای هر مقدار متعلق به بازه [-3;0] ارضا می شود.
راه حل. اجازه دهید سمت چپ این نابرابری را به صورت زیر تبدیل کنیم:
(2-x)a 2 + (x 2 -2x+3)a-3x=ax 2 - a 2 x - 2ax + 2a 2 + 3a - 3x =
تبر (x - a)-2a(x - a)- 3(x-a) = (x - a)(ax- 2a - 3).
این نابرابری به شکل زیر خواهد بود: (x - a) (ax - 2a - 3) ≥ 0.
اگر a = 0 باشد، می‌گیریم - Zx ≥ 0 x ≤ 0.
اگر a ≠ 0، آنگاه -3 a
چون الف 0، سپس راه حل این نابرابری، فاصله محور عددی واقع بین ریشه های معادله مربوط به نابرابری خواهد بود.
بیایید موقعیت نسبی اعداد را دریابیمیک و ، با در نظر گرفتن شرایط - 3 ≤ a
3 ≤a
A = -1.
اجازه دهید در همه موارد در نظر گرفته شده، راه حل های این نابرابری را بسته به مقادیر پارامتر ارائه کنیم:
دریافتیم که فقط x = -1 راه حلی برای این نابرابری برای هر مقدار از پارامتر a است .
پاسخ: -1
- نتیجه گیری
چرا پروژه ای با موضوع "توسعه توصیه های روش شناختی برای حل معادلات درجه دوم و نابرابری ها با پارامترها" انتخاب کردم؟ از آنجایی که هنگام حل معادلات مثلثاتی، نمایی، لگاریتمی، نابرابری ها، سیستم ها، اغلب معادلات و نابرابری های خطی و اغلب درجه دوم را در نظر می گیریم. هنگام حل مسائل پیچیده با پارامترها، اکثر وظایف با استفاده از تبدیل های معادل به انتخاب راه حل هایی از نوع کاهش می یابد: a (x – a) (x – c) > 0 (
ما مبنای نظری برای حل معادلات درجه دوم و نابرابری با پارامترها را بررسی کردیم. ما فرمول‌ها و تبدیل‌های لازم را به یاد آوردیم، به ترتیب‌های مختلف نمودارهای یک تابع درجه دوم بسته به مقدار متمایز، علامت ضریب پیشرو، محل ریشه‌ها و رئوس سهمی نگاه کردیم. ما طرحی را برای حل و انتخاب نتایج شناسایی کردیم و جدولی را تهیه کردیم.
این پروژه روش های تحلیلی و گرافیکی را برای حل معادلات درجه دوم و نابرابری ها نشان می دهد. دانش آموزان در یک مدرسه حرفه ای برای جذب بهتر مطالب به درک بصری از مطالب نیاز دارند. نشان داده می شود که چگونه می توان متغیر x را تغییر داد و پارامتر را به عنوان یک مقدار مساوی پذیرفت.
برای درک واضح این موضوع، راه حل 8 مسئله با پارامترها، 1 تا 2 برای هر بخش در نظر گرفته شده است. در مثال شماره 1، تعداد راه حل ها برای مقادیر مختلف پارامتر در نظر گرفته شده است. یک تصویر گرافیکی برای حل نابرابری های درجه دوم ساخته شده است. در مثال شماره 5 از روش جایگزینی یک پارامتر به عنوان مقدار مساوی استفاده شده است. این پروژه شامل در نظر گرفتن مثال شماره 8 از وظایف موجود در بخش C برای آماده سازی فشرده برای قبولی در آزمون یکپارچه دولتی است.
برای آموزش با کیفیت بالا دانش آموزان در حل مسائل با پارامترها، توصیه می شود به طور کامل از فن آوری های چند رسانه ای استفاده کنید، یعنی: از ارائه ها برای سخنرانی ها، کتاب های درسی الکترونیکی و کتاب ها و پیشرفت های خود از کتابخانه رسانه استفاده کنید. درس های باینری در ریاضی + علوم کامپیوتر بسیار موثر است. اینترنت یک دستیار ضروری برای معلمان و دانش آموزان است. ارائه به اشیاء وارد شده از منابع آموزشی موجود نیاز دارد. راحت ترین و قابل قبول ترین کار برای کار، مرکز "استفاده از مایکروسافت آفیس در مدرسه" است.
توسعه توصیه های روش شناختی در مورد این موضوع کار معلمان جوانی را که برای کار در مدرسه می آیند تسهیل می کند ، به کارنامه معلم اضافه می کند ، به عنوان الگویی برای موضوعات خاص عمل می کند و راه حل های نمونه به دانش آموزان کمک می کند تا با وظایف پیچیده کنار بیایند.
- ادبیات.
1. گورنشتاین پی.آی.، پولونسکی وی.بی.، یاکیر ام.اس. مشکل در پارامترها "Ilexa"، "Gymnasium"، مسکو - خارکف، 2002.
2. بالایان ای.ن. مجموعه ای از مسائل ریاضی برای آمادگی برای آزمون دولتی و المپیادهای یکپارچه. پایه های 9-11. "ققنوس"، روستوف-آن-دون، 2010.
3. Yastrebinetsky G.A. مشکل در پارامترها م.، "روشنگری"، 1365.
4. Kolesnikova S.I. ریاضیات. حل مسائل پیچیده آزمون دولتی واحد. M. "IRIS - Press"، 2005.
5. Rodionov E.M., Sinyakova S.L. ریاضیات. راهنمای متقاضیان ورود به دانشگاه. مرکز آموزشی "Orientir" MSTU به نام. N.E. باومن، ام.، 2004.
6. اسکانوی م.ی. مجموعه مسائل ریاضی برای ورودی های دانشگاه: در 2 کتاب. کتاب 1، م.، 2009.
