چه زوایایی در ذوزنقه مساوی است؟ ذوزنقه

"تأیید شده"

رئیس یک رشته جداگانه

(ریاضیات، علوم کامپیوتر و ICT)

یو. وی کریلوا ____________

"___" _____________ 2015

« ذوزنقه و خواص آن»

توسعه روش شناختی

معلم ریاضی

شاتالینا النا دیمیتریونا

بررسی شده و

در جلسه PMO مورخ _________________

شماره پروتکل ______

مسکو

2015

فهرست مطالب

مقدمه 2

تعاریف 3

خواص ذوزنقه متساوی الساقین 4

دایره های محاطی و محصور 7

خصوصیات ذوزنقه های منقوش و محصور ۸

مقادیر متوسط ​​در ذوزنقه 12

خواص ذوزنقه دلخواه ۱۵

علائم ذوزنقه 18

سازه های اضافی در ذوزنقه 20

ناحیه ذوزنقه 25

10. نتیجه گیری

فهرست ادبیات استفاده شده

برنامه

شواهد برخی از خواص ذوزنقه 27

وظایف برای کار مستقل

مشکلات در موضوع "ذوزنقه" با افزایش پیچیدگی

تست غربالگری با موضوع ذوزنقه

مقدمه

این اثر به شکل هندسی به نام ذوزنقه اختصاص دارد. شما می گویید «یک چهره معمولی»، اما اینطور نیست. این مملو از رازها و رازهای زیادی است که اگر دقیق تر به آن نگاه کنید، چیزهای جدیدی را در دنیای هندسه کشف خواهید کرد که قبلاً حل نشده اند.

ذوزنقه - کلمه یونانی trapezion - "جدول". قرض گرفتن در قرن 18 از لات زبان، جایی که ذوزنقه یونانی است. چهارضلعی است که دو ضلع مقابل آن موازی هستند. ذوزنقه اولین بار توسط دانشمند یونانی باستان پوزیدونیوس (قرن دوم قبل از میلاد) مواجه شد. در زندگی ما چهره های متفاوتی وجود دارد. در کلاس هفتم با مثلث از نزدیک در کلاس هشتم آشنا شدیم، طبق برنامه درسی مدرسه شروع به مطالعه ذوزنقه کردیم. این رقم برای ما جالب بود و در کتاب درسی به طور غیر قابل قبولی در مورد آن نوشته شده است. بنابراین تصمیم گرفتیم این موضوع را در دست بگیریم و اطلاعاتی در مورد ذوزنقه پیدا کنیم. خواص آن

این کار به بررسی ویژگی‌هایی می‌پردازد که دانش‌آموزان از مطالبی که در کتاب درسی پوشش داده شده است آشنا هستند، اما عمدتاً ویژگی‌های ناشناخته‌ای را که برای حل مسائل پیچیده ضروری هستند، بررسی می‌کند. هرچه تعداد مشکلات حل شده بیشتر باشد، هنگام حل آنها سؤالات بیشتری ایجاد می شود. پاسخ به این پرسش‌ها گاهی مانند یک راز به نظر می‌رسد که با یادگیری ویژگی‌های جدید ذوزنقه، روش‌های غیرعادی برای حل مسائل و همچنین تکنیک ساخت‌های اضافی، به تدریج اسرار ذوزنقه را کشف می‌کنیم. در اینترنت، اگر آن را در یک موتور جستجو تایپ کنید، ادبیات بسیار کمی در مورد روش های حل مسائل در مورد موضوع "ذوزنقه" وجود دارد. در فرآیند کار روی پروژه، اطلاعات زیادی پیدا شد که به دانش آموزان در مطالعه عمیق هندسه کمک می کند.

ذوزنقه.

تعاریف

ذوزنقه - چهار ضلعی که فقط یک جفت ضلع آن موازی باشد (و جفت ضلع دیگر موازی نباشد).

اضلاع موازی ذوزنقه نامیده می شوددلایل .
دو تای دیگر طرفین هستنداگر اضلاع مساوی باشند به آن ذوزنقه می گویند

متساوی الساقینذوزنقه ای که در اضلاع آن زوایای قائمه دارد نامیده می شود

مستطیل شکلپاره ای که نقاط میانی اضلاع را به هم وصل می کند نامیده می شود.

خط وسط ذوزنقه

2 فاصله بین پایه ها را ارتفاع ذوزنقه می گویند.

3. خواص ذوزنقه متساوی الساقین

4

1
. قطرهای ذوزنقه متساوی الساقین برابر است.

0. برآمدگی ضلع جانبی ذوزنقه متساوی الساقین بر روی قاعده بزرگتر برابر است با نصف اختلاف پایه ها و برآمدگی مورب برابر با مجموع قاعده ها است.

3. دایره منقوش و محصور

اگر مجموع قاعده های ذوزنقه ای برابر با مجموع اضلاع باشد، می توان دایره ای را در آن حک کرد.
E

اگر ذوزنقه متساوی الساقین باشد، می توان دور آن دایره ای توصیف کرد.

4. خواص ذوزنقه های کتیبه و محصور

2. اگر بتوان دایره ای را در ذوزنقه متساوی الساقین حک کرد، پس

4 . مجموع طول پایه ها برابر است با مجموع طول اضلاع. بنابراین طول ضلع برابر با طول خط وسط ذوزنقه است.

اگر دایره ای در ذوزنقه حک شده باشد، اضلاع از مرکز آن با زاویه 90 درجه قابل مشاهده است. اگر دایره ای در ذوزنقه حک شود و یکی از اضلاع آن را لمس کند، آن را به قطعات تقسیم می کند.متر , و n

1

0 سپس شعاع دایره محاطی برابر با میانگین هندسی این قطعات است.

. اگر دایره ای به اندازه قطر روی پایه کوچکتر ذوزنقه ساخته شود، از وسط مورب ها عبور کند و پایه پایینی را لمس کند، زوایای ذوزنقه 30 درجه، 30 درجه، 150 درجه، 150 درجه است.

5. مقادیر متوسط ​​در ذوزنقه

میانگین هندسی در هر ذوزنقه با پایه الف و ب برای > الفب :

نابرابری درست است

6. خواص ذوزنقه دلخواه

1
. نقاط وسط قطرهای ذوزنقه و وسط اضلاع کناری روی یک خط مستقیم قرار دارند.

نقطه تلاقی ادامه اضلاع ذوزنقه دلخواه، نقطه تقاطع مورب های آن و نقاط میانی پایه ها روی یک خط مستقیم قرار دارند.

6. مجموع مربعات قطرهای ذوزنقه دلخواه برابر است با مجموع مربعات اضلاع جانبی که به دو برابر حاصلضرب قاعده ها اضافه می شود.

د 1 2 + د 2 2 = ج 2 + د 2 + 2 ab

7
. در یک ذوزنقه مستطیلی، اختلاف مربعات مورب برابر است با اختلاف مربع های پایه ها. د 1 2 - د 2 2 = در هر ذوزنقه با پایه 2 – و 2

8 . خطوط مستقیمی که اضلاع یک زاویه را قطع می کنند، بخش های متناسب را از دو طرف زاویه قطع می کنند.

9. قسمتی که به موازات پایه ها است و از نقطه تقاطع مورب ها می گذرد توسط دومی به نصف تقسیم می شود.

7. علائم ذوزنقه

8. سازه های اضافی در ذوزنقه

1. پاره ای که نقاط میانی اضلاع را به هم وصل می کند، خط وسط ذوزنقه است.

2
. قطعه ای به موازات یکی از اضلاع جانبی ذوزنقه که یک سر آن با وسط ضلع جانبی دیگر منطبق است و دیگری متعلق به خط مستقیم حاوی قاعده است.

3
. اگر تمام اضلاع ذوزنقه داده شود، یک خط مستقیم به موازات ضلع از طریق راس قاعده کوچکتر کشیده می شود. نتیجه یک مثلث با اضلاع برابر با اضلاع جانبی ذوزنقه و اختلاف در پایه ها است. با استفاده از فرمول هرون مساحت مثلث و سپس ارتفاع مثلث را که برابر با ارتفاع ذوزنقه است را پیدا کنید.

4

. ارتفاع یک ذوزنقه متساوی الساقین که از راس قاعده کوچکتر کشیده شده است، قاعده بزرگتر را به قطعاتی تقسیم می کند که یکی از آنها برابر با نصف اختلاف پایه ها و دیگری برابر با نصف مجموع پایه های ذوزنقه است. یعنی خط وسط ذوزنقه.

5. ارتفاع ذوزنقه که از رئوس یک پایه پایین می آید، بر روی یک خط مستقیم که پایه دیگر را در بر می گیرد، قطعه ای برابر با پایه اول بریده می شود.

6
. یک قطعه موازی با یکی از مورب های ذوزنقه از طریق یک راس کشیده می شود - نقطه ای که انتهای مورب دیگر است. حاصل مثلثی است که دو ضلع آن برابر با قطرهای ذوزنقه و ضلع سوم برابر با مجموع قاعده هاست.

7
.قطعه اتصال نقاط وسط قطرها برابر است با نصف اختلاف پایه های ذوزنقه.

8. نیمسازهای زوایای مجاور یکی از اضلاع جانبی ذوزنقه عمود بر هم هستند و در نقطه ای که روی خط وسط ذوزنقه قرار دارد، قطع می کنند، یعنی وقتی آنها را قطع می کنند، مثلث قائم الزاویه ای با هیپوتانوس برابر با جانبی تشکیل می شود. سمت

9. نیمساز یک زاویه ذوزنقه، مثلث متساوی الساقین را قطع می کند.

1
0. قطرهای یک ذوزنقه دلخواه هنگام قطع، دو مثلث مشابه با ضریب تشابه برابر با نسبت قاعده ها و دو مثلث مساوی در مجاورت اضلاع جانبی تشکیل می دهند.

1
1. قطرهای یک ذوزنقه دلخواه هنگام قطع، دو مثلث مشابه با ضریب تشابه برابر با نسبت پایه ها و دو مثلث مساوی در مجاورت اضلاع جانبی تشکیل می دهند.

1
2. ادامه اضلاع ذوزنقه تا تقاطع امکان در نظر گرفتن مثلث های مشابه را فراهم می کند.

13. اگر دایره ای در ذوزنقه متساوی الساقین حک شده باشد، ارتفاع ذوزنقه را محاسبه کنید - میانگین هندسی حاصلضرب پایه های ذوزنقه یا دو برابر میانگین هندسی حاصلضرب قطعات ضلع جانبی که در آن قرار دارد. بر نقطه مماس تقسیم می شود.

9. مساحت ذوزنقه

1 . مساحت ذوزنقه برابر است با حاصل ضرب نصف مجموع قاعده ها و ارتفاع اس = ½( برای + الف) ساعتیا

پ

مساحت ذوزنقه برابر است با حاصلضرب خط وسط ذوزنقه و ارتفاع آن. اس = اگر دایره ای در ذوزنقه حک شود و یکی از اضلاع آن را لمس کند، آن را به قطعات تقسیم می کند. ساعت .

2. مساحت ذوزنقه برابر است با حاصلضرب یک ضلع و یک عمود از وسط ضلع دیگر به خط حاوی ضلع اول.

مساحت ذوزنقه متساوی الساقین با شعاع دایره محاطی برابر است rو زاویه در پایهα :

10. نتیجه گیری

از ذوزنقه در کجا، چگونه و برای چه استفاده می شود؟

ذوزنقه در ورزش: ذوزنقه مطمئناً اختراع مترقی بشر است. این طراحی شده است تا دستان ما را تسکین دهد و موج سواری را به استراحتی راحت و آسان تبدیل کند. راه رفتن روی یک تخته کوتاه بدون ذوزنقه اصلاً معنی ندارد، زیرا بدون آن نمی توان به درستی کشش را بین پله و پاها تقسیم کرد و به طور موثر شتاب داد.

ذوزنقه در مد: ذوزنقه در لباس در قرون وسطی، در دوران رومانس در قرن 9 تا 11 رایج بود. در آن زمان، اساس لباس های زنانه، تونیک های بلندی به سمت پایین بود، تونیک به شدت گسترش یافت که یک جلوه ذوزنقه ای ایجاد کرد. احیای سیلوئت در سال 1961 اتفاق افتاد و به سرود جوانی، استقلال و پیچیدگی تبدیل شد. مدل شکننده لزلی هورنبی، معروف به توئیگی، نقش بزرگی در محبوبیت این ذوزنقه ایفا کرد. دختری کوتاه قد با هیکلی بی اشتها و چشمان درشت به نماد آن دوران تبدیل شد و لباس های مورد علاقه او لباس های کوتاه خط الف بود.

ذوزنقه در طبیعت: ذوزنقه در طبیعت نیز یافت می شود. انسان ها ماهیچه ذوزنقه ای دارند و برخی افراد صورت ذوزنقه ای شکل دارند. گلبرگ های گل، صورت های فلکی و البته کوه کلیمانجارو نیز شکل ذوزنقه ای دارند.

ذوزنقه در زندگی روزمره: از ذوزنقه در زندگی روزمره نیز استفاده می شود، زیرا شکل آن کاربردی است. در اشیایی مانند: سطل بیل مکانیکی، میز، پیچ، ماشین یافت می شود.

ذوزنقه نمادی از معماری اینکاها است. فرم سبک غالب در معماری اینکاها ساده اما برازنده است - ذوزنقه. این نه تنها اهمیت کاربردی دارد، بلکه طراحی هنری به شدت محدودی دارد. درگاه‌ها، پنجره‌ها و طاقچه‌های دیواری ذوزنقه‌ای در انواع ساختمان‌ها، هم در معابد و هم در ساختمان‌های کوچک‌تر با ساختمان‌های خشن‌تر یافت می‌شوند. ذوزنقه در معماری مدرن نیز یافت می شود. این شکل از ساختمان ها غیر معمول است، بنابراین چنین ساختمان هایی همیشه چشم عابران را به خود جلب می کنند.

ذوزنقه در فناوری: ذوزنقه در طراحی قطعات در فناوری فضایی و هوانوردی استفاده می شود. به عنوان مثال، برخی از پنل های خورشیدی در ایستگاه های فضایی مانند ذوزنقه شکل می گیرند زیرا مساحت زیادی دارند، به این معنی که انرژی خورشیدی بیشتری را جمع می کنند.

در قرن بیست و یکم، مردم عملاً دیگر به معنای اشکال هندسی در زندگی خود فکر نمی کنند. آنها اصلاً برایشان مهم نیست که میز، عینک یا تلفنشان چه شکلی است. آنها به سادگی فرمی را انتخاب می کنند که کاربردی باشد. اما استفاده از شی، هدف آن و نتیجه کار ممکن است به شکل این یا آن چیز بستگی داشته باشد. امروز شما را با یکی از بزرگترین دستاوردهای بشر - ذوزنقه - آشنا کردیم. ما در را به دنیای شگفت انگیز فیگورها باز کردیم، اسرار ذوزنقه را به شما گفتیم و به شما نشان دادیم که هندسه در اطراف ما وجود دارد.

فهرست ادبیات استفاده شده

Bolotov A.A.، Prokhorenko V.I.، Safonov V.F.، ریاضیات نظریه و مسائل. کتاب 1 راهنمای مطالعه برای متقاضیان M.1998 انتشارات MPEI.

Bykov A.A.، Malyshev G.Yu.، GUVS دانشکده آموزش پیش دانشگاهی. ریاضیات. راهنمای آموزشی و روش شناختی 4 قسمت M2004

گوردین آر.ک. پلان سنجی. کتاب مسائل.

ایوانف A.A. ایوانف A.P.، ریاضیات: راهنمای آماده سازی برای آزمون دولتی واحد و پذیرش در دانشگاه ها - M: انتشارات MIPT، 2003-288p. شابک 5-89155-188-3

Pigolkina T.S.، وزارت آموزش و پرورش و علوم فدراسیون روسیه، مؤسسه آموزشی بودجه دولت فدرال آموزش تکمیلی برای کودکان "موسسه فیزیک و فناوری ZFTSH مسکو (دانشگاه دولتی)". ریاضیات. پلان سنجی. تکالیف شماره 2 برای پایه دهم (سال تحصیلی 92-1391).

Pigolkina T.S., Planimetry (قسمت 1) دایره المعارف ریاضی ورودی. M.، انتشارات دانشگاه آزاد روسیه 1992.

شاریگین I.F. مسائل منتخب در هندسه برای امتحانات رقابتی در دانشگاه ها (1987-1990) مجله Lvov "Quantor" 1991.

دایره المعارف "آوانتا پلاس"، ریاضیات ام.، دنیای دایره المعارف ها آوانتا 2009.

برنامه

1. اثبات برخی از خواص ذوزنقه.

1. خط مستقیمی که از نقطه تقاطع قطرهای ذوزنقه موازی با پایه های آن می گذرد، اضلاع جانبی ذوزنقه را در نقاط قطع می کند.ک و L . ثابت کنید که اگر پایه های ذوزنقه مساوی است الف الف و ، آن طول قطعه KL برابر با میانگین هندسی قاعده ذوزنقه است. اثبات

اجازه دهیددر مورد - نقطه تقاطع مورب ها،پس از میلاد = الف، خورشید = و . مستقیم KL به موازات پایهپس از میلاد از این رو،ک در مورد║ پس از میلاد , مثلث هادر ک در مورد وبد بنابراین مشابه هستند

(1)

(2)

بیایید (2) را به (1) جایگزین کنیم، دریافت می کنیم KO =

به همین ترتیب L.O.= سپس ک L = K.O. + L.O. =

در برای هر ذوزنقه ای، نقطه وسط پایه ها، نقطه تلاقی مورب ها و نقطه تلاقی ادامه اضلاع جانبی روی یک خط مستقیم قرار می گیرند.

اثبات: اجازه دهید امتداد اضلاع در نقطه قطع شوندبه از طریق نقطهبه و دورهدر مورد تقاطع های مورببیایید یک خط مستقیم بکشیم CO.

ک

اجازه دهید ثابت کنیم که این خط پایه ها را به نصف تقسیم می کند.

در مورد قابل توجه استVM = x، ام اس = y، AN = و، ND = v . ما داریم:

∆ VKM ~ ∆AKN →

م

x

ب

سی

Y

دایره محصور و ذوزنقه. سلام! یک نشریه دیگر برای شما وجود دارد که در آن به مشکلات ذوزنقه ها خواهیم پرداخت. تکالیف بخشی از امتحان ریاضی است. در اینجا آنها در یک گروه ترکیب می شوند، نه تنها یک ذوزنقه، بلکه ترکیبی از اجسام - یک ذوزنقه و یک دایره. اکثر این مشکلات به صورت شفاهی حل می شوند. اما مواردی نیز وجود دارند که باید به آنها توجه ویژه ای شود، به عنوان مثال، وظیفه 27926.

چه نظریه ای را باید به خاطر بسپارید؟ این:

مشکلات ذوزنقه ای که در وبلاگ موجود است قابل مشاهده است اینجا.

27924. یک دایره در اطراف یک ذوزنقه توصیف شده است. محیط ذوزنقه 22 و خط وسط 5 است. ضلع ذوزنقه را پیدا کنید.

توجه داشته باشید که یک دایره را فقط می توان در اطراف یک ذوزنقه متساوی الساقین توصیف کرد. خط وسط به ما داده می شود، به این معنی که می توانیم مجموع پایه ها را تعیین کنیم، یعنی:

این به این معنی است که مجموع اضلاع برابر با 22-10 = 12 (محیط منهای پایه) خواهد بود. از آنجایی که اضلاع ذوزنقه متساوی الساقین برابر است، یک ضلع آن برابر با شش خواهد بود.

27925. ضلع جانبی ذوزنقه متساوی الساقین برابر با قاعده کوچکتر آن است، زاویه قاعده 60 0، قاعده بزرگتر 12 است. شعاع محیطی این ذوزنقه را بیابید.

اگر با یک دایره و یک شش ضلعی که در آن حک شده است مشکلات را حل کنید، بلافاصله پاسخ را صدا خواهید کرد - شعاع 6 است. چرا؟

نگاه کنید: یک ذوزنقه متساوی الساقین با زاویه پایه برابر با 60 0 و اضلاع مساوی AD، DC و CB، نیمی از یک شش ضلعی منظم است:

در چنین شش ضلعی، بخش اتصال رئوس مخالف از مرکز دایره عبور می کند. *مرکز شش ضلعی و مرکز دایره منطبق هستند، جزئیات بیشتر

یعنی پایه بزرگتر این ذوزنقه با قطر دایره محصور منطبق است. بنابراین شعاع شش است.

*البته می توان برابری مثلث های ADO، DOC و OCB را در نظر گرفت. ثابت کنید که آنها متساوی الاضلاع هستند. سپس نتیجه بگیرید که زاویه AOB برابر با 180 0 است و نقطه O از رئوس A، D، C و B مساوی فاصله دارد و بنابراین AO=OB=12/2=6.

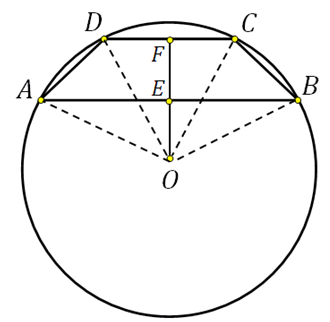
27926. قاعده ذوزنقه متساوی الساقین 8 و 6 است. شعاع دایره محدود شده 5 است. ارتفاع ذوزنقه را بیابید.

توجه داشته باشید که مرکز دایره محصور شده روی محور تقارن قرار دارد و اگر ارتفاع ذوزنقه ای را که از این مرکز می گذرد بسازیم، وقتی با پایه ها تلاقی می کند آنها را به دو نیم تقسیم می کند. بیایید این را در طرح نشان دهیم و همچنین مرکز را به رئوس متصل کنیم:

قطعه EF ارتفاع ذوزنقه است، باید آن را پیدا کنیم.

در مثلث قائم الزاویه OFC ما هیپوتنوس (این شعاع دایره است)، FC=3 (از DF=FC) می دانیم. با استفاده از قضیه فیثاغورث می توانیم OF را محاسبه کنیم:

در مثلث قائم الزاویه OEB، هیپوتنوس (این شعاع دایره است)، EB=4 (از AE=EB) می دانیم. با استفاده از قضیه فیثاغورث می توانیم OE را محاسبه کنیم:

بنابراین EF=FO+OE=4+3=7.

حالا یک نکته مهم!

در این مسئله، شکل به وضوح نشان می دهد که پایه ها در طرفین مخالف مرکز دایره قرار دارند، بنابراین مشکل به این ترتیب حل می شود.

اگر شرایط شامل طرحی نبود چه؟

آن وقت مشکل دو جواب خواهد داشت. چرا؟ با دقت نگاه کنید - دو ذوزنقه با پایه های داده شده را می توان در هر دایره ای حک کرد:

*یعنی با توجه به پایه های ذوزنقه و شعاع دایره دو ذوزنقه وجود دارد.

و راه حل "گزینه دوم" به شرح زیر خواهد بود.

با استفاده از قضیه فیثاغورث، OF را محاسبه می کنیم:

بیایید OE را نیز محاسبه کنیم:

بنابراین EF=FO–OE=4–3=1.

البته در یک مسئله با پاسخ کوتاه در آزمون یکپارچه دولتی نمی توان دو پاسخ داشت و مشکل مشابه بدون طرح داده نمی شود. بنابراین، به طرح توجه ویژه ای داشته باشید! یعنی: پایه های ذوزنقه چگونه قرار گرفته اند. اما در وظایف با پاسخ دقیق، این در سال های گذشته وجود داشت (با شرایط کمی پیچیده تر). هر کسی که تنها یک گزینه را برای مکان ذوزنقه در نظر می گرفت، یک امتیاز را در این کار از دست داد.

27937. یک ذوزنقه دور دایره ای محصور شده است که محیط آن 40 است. خط وسط آن را پیدا کنید.

در اینجا باید فوراً خاصیت یک چهارضلعی را که پیرامون یک دایره محصور شده است، یادآوری کنیم:

مجموع اضلاع مقابل هر چهار ضلعی که دور یک دایره محصور شده است برابر است.

حفظ حریم خصوصی شما برای ما مهم است. به همین دلیل، ما یک خط مشی رازداری ایجاد کرده ایم که نحوه استفاده و ذخیره اطلاعات شما را شرح می دهد. لطفاً رویه‌های حفظ حریم خصوصی ما را مرور کنید و اگر سؤالی دارید با ما در میان بگذارید.

جمع آوری و استفاده از اطلاعات شخصی

اطلاعات شخصی به داده هایی اشاره دارد که می توان از آنها برای شناسایی یا تماس با یک فرد خاص استفاده کرد.

ممکن است در هر زمانی که با ما تماس می گیرید از شما خواسته شود اطلاعات شخصی خود را ارائه دهید.

در زیر چند نمونه از انواع اطلاعات شخصی که ممکن است جمع آوری کنیم و نحوه استفاده از این اطلاعات آورده شده است.

چه اطلاعات شخصی جمع آوری می کنیم:

• هنگامی که درخواستی را در سایت ارسال می کنید، ممکن است اطلاعات مختلفی از جمله نام، شماره تلفن، آدرس ایمیل و غیره شما را جمع آوری کنیم.

نحوه استفاده ما از اطلاعات شخصی شما:

• اطلاعات شخصی که جمع آوری می کنیم به ما امکان می دهد با پیشنهادات منحصر به فرد، تبلیغات و سایر رویدادها و رویدادهای آینده با شما تماس بگیریم.
• هر از گاهی، ممکن است از اطلاعات شخصی شما برای ارسال اعلان‌ها و ارتباطات مهم استفاده کنیم.
• ما همچنین ممکن است از اطلاعات شخصی برای مقاصد داخلی مانند انجام ممیزی، تجزیه و تحلیل داده ها و تحقیقات مختلف به منظور بهبود خدمات ارائه شده و ارائه توصیه هایی در مورد خدمات خود به شما استفاده کنیم.
• اگر در قرعه کشی جوایز، مسابقه یا تبلیغات مشابه شرکت می کنید، ممکن است از اطلاعاتی که شما ارائه می دهید برای اجرای چنین برنامه هایی استفاده کنیم.

افشای اطلاعات به اشخاص ثالث

ما اطلاعات دریافتی از شما را در اختیار اشخاص ثالث قرار نمی دهیم.

استثنائات:

• در صورت لزوم - مطابق با قانون، رویه قضایی، در مراحل قانونی و / یا بر اساس درخواست های عمومی یا درخواست های ارگان های دولتی در فدراسیون روسیه - اطلاعات شخصی خود را افشا کنید. همچنین اگر تشخیص دهیم که چنین افشایی برای اهداف امنیتی، اجرای قانون یا سایر اهداف مهم عمومی ضروری یا مناسب است، ممکن است اطلاعاتی درباره شما فاش کنیم.
• در صورت سازماندهی مجدد، ادغام یا فروش، ممکن است اطلاعات شخصی را که جمع آوری می کنیم به شخص ثالث جانشین مربوطه منتقل کنیم.

حفاظت از اطلاعات شخصی

ما اقدامات احتیاطی - از جمله اداری، فنی و فیزیکی - را برای محافظت از اطلاعات شخصی شما در برابر از دست دادن، سرقت، و سوء استفاده، و همچنین دسترسی غیرمجاز، افشا، تغییر و تخریب انجام می دهیم.

احترام به حریم خصوصی شما در سطح شرکت

برای اطمینان از ایمن بودن اطلاعات شخصی شما، استانداردهای حریم خصوصی و امنیتی را به کارمندان خود ابلاغ می کنیم و شیوه های حفظ حریم خصوصی را به شدت اجرا می کنیم.

\[(\Large(\text(ذوزنقه آزاد)))\]

تعاریف

ذوزنقه یک چهارضلعی محدب است که دو ضلع آن موازی و دو ضلع دیگر موازی نیستند.

اضلاع موازی ذوزنقه را قاعده و دو ضلع دیگر را اضلاع آن می نامند.

ارتفاع ذوزنقه عمودی است که از هر نقطه یک قاعده به قاعده دیگر نزول می کند.

قضایا: خواص ذوزنقه

1) مجموع زوایای ضلع \(180^\circ\) است.

2) مورب ها ذوزنقه را به چهار مثلث تقسیم می کنند که دو تای آنها شبیه به هم و دو تای دیگر از نظر اندازه مساوی هستند.

اثبات

1) زیرا \(AD\موازی BC\)، سپس زوایا \(\زاویه BAD\) و \(\زاویه ABC\) برای این خطوط و عرضی \(AB\) یک طرفه هستند، بنابراین، \(\ زاویه BAD +\ زاویه ABC=180^\circ\).

2) چون \(AD\parallel BC\) و \(BD\) یک سکانس هستند، سپس \(\angle DBC=\angle BDA\) بصورت متقاطع قرار می گیرند.
همچنین \(\angle BOC=\angle AOD\) به صورت عمودی.
بنابراین، در دو زاویه \(\ مثلث BOC \sim \مثلث AOD\).

این را ثابت کنیم \(S_(\مثلث AOB)=S_(\مثلث COD)\). فرض کنید \(h\) ارتفاع ذوزنقه باشد. سپس \(S_(\مثلث ABD)=\frac12\cdot h\cdot AD=S_(\مثلث ACD)\). سپس: \

تعریف

خط وسط یک ذوزنقه قطعه ای است که نقاط میانی اضلاع را به هم متصل می کند.

قضیه

خط وسط ذوزنقه موازی قاعده ها و برابر با نیم جمع آنهاست.

اثبات*

1) بیایید موازی بودن را ثابت کنیم.

اجازه دهید از طریق نقطه \(M\) خط مستقیم \(MN"\parallel AD\) (\(N"\in CD\)) را رسم کنیم. سپس، طبق قضیه تالس (از آنجا که \(MN"\parallel AD\parallel BC, AM=MB\)) نقطه \(N"\) وسط بخش \(CD\) است. این بدان معنی است که نقاط \(N\) و \(N"\) بر هم منطبق خواهند شد.

2) بیایید فرمول را ثابت کنیم.

بیایید \(BB"\perp AD, CC"\perp AD\) را انجام دهیم. اجازه دهید \(BB"\cap MN=M، CC"\cap MN=N"\).

سپس بر اساس قضیه تالس، \(M"\) و \(N"\) به ترتیب نقاط میانی پاره های \(BB"\) و \(CC"\) هستند. این بدان معناست که \(MM"\) خط وسط \(\مثلث ABB"\) است ، \(NN"\) خط وسط \(\مثلث DCC"\) است. به همین دلیل: \

چون \(MN\parallel AD\parallel BC\)و \(BB، CC"\perp AD\)، سپس \(B"M"N"C"\) و \(BM"N"C\) مستطیل هستند. با توجه به قضیه تالس، از \(MN\موازی AD\) و \(AM=MB\) نتیجه می‌شود که \(B"M"=M"B\) از این رو \(B"M"N"C "\) و \(BM"N"C\) مستطیل های مساوی هستند، بنابراین، \(M"N"=B"C"=BC\) .

بدین ترتیب:

\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\راست)\]

قضیه: خاصیت ذوزنقه دلخواه

نقاط میانی پایه ها، نقطه تلاقی قطرهای ذوزنقه و نقطه تلاقی امتداد اضلاع جانبی روی یک خط مستقیم قرار دارند.

اثبات*
توصیه می شود پس از مطالعه مبحث "شباهت مثلث ها" با اثبات آشنا شوید.

1) اجازه دهید ثابت کنیم که نقاط \(P\)، \(N\) و \(M\) روی یک خط قرار دارند.

بیایید یک خط مستقیم رسم کنیم \(PN\) (\(P\) نقطه تقاطع امتداد اضلاع جانبی است، \(N\) وسط \(BC\) است). اجازه دهید ضلع \(AD\) را در نقطه \(M\) قطع کند. اجازه دهید ثابت کنیم که \(M\) نقطه وسط \(AD\) است.

\(\triangle BPN\) و \(\triangle APM\) را در نظر بگیرید. آنها در دو زاویه مشابه هستند (\(\ زاویه APM\) - کلی، \(\زاویه PAM=\زاویه PBN\) مطابق با \(AD\ موازی BC\) و \(AB\) secant). یعنی: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]

\(\مثلث CPN\) و \(\مثلث DPM\) را در نظر بگیرید. آنها در دو زاویه مشابه هستند (\(\زاویه DPM\) - عمومی، \(\زاویه PDM=\زاویه PCN\) مطابق با \(AD\ موازی BC\) و \(CD\) secant). یعنی: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]

از اینجا \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). اما \(BN=NC\) بنابراین \(AM=DM\) .

2) اجازه دهید ثابت کنیم که نقاط \(N, O, M\) روی یک خط قرار دارند.

فرض کنید \(N\) نقطه وسط \(BC\) و \(O\) نقطه تقاطع قطرها باشد. بیایید یک خط مستقیم \(NO\) رسم کنیم، ضلع \(AD\) را در نقطه \(M\) قطع می کند. اجازه دهید ثابت کنیم که \(M\) نقطه وسط \(AD\) است.

\(\مثلث BNO\sim \مثلث DMO\)در امتداد دو زاویه (\(\زاویه OBN=\زاویه ODM\) به صورت متقاطع در \(BC\موازی AD\) و \(BD\) سکونت؛ \(\زاویه BON=\زاویه DOM\) به صورت عمودی). یعنی: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]

به همین ترتیب \(\triangle CON\sim \triangle AOM\). یعنی: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]

از اینجا \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). اما \(BN=CN\) بنابراین \(AM=MD\) .

\[(\Large(\text(ذوزنقه متساوی الساقین)))\]

تعاریف

ذوزنقه در صورتی مستطیل نامیده می شود که یکی از زوایای آن قائمه باشد.

ذوزنقه اگر اضلاع آن مساوی باشد متساوی الساقین نامیده می شود.

قضایا: خواص ذوزنقه متساوی الساقین

1) ذوزنقه متساوی الساقین دارای زوایای قاعده مساوی است.

2) قطرهای ذوزنقه متساوی الساقین برابر است.

3) دو مثلث که از مورب و یک قاعده تشکیل شده اند متساوی الساقین هستند.

اثبات

1) ذوزنقه متساوی الساقین \(ABCD\) را در نظر بگیرید.

از رئوس \(B\) و \(C\) عمودهای \(BM\) و \(CN\) را به ترتیب به ضلع \(AD\) رها می کنیم. از آنجایی که \(BM\perp AD\) و \(CN\perp AD\) , سپس \(BM\perp CN\) ; \(AD\parallel BC\)، سپس \(MBCN\) متوازی الاضلاع است، بنابراین \(BM = CN\) .

مثلث های قائم الزاویه \(ABM\) و \(CDN\) را در نظر بگیرید. از آنجایی که هیپوتنوس آنها برابر است و پایه \(BM\) برابر با پایه \(CN\) است، پس این مثلث ها برابر هستند، بنابراین \(\زاویه DAB = \زاویه CDA\) .

2)

چون \(AB=CD، \زاویه A=\زاویه D، AD\)- عمومی، سپس طبق علامت اول. بنابراین، \(AC=BD\) .

3) زیرا \(\مثلث ABD=\مثلث ACD\)، سپس \(\angle BDA=\angle CAD\) . بنابراین، مثلث \(\مثلث AOD\) متساوی الساقین است. به طور مشابه، ثابت شده است که \(\مثلث BOC\) متساوی الساقین است.

قضایا: علائم ذوزنقه متساوی الساقین

1) اگر ذوزنقه ای دارای زوایای قاعده مساوی باشد، متساوی الساقین است.

2) اگر ذوزنقه قطرهای مساوی داشته باشد، متساوی الساقین است.

اثبات

ذوزنقه \(ABCD\) را طوری در نظر بگیرید که \(\زاویه A = \زاویه D\) .

اجازه دهید مانند شکل ذوزنقه را به مثلث \(AED\) کامل کنیم. از آنجایی که \(\ زاویه 1 = \زاویه 2\) ، پس مثلث \(AED\) متساوی الساقین و \(AE = ED\) است. زوایای \(1\) و \(3\) به عنوان زوایای متناظر برای خطوط موازی \(AD\) و \(BC\) و عرضی \(AB\) برابر هستند. به طور مشابه، زوایای \(2\) و \(4\) برابر هستند، اما \(\زاویه 1 = \زاویه 2\) \(\ زاویه 3 = \ زاویه 1 = \ زاویه 2 = \ زاویه 4\)بنابراین، مثلث \(BEC\) نیز متساوی الساقین و \(BE = EC\) است.

در پایان \(AB = AE - BE = DE - CE = CD\)یعنی \(AB = CD\) که باید ثابت شود.

2) اجازه دهید \(AC=BD\) . چون \(\مثلث AOD\sim \مثلث BOC\)، سپس ضریب شباهت آنها را با \(k\) نشان می دهیم. سپس اگر \(BO=x\) ، آنگاه \(OD=kx\) . مشابه \(CO=y \Rightarrow AO=ky\) .

چون \(AC=BD\)، سپس \(x+kx=y+ky \Rightarrow x=y\) . این بدان معنی است که \(\مثلث AOD\) متساوی الساقین است و \(\ زاویه OAD=\زاویه ODA\) .

بنابراین با توجه به اولین علامت \(\مثلث ABD=\مثلث ACD\) (\(AC=BD، \زاویه OAD=\زاویه ODA، AD\)- عمومی). بنابراین، \(AB=CD\) چرا.

ذوزنقه حالت خاصی از چهار ضلعی است که در آن یک جفت ضلع موازی است. اصطلاح "ذوزنقه" از کلمه یونانی τράπεζα به معنای "میز"، "میز" گرفته شده است. در این مقاله به بررسی انواع ذوزنقه و خواص آن می پردازیم. علاوه بر این، نحوه محاسبه عناصر منفرد این را خواهیم فهمید، به عنوان مثال، مورب ذوزنقه متساوی الساقین، خط مرکزی، مساحت و غیره. .

اطلاعات عمومی

ابتدا بیایید بفهمیم که چهارضلعی چیست. این شکل یک حالت خاص از یک چند ضلعی است که شامل چهار ضلع و چهار راس است. دو رأس یک چهار ضلعی که مجاور هم نباشند مخالف نامیده می شوند. همین را می توان برای دو ضلع غیر مجاور نیز گفت. انواع اصلی چهارضلعی ها متوازی الاضلاع، مستطیل، لوزی، مربع، ذوزنقه و دلتوئید هستند.

پس بیایید به ذوزنقه ها برگردیم. همانطور که قبلاً گفتیم این رقم دارای دو ضلع موازی است. به آنها پایگاه می گویند. دو طرف دیگر (غیر موازی) اضلاع جانبی هستند. در مواد امتحانات و تست های مختلف اغلب می توانید مشکلات مربوط به ذوزنقه ها را بیابید که حل آنها اغلب مستلزم داشتن دانشی است که در برنامه پیش بینی نشده است. درس هندسه مدرسه دانش آموزان را با ویژگی های زاویه ها و مورب ها و همچنین خط وسط ذوزنقه متساوی الساقین آشنا می کند. اما علاوه بر این، شکل هندسی مذکور ویژگی های دیگری نیز دارد. اما در مورد آنها کمی بعد ...

انواع ذوزنقه

انواع مختلفی از این شکل وجود دارد. با این حال، اغلب مرسوم است که دو مورد از آنها را در نظر بگیریم - متساوی الساقین و مستطیل.

1. ذوزنقه مستطیلی شکلی است که یکی از اضلاع آن بر پایه ها عمود باشد. دو زاویه او همیشه برابر با نود درجه است.

2. ذوزنقه متساوی الساقین شکل هندسی است که اضلاع آن با یکدیگر برابر است. این بدان معنی است که زوایای پایه ها نیز به صورت جفت برابر هستند.

اصول اصلی روش شناسی برای مطالعه خواص ذوزنقه

اصل اصلی شامل استفاده از رویکرد به اصطلاح وظیفه است. در واقع نیازی به وارد کردن ویژگی های جدید این شکل در درس هندسه نظری نیست. آنها را می توان در فرآیند حل مسائل مختلف (ترجیحاً سیستمی) کشف و فرموله کرد. در عین حال، بسیار مهم است که معلم بداند چه وظایفی باید در یک دوره آموزشی به دانش آموزان محول شود. علاوه بر این، هر ویژگی ذوزنقه می تواند به عنوان یک وظیفه کلیدی در سیستم وظیفه نمایش داده شود.

اصل دوم، سازماندهی به اصطلاح مارپیچی برای مطالعه خواص "قابل توجه" ذوزنقه است. این به معنای بازگشت در فرآیند یادگیری به ویژگی های فردی یک شکل هندسی معین است. این باعث می شود دانش آموزان راحت تر آنها را به خاطر بسپارند. مثلاً خاصیت چهار نقطه. هم هنگام مطالعه شباهت و هم پس از آن با استفاده از بردارها می توان آن را ثابت کرد. و هم ارزی مثلث های مجاور اضلاع یک شکل را می توان نه تنها با اعمال خواص مثلث هایی با ارتفاع مساوی که به ضلع هایی که روی یک خط مستقیم قرار دارند، بلکه با استفاده از فرمول S = 1/2 نیز اثبات کرد. ab*sina). علاوه بر این، می توانید بر روی ذوزنقه حکاکی شده یا مثلث قائم الزاویه روی ذوزنقه حکاکی شده و غیره کار کنید.

استفاده از ویژگی های "خارج از برنامه" یک شکل هندسی در محتوای یک دوره مدرسه یک فناوری مبتنی بر وظیفه برای آموزش آنها است. مراجعه مداوم به ویژگی های مورد مطالعه در حین مرور موضوعات دیگر به دانش آموزان امکان می دهد تا دانش عمیق تری از ذوزنقه به دست آورند و موفقیت در حل مسائل تعیین شده را تضمین می کند. بنابراین، بیایید شروع به مطالعه این شکل شگفت انگیز کنیم.

عناصر و خواص ذوزنقه متساوی الساقین

همانطور که قبلاً اشاره کردیم، این شکل هندسی دارای اضلاع مساوی است. به ذوزنقه صحیح نیز معروف است. چرا اینقدر قابل توجه است و چرا چنین نامی به خود گرفته است؟ ویژگی این شکل این است که نه تنها اضلاع و زوایای پایه ها، بلکه مورب ها نیز برابر هستند. به علاوه مجموع زوایای ذوزنقه متساوی الساقین 360 درجه است. اما این همه ماجرا نیست! از میان همه ذوزنقه‌های شناخته شده، فقط یک متساوی الساقین را می‌توان به عنوان دایره توصیف کرد. این به این دلیل است که مجموع زوایای مقابل این شکل برابر با 180 درجه است و فقط در این شرایط می توان دایره ای را در اطراف یک چهار ضلعی توصیف کرد. خاصیت بعدی شکل هندسی مورد بررسی این است که فاصله راس قاعده تا برآمدگی راس مقابل بر روی خط مستقیمی که این قاعده را در خود دارد برابر با خط وسط خواهد بود.

حالا بیایید بفهمیم که چگونه زوایای یک ذوزنقه متساوی الساقین را پیدا کنیم. اجازه دهید راه حلی برای این مشکل در نظر بگیریم، مشروط بر اینکه ابعاد اضلاع شکل مشخص باشد.

راه حل

به طور معمول، چهار ضلعی معمولا با حروف A، B، C، D نشان داده می شود، که در آن BS و AD پایه هستند. در ذوزنقه متساوی الساقین، اضلاع با هم برابر هستند. اندازه آنها را برابر با X و اندازه پایه ها را برابر با Y و Z (به ترتیب کوچکتر و بزرگتر) فرض خواهیم کرد. برای انجام محاسبات، لازم است که ارتفاع H را از زاویه B رسم کنیم. نتیجه یک مثلث قائم الزاویه ABN است که AB هیپوتانوس و BN و AN پاها هستند. اندازه ساق AN را محاسبه می کنیم: پایه کوچکتر را از پایه بزرگتر کم می کنیم و حاصل را بر 2 تقسیم می کنیم. آن را به صورت فرمول می نویسیم: (Z-Y)/2 = F. حالا برای محاسبه حاد زاویه مثلث، از تابع cos استفاده می کنیم. ورودی زیر را دریافت می کنیم: cos(β) = X/F. حالا زاویه را محاسبه می کنیم: β=arcos (X/F). علاوه بر این، با دانستن یک زاویه، می توانیم دومی را تعیین کنیم، برای این کار یک عملیات حسابی ابتدایی را انجام می دهیم: 180 - β. همه زوایا تعریف شده است.

راه حل دومی برای این مشکل وجود دارد. ابتدا آن را از گوشه به ارتفاع H پایین می آوریم. مقدار پایه BN را محاسبه می کنیم. می دانیم که مجذور هیپوتنوز مثلث قائم الزاویه برابر است با مجموع مربع های پاها. دریافت می کنیم: BN = √(X2-F2). سپس از تابع مثلثاتی tg استفاده می کنیم. در نتیجه داریم: β = آرکتان (BN/F). یک زاویه حاد پیدا شده است. در مرحله بعد، آن را مشابه روش اول تعریف می کنیم.

ویژگی قطرهای ذوزنقه متساوی الساقین

ابتدا اجازه دهید چهار قانون را بنویسیم. اگر قطرهای ذوزنقه متساوی الساقین عمود بر هم باشند، آنگاه:

ارتفاع شکل برابر با مجموع پایه ها تقسیم بر دو خواهد بود.

ارتفاع و خط وسط آن برابر است.

مرکز دایره نقطه ای است که در آن ;

اگر ضلع جانبی توسط نقطه مماس به قطعات H و M تقسیم شود، آنگاه برابر است با جذر حاصلضرب این قطعات.

چهارضلعی که از نقاط مماس، راس ذوزنقه و مرکز دایره محاطی تشکیل می شود، مربعی است که ضلع آن برابر با شعاع است.

مساحت یک شکل برابر است با حاصل ضرب پایه ها و حاصل ضرب نصف مجموع پایه ها و ارتفاع آن.

ذوزنقه های مشابه

این مبحث برای مطالعه خواص این بسیار مناسب است، به عنوان مثال، مورب ها یک ذوزنقه را به چهار مثلث تقسیم می کنند و آنهایی که در مجاورت پایه ها قرار دارند مشابه هستند و آنهایی که مجاور اضلاع هستند از نظر اندازه برابر هستند. این عبارت را می توان ویژگی مثلث هایی نامید که ذوزنقه بر اساس قطرهایش به آنها تقسیم می شود. قسمت اول این گفته از طریق علامت تشابه در دو زاویه ثابت می شود. برای اثبات قسمت دوم بهتر است از روش زیر استفاده کنید.

اثبات قضیه

می پذیریم که شکل ABSD (AD و BS پایه های ذوزنقه هستند) به قطرهای VD و AC تقسیم شده است. نقطه تقاطع آنها O است. ما چهار مثلث داریم: AOS - در پایه پایین، BOS - در پایه بالا، ABO و SOD در اضلاع. مثلث های SOD و BOS دارای ارتفاع مشترک هستند اگر قطعات BO و OD پایه آنها باشند. ما متوجه شدیم که تفاوت بین مساحت آنها (P) برابر است با تفاوت بین این بخش ها: PBOS/PSOD = BO/OD = K. بنابراین، PSOD = PBOS/K. به طور مشابه، مثلث های BOS و AOB دارای ارتفاع مشترک هستند. ما بخش های CO و OA را به عنوان پایه آنها در نظر می گیریم. ما PBOS/PAOB = CO/OA = K و PAOB = PBOS/K را دریافت می کنیم. از این نتیجه می شود که PSOD = PAOB.

برای تجمیع مطالب، به دانش‌آموزان توصیه می‌شود تا با حل مسئله زیر، ارتباط بین مناطق مثلث‌های حاصل را که ذوزنقه بر اساس قطرهای آن تقسیم می‌شود، بیابند. مشخص است که مثلث های BOS و AOD دارای مساحت مساوی هستند. از آنجایی که PSOD = PAOB، به معنای PABSD = PBOS + PAOD + 2 * PSOD است. از شباهت مثلث های BOS و AOD نتیجه می شود که BO/OD = √(PBOS/PAOD). بنابراین PBOS/PSOD = BO/OD = √(PBOS/PAOD). ما PSOD = √ (PBOS*PAOD) را دریافت می کنیم. سپس PABSD = PBOS+PAOD+2*√(PBOS*PAOD) = (√PBOS+√PAOD)2.

خواص تشابه

با ادامه توسعه این موضوع، می‌توانیم ویژگی‌های جالب دیگر ذوزنقه‌ها را ثابت کنیم. بنابراین با استفاده از تشابه می توان خاصیت پاره ای را که از نقطه ای که از تقاطع مورب های این شکل هندسی به موازات قاعده ها تشکیل شده است را اثبات کرد. برای انجام این کار، اجازه دهید مشکل زیر را حل کنیم: باید طول قطعه RK را که از نقطه O عبور می کند، پیدا کنیم. از شباهت مثلث های AOD و BOS نتیجه می شود که AO/OS = AD/BS. از شباهت مثلث های AOP و ASB چنین بر می آید که AO/AC=RO/BS=AD/(BS+AD). از اینجا دریافت می کنیم که RO=BS*BP/(BS+BP). به همین ترتیب، از تشابه مثلث های DOC و DBS، نتیجه می شود که OK = BS*AD/(BS+AD). از اینجا دریافت می کنیم که RO=OK و RK=2*BS*AD/(BS+AD). قطعه ای که از نقطه تقاطع مورب ها به موازات پایه ها می گذرد و دو ضلع جانبی را به هم وصل می کند، توسط نقطه تقاطع به نصف تقسیم می شود. طول آن میانگین هارمونیک پایه های شکل است.

ویژگی زیر ذوزنقه را در نظر بگیرید که به آن خاصیت چهار نقطه می گویند. نقاط تقاطع مورب ها (O)، محل تلاقی ادامه اضلاع (E) و همچنین نقاط میانی پایه ها (T و F) همیشه روی یک خط قرار دارند. این را می توان به راحتی با روش تشابه اثبات کرد. مثلث های BES و AED به دست آمده مشابه هستند و در هر یک از آنها میانه های ET و EJ زاویه رأس E را به قسمت های مساوی تقسیم می کنند. بنابراین، نقاط E، T و F روی یک خط مستقیم قرار دارند. به همین ترتیب، نقاط T، O، و Zh در یک خط مستقیم قرار دارند. از اینجا نتیجه می گیریم که هر چهار نقطه - E، T، O و F - روی یک خط مستقیم قرار می گیرند.

با استفاده از ذوزنقه های مشابه، می توانید از دانش آموزان بخواهید طول قطعه (LF) را که شکل را به دو قسمت مشابه تقسیم می کند، بیابند. این قطعه باید موازی با پایه ها باشد. از آنجایی که ذوزنقه های حاصل ALFD و LBSF مشابه هستند، پس BS/LF = LF/AD. نتیجه این است که LF=√(BS*AD). متوجه شدیم که قطعه ای که ذوزنقه را به دو قسمت مشابه تقسیم می کند، طولی برابر با میانگین هندسی طول پایه های شکل دارد.

ویژگی تشابه زیر را در نظر بگیرید. بر اساس قطعه ای است که ذوزنقه را به دو شکل مساوی تقسیم می کند. ما فرض می کنیم که ABSD ذوزنقه ای توسط قطعه EH به دو قطعه مشابه تقسیم می شود. از راس B یک ارتفاع حذف شده است که توسط بخش EN به دو قسمت - B1 و B2 تقسیم می شود. دریافت می کنیم: PABSD/2 = (BS+EN)*B1/2 = (AD+EN)*B2/2 و PABSD = (BS+AD)*(B1+B2)/2. سپس، سیستمی را می سازیم که اولین معادله آن (BS+EN)*B1 = (AD+EN)*B2 و معادله دوم (BS+EN)*B1 = (BS+AD)*(B1+B2)/2 باشد. نتیجه می شود که B2/B1 = (BS+EN)/(AD+EN) و BS+EN = ((BS+AD)/2)*(1+B2/B1). متوجه می‌شویم که طول قطعه‌ای که ذوزنقه را به دو قسمت مساوی تقسیم می‌کند برابر است با ریشه میانگین مربع طول پایه‌ها: √((BS2+AD2)/2).

یافته های شباهت

بنابراین، ما ثابت کردیم که:

1. پاره ای که نقاط میانی اضلاع ذوزنقه را به هم وصل می کند، موازی با AD و BS است و برابر است با میانگین حسابی BS و AD (طول قاعده ذوزنقه).

2. خطی که از نقطه O تقاطع قطرهای موازی AD و BS می گذرد برابر با میانگین هارمونیک اعداد AD و BS (2*BS*AD/(BS+AD)) خواهد بود.

3. پاره ای که ذوزنقه را به قطعات مشابه تقسیم می کند، طول میانگین هندسی پایه های BS و AD را دارد.

4. عنصری که یک شکل را به دو عدد مساوی تقسیم می کند دارای طول ریشه مجذور میانگین اعداد AD و BS است.

برای ادغام مطالب و درک ارتباط بین بخش های در نظر گرفته شده، دانش آموز باید آنها را برای یک ذوزنقه خاص بسازد. او به راحتی می تواند خط وسط و قطعه ای را که از نقطه O - محل تقاطع مورب های شکل - موازی با پایه ها عبور می کند، نمایش دهد. اما سومین و چهارمین کجا قرار خواهند گرفت؟ این پاسخ دانش آموز را به کشف رابطه مطلوب بین مقادیر متوسط ​​می رساند.

پاره ای که نقاط میانی قطرهای ذوزنقه را به هم وصل می کند

ویژگی زیر را در این شکل در نظر بگیرید. فرض می کنیم که قطعه MH موازی با قاعده ها است و قطرها را نصف می کند. نقطه های تقاطع Ш و Ш را می نامیم. بیایید به این موضوع با جزئیات بیشتری نگاه کنیم. MS خط وسط مثلث ABS است که برابر با BS/2 است. MSH خط وسط مثلث ABD است که برابر با AD/2 است. سپس دریافت می کنیم که ShShch = MSh-Msh، بنابراین، ShShch = AD/2-BS/2 = (AD+VS)/2.

مرکز ثقل

بیایید ببینیم که چگونه این عنصر برای یک شکل هندسی مشخص تعیین می شود. برای انجام این کار، لازم است که پایه ها را در جهت مخالف گسترش دهید. به چه معناست؟ شما باید پایه پایین را به پایه بالایی اضافه کنید - در هر جهت، به عنوان مثال، به سمت راست. و قسمت پایینی را به طول قسمت بالایی به سمت چپ گسترش می دهیم. سپس آنها را به صورت مورب به هم وصل می کنیم. نقطه تلاقی این قطعه با خط وسط شکل مرکز ثقل ذوزنقه است.

ذوزنقه های کتیبه دار و محصور

بیایید ویژگی های چنین ارقامی را فهرست کنیم:

1. ذوزنقه را فقط در صورتی می توان به صورت دایره ای حک کرد که متساوی الساقین باشد.

2. ذوزنقه را می توان حول دایره توصیف کرد، مشروط بر اینکه مجموع طول پایه های آنها با مجموع طول اضلاع برابر باشد.

پیامدهای دایره:

1. ارتفاع ذوزنقه توصیف شده همیشه برابر با دو شعاع است.

2. ضلع ذوزنقه توصیف شده از مرکز دایره با زاویه قائمه مشاهده می شود.

نتیجه اول واضح است، اما برای اثبات دومی باید ثابت کرد که زاویه SOD درست است، که در واقع دشوار نیست. اما آگاهی از این ویژگی به شما این امکان را می دهد که در حل مسائل از مثلث قائم الزاویه استفاده کنید.

حال اجازه دهید این پیامدها را برای ذوزنقه متساوی الساقین که در یک دایره حک شده است مشخص کنیم. متوجه می شویم که ارتفاع، میانگین هندسی پایه های شکل است: H=2R=√(BS*AD). دانش آموز در حین تمرین تکنیک اساسی برای حل مسائل ذوزنقه ای (اصل ترسیم دو ارتفاع) باید تکلیف زیر را حل کند. فرض می کنیم که BT ارتفاع شکل متساوی الساقین ABSD است. یافتن بخش های AT و TD ضروری است. با استفاده از فرمول شرح داده شده در بالا، انجام این کار دشوار نخواهد بود.

حالا بیایید بفهمیم که چگونه شعاع دایره را با استفاده از مساحت ذوزنقه محدود تعیین کنیم. ارتفاع را از راس B به پایه AD کم می کنیم. از آنجایی که دایره در یک ذوزنقه حک شده است، پس BS+AD = 2AB یا AB = (BS+AD)/2. از مثلث ABN، sinα = BN/AB = 2*BN/(BS+AD) را پیدا می کنیم. PABSD = (BS+BP)*BN/2، BN=2R. ما PABSD = (BS+BP)*R را دریافت می کنیم، نتیجه آن این است که R = PABSD/(BS+BP).

تمام فرمول های خط وسط ذوزنقه

حالا وقت آن است که به آخرین عنصر این شکل هندسی برویم. بیایید بفهمیم که خط وسط ذوزنقه (M) برابر است با:

1. از طریق پایه ها: M = (A+B)/2.

2. از طریق ارتفاع، پایه و گوشه ها:

M = A-H*(ctgα+ctgβ)/2;

M = B+N*(ctgα+ctgβ)/2.

3. از طریق ارتفاع، مورب و زاویه بین آنها. برای مثال، D1 و D2 قطرهای ذوزنقه هستند. α، β - زوایای بین آنها:

M = D1*D2*sinα/2N = D1*D2*sinβ/2N.

4. از طریق مساحت و ارتفاع: M = P/N.