Модуль векторного произведения векторов формула. Векторное произведение векторов, определение, свойства

Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,

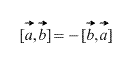
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:

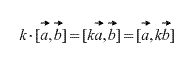
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).

Векторное произведение обладает распределительным свойством , то есть

Выражение векторного произведения через координаты векторов.

Пусть даны два вектора

(как найти координаты вектора по координатам его начала и конца - см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )

Зачем нужно векторное произведение?

Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.

Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.

Также огромное количество применений существует в электричестве и магнетизме.

Он-лайн калькулятор векторного произведения.

Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )

7.1. Определение векторного произведения

Три некомпланарных вектора a , b и с , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

Векторным произведением вектора а на вектор b называется вектор с , который:

1. Перпендикулярен векторам a и b , т. е. с ^ а и с ^ b ;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3. Векторы a , b и с образуют правую тройку.

Векторное произведение обозначается а х b или [а ,b ]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k , j х k = i , k х i = j .
Докажем, например, что i хj =k .

1) k ^ i , k ^ j ;

2) |k |=1, но | i x j | = |i | |J | sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

7.2. Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).

Векторы а хb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , b x a противоположной ориентации). Стало быть a xb = -(b xa ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l (а хb ) = (l а ) х b = а х (l b ).

Пусть l >0. Вектор l (а хb ) перпендикулярен векторам а и b . Вектор ( l а )хb также перпендикулярен векторам а и b (векторы а , l а лежат в одной плоскости). Значит, векторы l (а хb ) и ( l а )хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому l (a хb )= l а хb . Аналогично доказывается при l <0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а ||b <=>а хb =0 .

В частности, i *i =j *j =k *k =0 .

4. Векторное произведение обладает распределительным свойством:

(a +b ) хс = а хс +b хс .

Примем без доказательства.

7.3. Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов i , j и k :

если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает - третий вектор берется со знаком «минус».

Пусть заданы два вектора а =а х i +a y j +a z k и b =b x i +b y j +b z k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

Полученную формулу можно записать еще короче:

так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки.Равенство (7.2) легко запоминается.

7.4. Некоторые приложения векторного произведения

Установление коллинеарности векторов

Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов а и b |а хb | = |а | * |b |sin g , т. е. S пар = |а х b |. И, значит, D S =1/2|а х b |.

Определение момента силы относительно точки

Пусть в точке А приложена сила F =АВ и пусть О - некоторая точка пространства (см. рис. 20).

Из физики известно, что моментом си лы F относительно точки О называется вектор М , который проходит через точку О и:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2) численно равен произведению силы на плечо

3) образует правую тройку с векторами ОА и A В .

Стало быть, М =ОА х F .

Нахождение линейной скорости вращения

Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ , где О-некоторая неподвижная точка оси (см. рис. 21).

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ И ЕГО СВОЙСТВА

Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .
Таким образом, и .

Доказательство . Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что . По определению скалярного произведения

Предполагая, что и обозначив через h высоту параллелепипеда, находим .

Таким образом, при

Если же , то и . Следовательно, .

Объединяя оба эти случая, получаем или .

Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .
Для любых векторов , , справедливо равенство
Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами и и и одновременно острые или тупые.
При перестановке любых двух сомножителей смешанное произведение меняет знак.
Действительно, если рассмотрим смешанное произведение , то, например, или
Смешанное произведение тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.
Доказательство .

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

.

Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Примеры.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Уравнение F(x, y, z) = 0 определяет в пространстве Oxyz некоторую поверхность, т.е. геометрическое место точек, координаты которых x, y, z удовлетворяют этому уравнению. Это уравнение называется уравнением поверхности, а x, y, z – текущими координатами.

Однако, часто поверхность задаётся не уравнением, а как множество точек пространства, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из её геометрических свойств.

ПЛОСКОСТЬ.

НОРМАЛЬНЫЙ ВЕКТОР ПЛОСКОСТИ.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M 0 (x 0 , y 0 , z 0 ), лежащей в плоскости σ.

Вектор перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор имеет координаты .

Выведем уравнение плоскости σ, проходящей через данную точку M 0 и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки M Î σ вектор .Поэтому их скалярное произведение равно нулю . Это равенство – условие того, что точка M Î σ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через радиус-вектор точки M , – радиус-вектор точкиM 0 , то и уравнение можно записать в виде

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как , то

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z .

Примеры.

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:

Ax+By+Cz+D =0

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

A – это длина отрезка, отсекаемого плоскостью на оси Ox . Аналогично, можно показать, что b и c – длины отрезков, отсекаемых рассматриваемой плоскостью на осях Oy и Oz .

Уравнением плоскости в отрезках удобно пользоваться для построения плоскостей.

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.

Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой , если по часовой стрелке – левой .

Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Определение 1

Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы a → и b → коллинеарны, он будет нулевым;
он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) называют вектор c → = a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k → , где i → , j → , k → являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k →

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

антикоммутативность a → × b → = - b → × a → ;
дистрибутивность a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
ассоциативность λ · a → × b → = λ · a → × b → или a → × (λ · b →) = λ · a → × b → , где λ - произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .

Пример 1

Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

Решение

С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Ответ: 15 2 2 .

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) .

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Ответ: a → × b → = - 2 i → - 2 j → - 2 k → .

Пример 3

Найдите длину векторного произведения векторов i → - j → и i → + j → + k → , где i → , j → , k → - орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i → - j → × i → + j → + k → в данной прямоугольной системе координат.

Известно, что векторы i → - j → и i → + j → + k → имеют координаты (1 ; - 1 ; 0) и (1 ; 1 ; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Следовательно, векторное произведение i → - j → × i → + j → + k → имеет координаты (- 1 ; - 1 ; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Ответ: i → - j → × i → + j → + k → = 6 . .

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A (1 , 0 , 1) , B (0 , 2 , 3) , C (1 , 4 , 2) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.

Решение

Векторы A B → и A C → имеют следующие координаты (- 1 ; 2 ; 2) и (0 ; 4 ; 1) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи. Найдем его A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Ответ: - 6 i → + j → - 4 k → . - один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b →

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b →

Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Из антикоммутативности векторного произведения следует - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → - b → × a → - 2 · b → = - 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Ответ: 3 · a → - b → × a → - 2 · b → = 60 .

Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма - удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Определение 3

Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Определение. Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [«, Ь] (или л х Ь), такой, что 1) длина вектора [а, b] равна (р, где у - угол между векторами а и b (рис.31); 2) вектор [а, Ь) перпендикулярен векторам а и Ь,т.е. перпендикулярен плоскости этих векторов; 3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от а к b виден происходящим против часовой стрелки (рис. 32). Рис. 32 Рис.31 Иными словами, векторы a, b и [а,Ь) образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы а и b коллинеарны, будем считать, что [а, Ь] = 0. По определению длина векторного произведения численно равна площади Sa параллелограмма (рис. 33), построенного на перемножаемых векторах а и b как на сторонах: 6.1. Свойства векторного произведения 1. Векторное произведение равно нулевому вектору тогда и толькотогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы а и b коллинеарны, то угол между ними равен либо 0, либо 7г). Это легко получить из того, что Если считать нулевой вектор коллинсарным любому вектору, то условие коллинеарности векторов а и b можно выразить так 2. Векторное произведение антикоммутативно, т. е. всегда. В самом деле, векторы (а, Ь) и имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [а, Ь] кратчайший поворот от а к b будет виден происходящим против часовой стрелки, а из конца вектора [Ь, а] - по часовой стрелке (рис. 34). 3. Векторное произведение обладает распределительным свойством по отношению к сложению 4. Числовой множитель Л можно выносить за знак векторного произведения 6.2. Векторное произведение векторов, заданных координатами Пусть векторы а и Ь заданы своими координатами в базисе. Пользуясь распределительным свойством векторного произведения, находим Векторное произведение векторов заданных координатами. Смешанное произведение. Выпишем векторные произведения координатных ортов (рис. 35): Поэтому для векторного произведения векторов а и b получаем из формулы (3) следующее выражение Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры. 1. Найти площадь параллелограмма, построенного на векторах Искомая площадь Поэтому находим = откуда 2. Найти площадь треугольника (рис. 36). Ясно, что площадь б"д треугольника ОАО равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение (а, Ь| векторов а = OA и b = оЪ, получаем Отсюда Замечание. Векторное произведение не ассоциативно, т.е. равенство ((а, Ь),с) = [а, |Ь,с)) в обшем случае неверно. Например, при а = ss j имеем § 7. Смешанное произведение векторов Пусть имеем три вектора а, Ь и с. Перемножим векторы а и 1> вскторно. В результате получим вектор [а, 1>]. Умножим его скалярно на вектор с: (к Ь), с). Число ([а, Ь], е) называется смешанным произведением векторов а, Ь. с и обозначается символом (а, 1), е). 7.1. Геометрический смысл смешанного произведения Отложим векторы а, b и с отобшей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, Ь], с) = 0. Это следует из того, что вектор [а, Ь| перпендикулярен плоскости, в которой лежат векторы а и 1», а значит, и вектору с. / Если же точки О, А, В, С не лежат в одной плос-кости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем (a,b) = So с, где So - площадь параллелограмма OADB, а с - единичный вектор, перпендикулярный векторам а и Ь и такой, что тройка а, Ь, с - правая, т.е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 б). Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что Векторное произведение векторов заданных координатами. Смешанное произведение. Число ргс с равно высоте h построенного параллелепипеда, взятого со знаком «+», если угол между векторами с и с острый (тройка а, Ь, с - правая), и со знаком «-», если угол - тупой (тройка а, Ь, с - левая), так что Тем самым, смешанное произведение векторов а, Ь и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, Ъ, с - правая, и -V, если тройка а, Ь, с - левая. Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая тс же векторы a, b и с в любом другом порядке, мы всегда будем получать либо +7, либо -К. Знак произ- Рис. 38 ведения будет зависеть лишь оттого, какую тройку образуют перемножаемые векторы - правую или левую. Если векторы а, Ь, с образуют правую тройку, то правыми будут также тройки Ь, с, а и с, а, Ь. В то же время все три тройки Ь, а, с; а, с, Ь и с, Ь, а - левые. Тем самым, (а,Ь, с) = (Ь,с, а) = (с,а,Ь) = -(Ь,а,с) = -(а,с,Ь) = -(с,Ь,а). Ешераз подчеркнем, что смешанное произведение векторов равно нулютогдаи только тогда, когда перемножаемые векторы а, Ь, с компланарны: {а, Ь, с компланарны} 7.2. Смешанное произведение в координатах Пусть векторы а, Ь, с заданы своими координатами в базисе i, j, k: а = {x\,y\,z]}, b= {x2,y2>z2}, c = {х3,уз,23}. Найдем выражение для их смешанного произведения (а, Ь, с). Имеем смешанное произведение векторов, заданныхсвоими координатами в базисе i, J, к, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов. Необходимое и достаточное условие компланарности векторов а у\, Z|}, b = {хъ У2. 22}, с = {жз, уз, 23} запишется в следующем виде У| z, аг2 у2 -2 =0. Уз Пример. Проверить, компланарны ли векторы „ = {7,4,6}, Ь = {2, 1,1}, с = {19, II, 17}. Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель Разлагая его по элементам первой строки, получим Д = 7- 6- 4- 15 + 6-3 = 0^- векторы n, Ь, с компланарны. 7.3. Двойное векторное произведение Двойное векторное произведение [а, [Ь, с]] представляет собой вектор, перпендикулярный к векторам а и [Ь, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула [а, [!>, с]] = Ь(а, е) - с(а, Ъ). Упражнения 1. Три вектора АВ = с, Ж? = о и СА = b служат сторонами треугольника. Выразить через a, b и с векторы, совпадающие с медианами AM, DN, CP треугольника. 2. Каким условием должны быть связаны векторы р и q, чтобы вектор р + q делил угол между ними пополам? Предполагается, что все три вектора отнесены к общему началу. 3. Вычислите длину диагоналей параллелограмма, построенного на векторах а = 5р + 2q и b = р - 3q, если известно, что |р| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Обозначив через а и b стороны ромба, выходящие из общей вершины, докажите, что диагонали ромба взаимно перпендикулярны. 5. Вычислите скалярное произведение векторов а = 4i + 7j + 3k и b = 31 - 5j + k. 6. Найдите единичный вектор а0, параллельный вектору а = {6, 7, -6}. 7. Найдите проекцию вектора a = l+ j- kHa вектор b = 21 - j - 3k. 8. Найдите косинус угла между векторами IS «ж,если А(-4,0,4), В(-1,6,7), С(1,10.9). 9. Найдите единичный вектор р°, одновременно перпендикулярный вектору а = {3, 6, 8} и оси Ох. 10. Вычислите синус угла между диагоналями параллелофамма, построенного на векторах a = 2i+J-k, b=i-3j + k как на сторонах. Вычислите высоту h параллелепипеда, построенного на векторах а = 31 + 2j - 5k, b = i- j + 4knc = i-3j + к, если за основание взят параллелограмм, построенный на векторах а и I). Ответы