Príklady exponenciálnych funkcií. Exponenciálne rovnice a nerovnice
Hypermarket vedomostí >>Matematika >>Matematika 10. ročník >>
Exponenciálna funkcia, jej vlastnosti a graf
Uvažujme výraz 2x a nájdime jeho hodnoty pre rôzne racionálne hodnoty premennej x, napríklad pre x = 2;
Vo všeobecnosti platí, že bez ohľadu na to, aký racionálny význam priradíme premennej x, vždy vieme vypočítať zodpovedajúcu číselnú hodnotu výrazu 2 x. Môžeme teda hovoriť o exponenciálnom funkcie y=2 x, definované na množine Q racionálnych čísel:
Pozrime sa na niektoré vlastnosti tejto funkcie.
Nehnuteľnosť 1.- zvýšenie funkcie. Dôkaz vykonávame v dvoch etapách.
Prvá etapa. Dokážme, že ak r je kladné racionálne číslo, potom 2 r >1.
Možné sú dva prípady: 1) r je prirodzené číslo, r = n; 2) obyčajný neredukovateľný zlomok,
Na ľavej strane poslednej nerovnosti máme , a na pravej strane 1. To znamená, že poslednú nerovnosť je možné prepísať do tvaru
Takže v každom prípade platí nerovnosť 2 r > 1, čo bolo potrebné dokázať.
Druhá etapa. Nech x 1 a x 2 sú čísla a x 1 a x 2< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования:
(rozdiel x 2 - x 1 sme označovali písmenom r).
Keďže r je kladné racionálne číslo, potom podľa toho, čo bolo dokázané v prvej fáze, 2 r > 1, t.j. 2r-1 >0. Číslo 2x" je tiež kladné, čo znamená, že súčin 2 x-1 (2 Г -1) je tiež kladný. Dokázali sme teda, že nerovnosť 2 Xg -2x" >0.
Takže z nerovnosti x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая.
Nehnuteľnosť 2. obmedzené zdola a neobmedzené zhora.
Ohraničenosť funkcie zdola vyplýva z nerovnosti 2 x > 0, ktorá platí pre ľubovoľné hodnoty x z oblasti definície funkcie. Zároveň bez ohľadu na to, aké kladné číslo M vezmete, vždy môžete zvoliť exponent x taký, aby bola splnená nerovnosť 2 x >M – čo charakterizuje neohraničenosť funkcie zhora. Uveďme niekoľko príkladov.
Nehnuteľnosť 3. nemá ani najmenšiu, ani najväčšiu hodnotu.
To, že táto funkcia nemá najväčší význam, je zrejmé, pretože, ako sme práve videli, nie je ohraničená vyššie. Ale je to obmedzené zdola, prečo to nemá minimálnu hodnotu?
Predpokladajme, že 2 r je najmenšia hodnota funkcie (r je nejaký racionálny ukazovateľ). Zoberme si racionálne číslo q<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции.
To všetko je dobré, hovoríte, ale prečo funkciu y-2 x uvažujeme len na množine racionálnych čísel, prečo ju neuvažujeme ako iné známe funkcie na celej číselnej osi alebo na nejakom súvislom intervale číselný rad? Čo nám v tom bráni? Zamyslime sa nad situáciou.
Číselný rad obsahuje nielen racionálne, ale aj iracionálne čísla. Pri predtým študovaných funkciách nám to neprekážalo. Napríklad hodnoty funkcie y = x2 sme našli rovnako ľahko pre racionálne aj iracionálne hodnoty x: stačilo odmocniť danú hodnotu x.
Ale s funkciou y=2 x je situácia zložitejšia. Ak má argument x racionálny význam, potom možno v princípe x vypočítať (vráťte sa opäť na začiatok odseku, kde sme presne toto urobili). Čo ak má argument x iracionálny význam? Ako napríklad vypočítať? Toto ešte nevieme.
Matematici našli cestu von; takto uvažovali.
To je známe 
Zvážte postupnosť racionálnych čísel - desiatkové aproximácie čísla nevýhodou:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .
Je jasné, že 1,732 = 1,7320 a 1,732050 = 1,73205. Aby sme sa vyhli takýmto opakovaniam, vyradíme tie členy postupnosti, ktoré končia číslom 0.
Potom dostaneme rastúcu postupnosť:
1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .
V súlade s tým sa postupnosť zvyšuje
Všetky členy tejto postupnosti sú kladné čísla menšie ako 22, t.j. táto postupnosť je obmedzená. Podľa Weierstrassovej vety (pozri § 30) ak je postupnosť rastúca a ohraničená, potom konverguje. Okrem toho z § 30 vieme, že ak postupnosť konverguje, tak len do jednej limity. Bolo dohodnuté, že tento jediný limit by sa mal považovať za hodnotu číselného vyjadrenia. A nezáleží na tom, že je veľmi ťažké nájsť čo i len približnú hodnotu číselného výrazu 2; dôležité je, že ide o konkrétne číslo (napokon, nebáli sme sa povedať, že je to napríklad koreň racionálnej rovnice, 
koreň trigonometrickej rovnice, bez toho, aby sme skutočne premýšľali o tom, čo presne sú tieto čísla: 
Zistili sme teda, aký význam vkladajú matematici do symbolu 2^. Podobne môžete určiť, čo a vo všeobecnosti čo je a a, kde a je iracionálne číslo a a > 1.
Ale čo ak 0<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
Teraz môžeme hovoriť nielen o mocniciach s ľubovoľnými racionálnymi exponentmi, ale aj o mocninách s ľubovoľnými skutočnými exponentmi. Je dokázané, že stupne s akýmikoľvek reálnymi exponentmi majú všetky obvyklé vlastnosti stupňov: pri násobení mocnín s rovnakými základmi sa exponenty sčítajú, pri delení sa odčítajú, pri zvýšení stupňa na mocninu sa násobia atď. Najdôležitejšie však je, že teraz môžeme hovoriť o funkcii y-ax definovanej na množine všetkých reálnych čísel.
Vráťme sa k funkcii y = 2 x a zostavme jej graf. Aby sme to dosiahli, vytvorte tabuľku funkčných hodnôt y=2x:
Označme body na súradnicovej rovine (obr. 194), vyznačujú určitú čiaru, narysujme ju (obr. 195).
Vlastnosti funkcie y - 2 x:
1)
2) nie je párne ani nepárne; 248
3) zvyšuje;
5) nemá najväčšie ani najmenšie hodnoty;
6) kontinuálne;
7)
8) konvexné smerom nadol.
Dôkladné dôkazy uvedených vlastností funkcie y-2 x sú uvedené v kurze vyššej matematiky. Niektoré z týchto vlastností sme do istej miery diskutovali skôr, niektoré z nich jasne demonštruje vytvorený graf (pozri obr. 195). Napríklad neprítomnosť parity alebo nepárnosti funkcie geometricky súvisí s nedostatočnou symetriou grafu vo vzťahu k osi y alebo relatívne k začiatku.
Akákoľvek funkcia tvaru y = a x, kde a > 1, má podobné vlastnosti. Na obr. Zostrojilo sa 196 v jednom súradnicovom systéme, grafy funkcií y=2 x, y=3 x, y=5 x.
Pozrime sa teraz na funkciu a vytvorte pre ňu tabuľku hodnôt:
Označme si body na súradnicovej rovine (obr. 197), vyznačujú určitú úsečku, nakreslíme ju (obr. 198).
Vlastnosti funkcie
1)
2) nie je párne ani nepárne;
3) klesá;
4) neobmedzené zhora, obmedzené zdola;
5) neexistuje ani najväčšia, ani najmenšia hodnota;
6) kontinuálne;
7)
8) konvexné smerom nadol.
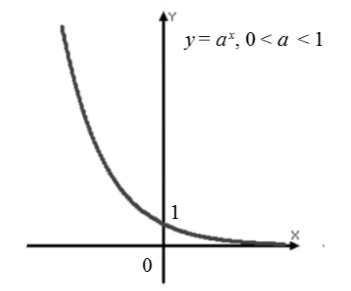
Každá funkcia tvaru y = a x má podobné vlastnosti, kde O<а <1. На рис. 200 в одной системе координат построены графики функций 
Poznámka: funkčné grafy 
tie. y=2 x, symetrické podľa osi y (obr. 201). Je to dôsledok všeobecného tvrdenia (pozri § 13): grafy funkcií y = f(x) a y = f(-x) sú symetrické podľa osi y. Podobne aj grafy funkcií y = 3 x a
Aby sme zhrnuli, čo bolo povedané, uvedieme definíciu exponenciálnej funkcie a zdôrazníme jej najdôležitejšie vlastnosti.
Definícia. Funkcia formy sa nazýva exponenciálna funkcia.
Základné vlastnosti exponenciálnej funkcie y = a x
Graf funkcie y=a x pre a> 1 je na obr. 201 a za 0<а < 1 - на рис. 202.
Krivka znázornená na obr. 201 alebo 202 sa nazýva exponent. V skutočnosti matematici zvyčajne nazývajú samotnú exponenciálnu funkciu y = a x. Takže výraz "exponent" sa používa v dvoch významoch: ako na pomenovanie exponenciálnej funkcie, tak aj na pomenovanie grafu exponenciálnej funkcie. Zvyčajne je význam jasný, či už hovoríme o exponenciálnej funkcii alebo o jej grafe.
Venujte pozornosť geometrickej vlastnosti grafu exponenciálnej funkcie y=ax: os x je horizontálna asymptota grafu. Pravda, toto tvrdenie sa zvyčajne objasňuje nasledovne.
Os x je horizontálna asymptota grafu funkcie
Inými slovami
Prvá dôležitá poznámka. Školáci si často zamieňajú pojmy: mocenská funkcia, exponenciálna funkcia. Porovnaj:
Toto sú príklady mocenských funkcií; 
Toto sú príklady exponenciálnych funkcií.
Vo všeobecnosti y = x r, kde r je konkrétne číslo, je mocninová funkcia (argument x je obsiahnutý v základe stupňa);
y = a", kde a je konkrétne číslo (kladné a odlišné od 1), je exponenciálna funkcia (argument x je obsiahnutý v exponente).
"Exotická" funkcia ako y = x" sa nepovažuje za exponenciálnu ani mocninu (niekedy sa nazýva exponenciálna).
Druhá dôležitá poznámka. Zvyčajne sa neuvažuje o exponenciálnej funkcii so základom a = 1 alebo so základom a, ktorá spĺňa nerovnosť a<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0 a a Faktom je, že ak a = 1, potom pre ľubovoľnú hodnotu x platí rovnosť Ix = 1 Exponenciálna funkcia y = a" s a = 1 "degeneruje" na konštantnú funkciu y = 1 - toto. nie je zaujímavé, ak a = 0, potom 0x = 0 pre akúkoľvek kladnú hodnotu x, t.j. dostaneme funkciu y = 0, definovanú pre x > 0 - to je tiež nezaujímavé, ak a.<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.
Skôr než prejdeme k riešeniu príkladov, všimnite si, že exponenciálna funkcia sa výrazne líši od všetkých funkcií, ktoré ste doteraz študovali. Ak chcete dôkladne preštudovať nový objekt, musíte ho zvážiť z rôznych uhlov, v rôznych situáciách, takže príkladov bude veľa.
Príklad 1
Riešenie, a) Po zostrojení grafov funkcií y = 2 x a y = 1 v jednom súradnicovom systéme si všimneme (obr. 203), že majú jeden spoločný bod (0; 1). To znamená, že rovnica 2x = 1 má jeden koreň x = 0.
Takže z rovnice 2x = 2° dostaneme x = 0.
b) Po zostrojení grafov funkcií y = 2 x a y = 4 v jednom súradnicovom systéme si všimneme (obr. 203), že majú jeden spoločný bod (2; 4). To znamená, že rovnica 2x = 4 má jeden koreň x = 2.
Takže z rovnice 2 x = 2 2 dostaneme x = 2.
c) a d) Na základe rovnakých úvah sme dospeli k záveru, že rovnica 2 x = 8 má jeden koreň a na jej nájdenie nie je potrebné zostavovať grafy zodpovedajúcich funkcií;
je jasné, že x = 3, pretože 2 3 = 8. Podobne nájdeme jediný koreň rovnice
Takže z rovnice 2x = 2 3 sme dostali x = 3 a z rovnice 2 x = 2 x sme dostali x = -4.
e) Graf funkcie y = 2 x sa nachádza nad grafom funkcie y = 1 pre x >0 - je to dobre čitateľné na obr. 203. To znamená, že riešením nerovnice 2x > 1 je interval
e) Graf funkcie y = 2 x sa nachádza pod grafom funkcie y = 4 v bode x<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
Pravdepodobne ste si všimli, že základom pre všetky závery pri riešení príkladu 1 bola vlastnosť monotónnosti (zvýšenie) funkcie y = 2 x. Podobná úvaha nám umožňuje overiť platnosť nasledujúcich dvoch teorémov.
Riešenie. Môžete postupovať takto: vytvorte graf funkcie y-3 x, potom ho roztiahnite od osi x o faktor 3 a potom výsledný graf zdvihnite o 2 jednotky mierky. Je však pohodlnejšie použiť skutočnosť, že 3- 3* =3 *+1, a teda zostaviť graf funkcie y=3 x*1 + 2.
Presuňme sa, ako sme v takýchto prípadoch už mnohokrát urobili, k pomocnému súradnicovému systému s počiatkom v bode (-1; 2) - bodkované čiary x = - 1 a 1x = 2 na obr. 207. „Prepojme“ funkciu y=3* s novým súradnicovým systémom. Ak to chcete urobiť, vyberte kontrolné body pre funkciu 
, ale postavíme ich nie v starom, ale v novom súradnicovom systéme (tieto body sú vyznačené na obr. 207). Potom z bodov zostrojíme exponent - to bude požadovaný graf (pozri obr. 207).
Na nájdenie najväčšej a najmenšej hodnoty danej funkcie na segmente [-2, 2] využívame skutočnosť, že daná funkcia je rastúca, a preto naberá svoje najmenšie, resp. ľavý a pravý koniec segmentu.
Takže:
Príklad 4. Riešte rovnice a nerovnice:
Riešenie, a) Zostrojme grafy funkcií y=5* a y=6-x v jednom súradnicovom systéme (obr. 208). Pretínajú sa v jednom bode; súdiac podľa kresby ide o bod (1; 5). Kontrola ukazuje, že v skutočnosti bod (1; 5) spĺňa rovnicu y = 5* aj rovnicu y = 6-x. Úsečka tohto bodu slúži ako jediný koreň danej rovnice.
Takže rovnica 5 x = 6 - x má jeden koreň x = 1.
b) a c) Exponent y-5x leží nad priamkou y=6-x, ak x>1, je to dobre viditeľné na obr. 208. To znamená, že riešenie nerovnosti 5*>6 možno zapísať takto: x>1. A riešenie nerovnosti 5x<6 - х можно записать так: х < 1.
Odpoveď: a)x = 1; b) x > 1; c)x<1.
Príklad 5. Daná funkcia 
Dokáž to 
Riešenie. Podľa stavu Máme.
1. Exponenciálna funkcia je funkcia tvaru y(x) = a x v závislosti od exponentu x s konštantnou hodnotou základne stupňa a, kde a > 0, a ≠ 0, xϵR (R je množina reálnych čísel).
Uvažujme graf funkcie, ak základ nespĺňa podmienku: a>0
a) a< 0
Ak a< 0 – возможно возведение в целую степень или в рациональную степень с нечетным показателем.
a = -2
Ak a = 0, funkcia y = je definovaná a má konštantnú hodnotu 0
c) a = 1
Ak a = 1, funkcia y = je definovaná a má konštantnú hodnotu 1
Funkčná doména (DOF) Rozsah povolených funkčných hodnôt (APV) 3. Nuly funkcie (y = 0) 4. Priesečníky so zvislou osou oy (x = 0) 5. Zvyšovanie, znižovanie funkcií Ak , potom funkcia f(x) rastie 6. Párna, nepárna funkcia Funkcia y = nie je symetrická vzhľadom na os 0y a vzhľadom na počiatok súradníc, preto nie je ani párna, ani nepárna. (všeobecná funkcia) 7. Funkcia y = nemá žiadne extrémy 8. Vlastnosti stupňa so skutočným exponentom: Nech a > 0; a≠1 Potom pre xϵR; yϵR: Vlastnosti stupňa monotónnosti: ak, tak Ak a> 0, potom . 9. Relatívna poloha funkcie Čím väčšia je základňa a, tým bližšie k osám x a oy a > 1, a = 20 Príklad 1 Najprv si predstavme definíciu exponenciálnej funkcie. Exponenciálna funkcia $f\left(x\right)=a^x$, kde $a >1$. Predstavme si vlastnosti exponenciálnej funkcie pre $a >1$. \ \[bez koreňov\] \ Priesečník so súradnicovými osami. Funkcia nepretína os $Ox$, ale pretína os $Oy$ v bode $(0,1)$. $f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$ \ \[bez koreňov\] \ Graf (obr. 1). Obrázok 1. Graf funkcie $f\left(x\right)=a^x,\ for\ a >1$. Predstavme si vlastnosti exponenciálnej funkcie pri $0 Oblasťou definície sú všetky reálne čísla. $f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- funkcia nie je ani párna, ani nepárna. $f(x)$ je spojité v celej doméne definície. Rozsah hodnôt je interval $(0,+\infty)$. $f"(x)=\vľavo(a^x\vpravo)"=a^xlna$ \ \[bez koreňov\] \ \[bez koreňov\] \ Funkcia je konvexná v celej oblasti definície. Správanie na koncoch domény: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\] Graf (obr. 2). Preskúmajte a nakreslite funkciu $y=2^x+3$. Riešenie. Urobme štúdiu pomocou vyššie uvedeného vzorového diagramu: Oblasťou definície sú všetky reálne čísla. $f\left(-x\right)=2^(-x)+3$ -- funkcia nie je ani párna, ani nepárna. $f(x)$ je spojité v celej doméne definície. Rozsah hodnôt je interval $(3,+\infty)$. $f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$ Funkcia sa zvyšuje v celej oblasti definície. $f(x)\ge 0$ v celej doméne definície. Priesečník so súradnicovými osami. Funkcia nepretína os $Ox$, ale pretína os $Oy$ v bode ($0,4)$ $f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$ Funkcia je konvexná v celej oblasti definície. Správanie na koncoch domény: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\] Graf (obr. 3). Obrázok 3. Graf funkcie $f\left(x\right)=2^x+3$ Nájdite hodnotu výrazu pre rôzne racionálne hodnoty premennej x=2; 0; -3; - Všimnite si, že bez ohľadu na to, aké číslo dosadíme za premennú x, vždy dokážeme nájsť hodnotu tohto výrazu. To znamená, že uvažujeme o exponenciálnej funkcii (E sa rovná trom k mocnine x), definovanej na množine racionálnych čísel: . Zostavme graf tejto funkcie zostavením tabuľky jej hodnôt. Nakreslite hladkú čiaru prechádzajúcu týmito bodmi (obrázok 1) Pomocou grafu tejto funkcie zvážme jej vlastnosti: 3. Zvyšuje sa v celej oblasti definície. 8. Funkcia je konvexná smerom nadol. Ak zostrojíme grafy funkcií v jednom súradnicovom systéme; y=(y sa rovná dvom mocnine x, y sa rovná piatim mocnine x, y sa rovná siedmim mocnine x), potom môžete vidieť, že majú rovnaké vlastnosti ako y= (y sa rovná trom mocnine x) (obr. .2), to znamená, že všetky funkcie tvaru y = (a sa rovná a x mocnine pre väčšie ako jedna) budú mať takéto vlastnosti Nakreslíme funkciu: 1. Zostavenie tabuľky jeho hodnôt. Označme získané body na súradnicovej rovine. Nakreslíme hladkú čiaru prechádzajúcu týmito bodmi (obrázok 3). Pomocou grafu tejto funkcie naznačíme jej vlastnosti: 1. Definičný obor je množina všetkých reálnych čísel. 2. Nie je párne ani nepárne. 3. Znižuje sa v celej oblasti definície. 4. Nemá najväčšie ani najmenšie hodnoty. 5. Obmedzené nižšie, ale nie obmedzené vyššie. 6. Nepretržitý v celej oblasti definície. 7. rozsah hodnôt od nuly do plus nekonečna. 8. Funkcia je konvexná smerom nadol. Podobne, ak zostrojíme grafy funkcií v jednom súradnicovom systéme; y = (y sa rovná jednej polovici mocniny x, y sa rovná jednej pätine mocniny x, y sa rovná jednej sedmine mocniny x), potom si môžete všimnúť, že majú rovnaké vlastnosti ako y = (y sa rovná jednej tretine mocniny x (obr. 4), teda všetky funkcie tvaru y = (y sa rovná jednej delené mocninou a a x, pričom väčší ako nula, ale menší ako jeden) bude mať takéto vlastnosti. Zostrojme grafy funkcií v jednom súradnicovom systéme To znamená, že grafy funkcií y=y= budú tiež symetrické (y sa rovná a rovná mocnine x a y sa rovná jednej delené mocninou a ku x) pre rovnakú hodnotu a. Zhrňme, čo bolo povedané, definovaním exponenciálnej funkcie a uvedením jej hlavných vlastností: Definícia: Funkcia tvaru y=, kde (y sa rovná a mocnine x, kde a je kladné a odlišné od jednotky), sa nazýva exponenciálna funkcia. Je potrebné si zapamätať rozdiely medzi exponenciálnou funkciou y= a mocninnou funkciou y=, a=2,3,4,…. zvukovo aj vizuálne. Exponenciálna funkcia X je sila a pre mocenskú funkciu X je základ. Príklad 1: Vyriešte rovnicu (tri na mocninu x sa rovná deväť) (Y sa rovná tri mocnine X a Y sa rovná deviatim) Obr Všimnite si, že majú jeden spoločný bod M (2;9) (em so súradnicami dva; deväť), čo znamená, že úsečka bodu bude koreňom tejto rovnice. To znamená, že rovnica má jeden koreň x = 2. Príklad 2: Vyriešte rovnicu V jednom súradnicovom systéme zostrojíme dva grafy funkcie y= (y sa rovná piatim mocnine x a y jednej dvadsaťpäťke) Obr. Grafy sa pretínajú v jednom bode T (-2; (te so súradnicami mínus dva; jedna dvadsiata pätina). To znamená, že koreň rovnice je x = -2 (číslo mínus dva). Príklad 3: Vyriešte nerovnicu V jednom súradnicovom systéme zostrojíme dva grafy funkcie y= (Y sa rovná tri na mocninu X a Y sa rovná dvadsiatim siedmim). Obr.9 Graf funkcie sa nachádza nad grafom funkcie y=at x Riešením nerovnosti je teda interval (od mínus nekonečna do troch) Príklad 4: Vyriešte nerovnicu V jednom súradnicovom systéme zostrojíme dva grafy funkcie y= (y sa rovná jednej štvrtine mocniny x a y sa rovná šestnástim). (obr. 10). Grafy sa pretínajú v jednom bode K (-2;16). To znamená, že riešením nerovnosti je interval (-2; (od mínus dva do plus nekonečno), keďže graf funkcie y= sa nachádza pod grafom funkcie v bode x Naša úvaha nám umožňuje overiť platnosť nasledujúcich teorémov: Téma 1: Ak platí vtedy a len vtedy, ak m=n. Veta 2: Ak je pravda vtedy a len vtedy, nerovnosť je pravdivá vtedy a len vtedy (obr. *) Veta 4: Ak platí vtedy a len vtedy (obr.**), nerovnosť je pravdivá vtedy a len vtedy Veta 3: Ak platí vtedy a len vtedy, keď m=n. Príklad 5: Nakreslite graf funkcie y= Upravme funkciu aplikáciou vlastnosti stupňa y= Zostrojme dodatočný súradnicový systém a v novom súradnicovom systéme zostrojíme graf funkcie y = (y sa rovná dvom mocnine x) Obr. Príklad 6: Vyriešte rovnicu V jednom súradnicovom systéme zostrojíme dva grafy funkcie y= (Y sa rovná siedmim mocnine X a Y sa rovná ôsmim mínus X) Obr. Grafy sa pretínajú v jednom bode E (1; (e so súradnicami jedna; sedem) To znamená, že koreň rovnice je x = 1 (x sa rovná jednej). Príklad 7: Vyriešte nerovnicu V jednom súradnicovom systéme zostrojíme dva grafy funkcie y= (Y sa rovná jednej štvrtine mocniny X a Y sa rovná X plus päť). Graf funkcie y=je umiestnený pod grafom funkcie y=x+5, keď riešením nerovnosti je interval x (od mínus jedna do plus nekonečno).
2. Pozrime sa bližšie na exponenciálnu funkciu:
0
Ak , potom funkcia f(x) klesá
Funkcia y= , pri 0
Vyplýva to z vlastností monotónnosti mocniny s reálnym exponentom.
b > 0; b≠1
Napríklad:
Exponenciálna funkcia je spojitá v akomkoľvek bode ϵ R.
Ak a0, potom má exponenciálna funkcia tvar blízky y = 0.
Ak a1, potom ďalej od osí ox a oy a graf nadobudne tvar blízky funkcii y = 1.
Zostrojte graf y =
Exponenciálna funkcia $f\left(x\right)=a^x$, kde $0
Príklad úlohy na zostrojenie exponenciálnej funkcie
