Презентация на тема "комбинации". Презентация за урок по алгебра и принципи на анализ на тема "Комбинаторика: движения, пермутации, комбинации" Комбинации с повторения

„Задачи на комбинаториката“ - По колко начина може да се избере една книга? По колко начина може да се формира екипаж на кораб, състоящ се от командир и инженер? Комбинаторика. Задача № 2. К. Правило за събиране Правило за умножение. Правило за сумата. Решение: 30 + 40 = 70 (по начини). Задача No1. Задача № 3. I. Нека има трима кандидати за поста командир и 2 за поста инженер.

“Поставяне на елементи” - Комбинаторика. Настаняване. Поставяне и комбиниране. Формули: За всякакви естествени числа n и k, където n>k, са валидни равенствата: За броя на изборите на два елемента от n данни: Комбинация. В комбинаториката комбинация от n до k е набор от k елемента, избрани от дадени n елемента.

“Статистически характеристики” - Математическа статистика и др. Статистически изследвания. 5. Какво е статистика? 3. 9. Средно аритметично Range Mode Median. Етапи на изследователската дейност. 2. 14. „Има три вида лъжи: обикновени лъжи, явни лъжи и статистически лъжи. "

„Комбинации“ - Има букви A, B, C, D. правете всички комбинации само от две букви. Самостоятелната работа се състоеше от 2 задачи. Задачата е решена правилно от 13 ученици, а примерът е 17. 3 ученици не успяха да завършат работата. Комбинаторни задачи. Задача No1. Колко ученици успешно решиха самостоятелна работа. Писането на работата отне 30 студенти.

“Пермутации на елементи” - Директен алгоритъм за лексикографско изброяване на пермутации. Комбинаторика. Най-големият проблем с нарастващата подпоследователност. Номерация на комплекта. Формално описание на алгоритъма. Пренареждания. Теорема за лексикографско изброяване на пермутации. Изброяване на пермутации. Изброяване на пермутации чрез елементарни транспозиции.

„Комбинаторика 9 клас” - От 30 участници събранието трябва да избере председател и секретар. Решение: а) 3! = 1 · 2 · 3 =6 б) 5! = 1 · 2 · 3 · 4 · 5 = 120. II. Обозначение: P n Формула за изчисляване на пермутации: P n = A6 10 =n ·(n -1) · (n-2) · … · 3 · 2 · 1=n! 2-ра група. Обозначение: Формула за изчисляване на комбинации: *. Отговори и решения. 2-ра група.

В темата има общо 25 презентации

КОМБИНАТОРИКА

Цели на урока:

Разберете какво изучава комбинаториката
Разберете как е възникнала комбинаториката
Изучавайте комбинаторни формули и се научете как да ги прилагате при решаване на задачи

Раждането на комбинаториката като клон на математиката се свързва с трудовете на Блез Паскал и Пиер Ферма върху теорията на хазарта.

Блез Паскал

Пиер Ферма

Голям принос за развитието на комбинаторните методи направи G.V. Лайбниц, Й. Бернули и Л. Ойлер.

Г.В. Лайбниц

Л. Ойлер.

Й. Бернули

Лема. Нека множеството A има m елемента, а множеството B има n елемента. Тогава броят на всички отделни двойки (a,b), където a\in A,b\in B ще бъде равен на mn. Доказателство. Наистина, с един елемент от множеството A можем да направим n такива различни двойки, като общо има m елемента в множеството A.

Разположения, пермутации, комбинации Нека имаме набор от три елемента a,b,c. По какви начини можем да изберем два от тези елементи? ab,ac,bc,ba,ca,cb.

Пренареждания Ще ги пренаредим по всички възможни начини (броят на обектите остава непроменен, променя се само редът им). Получените комбинации се наричат пермутации, а броят им е равен на Пн = н! =1 · 2 · 3 · ... · ( n-1)n

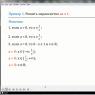
Символът n! се нарича факториел и означава произведението на всички цели числа от 1 до n. По дефиниция се смята, че 0!=1 1!=1 Пример за всички пермутации на n=3 обекта (различни фигури) е на снимката. По формулата трябва да има точно P3=3!=1⋅2⋅3=6 , и ето какво се случва.

С увеличаването на броя на обектите, броят на пермутациите расте много бързо и става трудно да се изобразят ясно. Например, броят на пермутациите на 10 елемента вече е 3628800 (повече от 3 милиона!).

Разположения Нека има n различни обекта. Ще изберем m обекта от тях и ще ги пренаредим по всички възможни начини (тоест ще се промени както съставът на избраните обекти, така и техният ред). Получените комбинации се наричат разположения на n обекта по m, а броят им е Aⁿm =n!(n−m)!=n⋅(n−1)⋅...⋅(n−m+1)

Определение. Чрез поставяне на набор от n различни елемента в m елемента (m ≤ н) са наречени комбинации , които са съставени от дадени n елемента по m елемента и се различават или по самите елементи, или по реда на елементите.

Комбинации Нека има n различни обекта. Ще изберем m обекта от тях по всеки възможен начин (т.е. съставът на избраните обекти се променя, но редът не е важен). Получените комбинации се наричат комбинации от n обекта по m, а броят им е Cmn=n!(n−m)!⋅m!

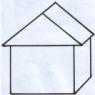
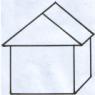
Пример за всички комбинации от n=3 обекта (различни фигури) по m=2 е на снимката по-долу. Според формулата трябва да има точно C23=3!(3−2)!⋅2!:3!=3. Ясно е, че винаги има по-малко комбинации от разположенията (тъй като редът е важен за разположенията, но не и за комбинациите), и конкретно в m! пъти, тоест формулата за свързване е правилна: Amn=Cmn⋅Pm.

Метод 1. В една игра участват 2 души, следователно трябва да изчислите по колко начина можете да изберете 2 души от 15, като редът в такива двойки не е важен. Нека използваме формулата, за да намерим броя на комбинациите (проби, които се различават само по състав) от n различни елемента от m елемента всяка

n!= 1⋅ 2 ⋅3⋅...⋅ n , с n=2, m=13.

Метод 2.Първият играч изигра 14 игри (2-ра, 3-та, 4-та и така нататък до 15-та), вторият играч изигра 13 игри (3-та, 4-та и т.н. до 15-та). Е, изключваме факта, че вече е имало игра с първият), 3-ти играч - 12 игри, 4-ти - 11 игри, 5 - 10 игри, 6 - 9 игри, 7 - 8 игри, 8 - 7 игри,

а 15-та вече е играла с всички.

Общо: 14+13+12+11+10+9+8+7+6+5+4+3+2+1=105 игри

ОТГОВОР. 105 игри.

Учител по математика Светлана Валериевна Аксенова

Бугровская гимназия, район Всеволожск, Ленинградска област

За да използвате визуализации на презентации, създайте акаунт в Google и влезте в него: https://accounts.google.com

Надписи на слайдове:

Комбинации

Комбинации Броят на всички селекции на n елемента от m данни, без да се взема предвид редът, се нарича броят на комбинациите от m елемента по n. Всички комбинации се различават една от друга поне по един елемент; Редът на елементите тук не е важен; Разликата между комбинация и подредба е, че ако пренаредите елементите в подредба, ще получите различна подредба, но комбинацията не зависи от реда на елементите, включени в нея.

Комбинации Броят на всички селекции на n елемента от m данни, без да се взема предвид редът, се нарича броят на комбинациите от m елемента по n. Намерете: Брой комбинации от 6 до 3: Брой комбинации от 4 до 4:

Задача No1 От 20 ученици трябва да изберете двама дежурни. По колко начина може да стане това? Решение: Трябва да изберем двама от 20. Ясно е, че нищо не зависи от реда на избор, тоест Иванов - Петров или Петров - Иванов са една и съща двойка дежурни. Следователно това ще бъдат комбинации от 20 на 2.

Задача No2. Минотавърът има 25 затворници, които гневят в лабиринта. а) По колко начина може да избере три от тях за закуска, обяд и вечеря? б) Колко начина има да бъдат освободени трима пленници? Решение: A) Редът е важен. Б) Редът не е важен

Задача № 3 В класа има 27 ученици, трябва да се изберат трима от тях. По колко начина може да стане това, ако: а) първият ученик трябва да реши задачата, вторият да отиде за тебешир, третият да дежури в столовата; б) трябва ли да пеят в хор? 6

По колко различни начина може да се сформира отбор от двама от седем члена на клуб по математика, който да участва в олимпиадата? Задача No4

Задача № 5 Отделът разполага с 5 ръководни и 8 старши служители. Да се командироват двама водещи и двама старши научни работници. По колко начина може да се направи избор?

От разбъркано тесте от 36 карти се изтеглят 4 карти на случаен принцип. Каква е вероятността всички изтеглени карти да са аса? Проблем №6

Задача № 7 В партида от 50 части има 10 дефектни. От партидата се изваждат произволно четири части. Определете вероятността всичките 4 части да бъдат дефектни. Общо резултати: Благоприятни резултати: Вероятност.

Пренареждания Разположения Комбинации Вероятност

Общинска образователна институция Средно училище № 30, Волгоград

Учителят по математика Склейнова Н.И.

Факториал

Определение 1

Факториелът е произведението на първите n естествени числа

н! = 1*2*2*…(n-2)(n-1)n

2!=1*2=2

3!=1*2*3=6

4!= 1*2*3*4=24

5!=1*2*3*4*5=120

Пренареждания

Определение 2

Пермутация от n елемента е всяко подреждане на тези елементи в определен ред P=n!

Пример 1

По колко начина могат да бъдат поставени 8-те участници във финалното състезание на осем бягащи пътеки?

Р 8 =8!=1*2*3*4*5*6*7*8= 40320 (начини)

Разположения

Определение 3

Подреждане на n елемента по k (k≤ n) е всяко множество, състоящо се от всякакви k елемента, взети в определен ред от дадените n елемента

Пример 2

Учениците от втори клас изучават 8 предмета. По колко начина можете да създадете график за един ден, така че да включва 4 различни предмета?

А 8 4 =8*7*6*5= 1680 (начини)

А н к =

Комбинации

Определение 4

Комбинация от n елемента от k е всяко множество, съставено от k елемента, избрани от дадените n елемента

СЪС н к =

Пример 3

От 15-те членове на туристическата група трябва да бъдат избрани трима дежурни. По колко начина може да се направи този избор?

СЪС 15 3 =15!/(3!*12!)=(13*14*15)/(1*2*3)= 455 (начини)

Вероятност

Определение 5

Вероятността за събитие A е съотношението на броя на благоприятните резултати N(A) от тест към броя на всички еднакво възможни резултати N

P(A)= N(A)/N

Пример 4

От 25 изпитни работи по геометрия ученикът е подготвил 11 първи и 8 последни работи. Каква е вероятността на изпита да получи билет, който не е подготвил?

P(A)=(25-11-8)/25= 0,24

Добавяне на вероятности

Определение 6

Ако събитие C означава, че се случва едно от две несъвместими събития: A или B, тогава вероятността за събитие C е равна на сбора от вероятностите за събития A и B

P(C)=P(A)+P(B)

Сумата от вероятностите за противоположни събития е 1

P(A)+P( А )=1

Умножаване на вероятностите

Определение 7

Ако събитие C означава съвместно възникване на две независими събития A и B, тогава вероятността за събитие C е равна на произведението на вероятностите за събития A и B

P(C)=P(A)*P(B)

Вероятност

Сума от вероятности

Сумата от вероятностите за две събития е равна на сумата от вероятността от произведението на тези събития и вероятността от сумата от тези събития

P(A)+P(B)= P(A*B) +P(A+B)

Вероятност за сумата

Вероятността за сумата от две събития е равна на разликата между сумата от вероятностите за тези събития и произведението на вероятностите за тези събития

P(A+B)=P(A)+P(B)-P(A)*P(B)

Проблем 1

Решение

Състояние

Вероятност за всеки хитове равна на 0,8.

Биатлонист стреля по мишени 5 пъти. Вероятността за попадение в целта с един изстрел е 0,8. Намерете вероятността биатлонистът да уцели мишените първите 3 пъти и да пропусне последните 2 пъти. Закръглете резултата до стотни.

Вероятност за всеки мис равно на 1-0,8= 0,2 .

Използвайки формулата за умножение на вероятността, получаваме

P(A )=0,8*0,8*0,8*0,2*0,2

P(A )= 0,02048 0,02

Отговор: 0,02

Проблем 2

Състояние

Решение

В Страната на приказките има два вида време: добро и отлично, като времето, веднъж установено сутрин, остава непроменено през целия ден. Известно е, че с вероятност 0,6 времето утре ще бъде същото като днес. Днес е 18 септември, времето в Приказната страна е хубаво. Намерете вероятността времето да е страхотно в Страната на приказките на 21 септември.

Тъй като на 18 септември времето е добро, то на 19 септември времето е добро с вероятност 0,6 и отлично с вероятност 0,4.

Ако на 19 септември времето е хубаво, то на 20 септември вероятността за добро време е 0,6*0,6=0,36

Вероятността за отлично време е 0,6*0,4=0,24

По същия начин, ако времето е отлично на 19 септември, тогава с вероятност от 0,4 * 0,6 = 0,24 то ще бъде отлично на 20 септември. Вероятността за хубаво време на 20 септември е 0,4*0,4=0,16.

Разсъждавайки по подобен начин, намираме, че вероятността за отлично време на 21 септември ще бъде равна на вероятността от сбора: 0,6*0,24+ +0,6*0,24+0,4*0,16+0,6*0,24= 0,496

Проблем 3

Състояние

Решение

Автоматична линия произвежда батерии. Вероятността завършената батерия да е дефектна е 0,02. Преди опаковането всяка батерия преминава през контролна система. Вероятността системата да блокира дефектна батерия е 0,98. Вероятността системата по погрешка да блокира работеща батерия е 0,03. Намерете вероятността произволно избрана произведена батерия да бъде блокирана от системата за управление.

Нека събитието A = (батерията ще бъде блокирана), тогава вероятността за настъпване на това събитие може да се намери като обединение на пресечните точки на събития.

P(A)=0,02*0,98+0,98*0,03

P(A)=0,98(0,02+0,03)

P(A)=0,98*0,05= 0,049

Отговор: 0,049

Литература

Макаричев Ю.Н. Алгебра: елементи на статистиката и теория на вероятностите: учебник. помагало за ученици от общото образование. институции. Издателство "Просвещение", 2003 г

Мордкович А.Г., Семенов П.В. Алгебра и началото на математическия анализ. Част 1. Учебник за общообразователни организации. Издателство "Мнемозина", 2015 г

Лисенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка за Единния държавен изпит 2016 г. Издателство "Легион" LLC, 2015 г

Висоцки И.Р., Яшченко И.В. Единен държавен изпит 2016. Математика. Теория на вероятностите. Работна тетрадка. Издателство МЦНМО, 2016г

1. Организационен момент
Поздравяване на учениците, съобщаване на темата и целта на урока
2. Повторение и затвърдяване на преминатия материал
· Отговори на въпроси за домашна работа (анализ на нерешени задачи).
· Проследяване на усвояването на материала (писмено проучване).
Опция 1
1. Надеждно събитие и неговата вероятност.
2. а) При произволен експеримент се хвърлят два зара. Намерете вероятността сборът да бъде 7 точки. Закръглете резултата до стотни.
б) В първенството по гимнастика участват 40 спортисти: 12 от Аржентина, 9 от Бразилия, останалите от Парагвай. Редът на представяне на гимнастичките се определя чрез жребий. Намерете вероятността спортистът, който се състезава първи, да е от Парагвай.
в) Средно от 500 продадени градински помпи, 4 текат. Намерете вероятността една произволно избрана за контрол помпа да не изтече.
опция 2
1. Невъзможно събитие и неговата вероятност.
2. а) При произволен експеримент се хвърлят два зара. Намерете вероятността сборът да бъде 9 точки. Закръглете резултата до стотни.
б) В първенството по гимнастика участват 64 спортисти: 20 от Япония, 28 от Китай, останалите от Корея. Редът на представяне на гимнастичките се определя чрез жребий. Намерете вероятността спортистът, който се състезава първи, да е от Корея.
в) Фабриката произвежда чанти. Средно на всеки 170 качествени торби се падат шест торби със скрити дефекти. Намерете вероятността закупената чанта да бъде с високо качество. Закръглете резултата до стотни.

Отговор: вариант 1. 2. а) 0,17; б) 0,475; в) 0,992.
вариант 2. 2. а) 0,11; б) 0,25; в) 0,97.
3. Учене на нов материал
Класът беше разделен на групи, които събраха информация, обобщиха и представиха резултатите от работата си в клас (учениците представят резултатите от работата си).
1 група(намерете информация за това какви фактори (причини) са допринесли за появата на науката за комбинаториката, кои учени са били в началото на нейното възникване).
2-ра група(намерете информация дали комбинаториката съществува в реалния живот и ако да, в кои отрасли се използва).

3 група (намерете информация за това кои проблеми се наричат комбинаторни и как могат да бъдат решени, разгледайте всеки метод за решаване и направете селекция от няколко проблема, решени с определен метод).
3.1. 1 група.
Представители на голямо разнообразие от специалности трябва да решават задачи, които включват определени комбинации, съставени от букви, цифри и други обекти.
Когато разглеждахме най-простите вероятностни проблеми, трябваше да преброим броя на различните резултати (комбинации). За малък брой елементи такива изчисления са лесни за извършване. В противен случай подобна задача представлява значителна трудност. (слайд 1)

Комбинаторикае дял от математиката, който изучава въпроси относно броя на различни комбинации (отговарящи на определени условия), които могат да бъдат направени от дадени елементи.
Комбинаторика- клон на математиката, в който се изучават най-простите „връзки“. Пермутациите са съединения, които могат да бъдат съставени от n обекта, променяйки техния ред по всички възможни начини; броят на техните разположения - съединения, съдържащи m обекта от даденото число n, различаващи се или в реда на обектите, или в самите обекти; техният брой Комбинации - съединения, съдържащи m елемента от n, различаващи се един от друг в поне един елемент (в съвременния тълковен речник, издаден от „Голяма съветска енциклопедия“).
Хората са се сблъсквали с проблеми, при които е трябвало да изберат определени предмети, да ги подредят в определен ред и да намерят най-доброто сред различни подредби още в праисторическата епоха, да изберат най-добрата позиция за ловци по време на лов, воини по време на битка, инструменти по време на работа. . (слайд 2)

· Терминът „комбинаторика“ е въведен в математическата употреба от Лайбниц, който през 1666 г. публикува своя труд „Беседи за изкуството на комбинирането“. (слайд 3)
· Комбинаториката първоначално възниква през XVI във връзка с разпространението на различни хазартни игри. (слайд 4)
…
3.1. 2-ра група.(слайд 1)
Забележително е, че една наука, която започна с разглеждането на хазарта, обещава да стане най-важният обект на човешкото познание. В края на краищата повечето от житейските въпроси всъщност са проблеми от теорията на вероятностите.
П. Лаплас

Области на приложение на комбинаториката:
. образователни институции (график) (слайд 2)
. ресторантьорство (планиране на менюта)
. лингвистика (разглеждане на опции за буквени комбинации)
. география (оцветяване на карта) (слайд 3)
…
…
3.1. 3 група
Проблеми, които включват определени комбинации от обекти, се наричат комбинативен.(слайд 1)
Правило за добавяне: ако може да се избере някакъв обект Ам начини и може да бъде избран друг обект Bн начини, тогава може да се направи изборът „или А, или Б“. m + n начина.
(слайд 2)
Например:
· В чиния има 5 ябълки и 4 портокала. По колко начина можете да изберете един плод?
Според условията на задачата една ябълка може да бъде избрана по пет начина, портокал по четири. Тъй като проблемът е да се избере „или ябълка, или портокал“, тогава, според правилото за добавяне, това може да се направи по 5 + 4 = 9 начина.
· Нека да разгледаме тази задача: колко двуцифрени числа могат да бъдат съставени от цифрите 1,4,7, като всяка от тях се използва не повече от веднъж при записване на числото? (слайд 3)
· Решение: за да не пропуснем или повторим някое от числата, ще ги напишем във възходящ ред. Първо записваме числата, започвайки с цифрата 1, след това с цифрата 4 и накрая с цифрата 7:
14, 17, 41, 47, 71, 74.
Отговор: 6.
Този метод се нарича изброяване на опциите.Така от тези три цифри могат да се образуват общо 6 различни двуцифрени числа.
Този проблем може да се реши по друг начин. Неговото име - дърво на възможните варианти.За тази задача е изградена специална верига. (слайд 4) (слайд 5)
Поставяме звездичка. Той ще посочи броя на възможните опции.
След това вземаме 3 сегмента от звездичката. В формулировката на задачата са дадени 3 числа - 1, 4, 7.
Поставяме тези числа в краищата на сегментите. Те ще посочат броя на десетиците в дадено число.
След това рисуваме 2 сегмента от всяко число.
В краищата на тези сегменти също пишем числата 1, 4, 7. Те ще посочат броя на единиците.
Нека да разгледаме числата, които получихме: 14, 17, 41, 47, 71, 74. Тоест, получихме общо 6 числа.
Отговор: 6.

Тази диаграма наистина прилича на дърво, макар и „с главата надолу“ и без ствол.
Правило за умножение: ако обект А може да бъде избран м начини и ако след всеки такъв избор обект B може да бъде избран по n начина, тогава може да се извърши изборът на двойката (A, B) в посочения ред m∙н начини. (слайд 6)
· Колко двуцифрени числа могат да се съставят от цифрите 1,4,7, като всяка от тях се използва не повече от веднъж?
Този проблем може да се реши по различен начин и много по-бързо, без да се изгражда дърво от възможни варианти. Нека помислим така. Първата цифра на двуцифрено число може да бъде избрана по три начина. Тъй като след избора на първата цифра ще останат две, втората цифра може да бъде избрана от останалите цифри по два начина. Следователно общият брой на търсените трицифрени числа е равен на произведението 3∙2, т.е. 6.
· Колко петцифрени числа могат да се съставят от числата 5, 9, 0, 6?

Според правилото за умножение получаваме: 4∙4∙4∙4=256 числа.
(слайд 7)
Пренареждания -връзки, всяка от които съдържан различни елементи, взети в определен ред (слайд 8)
Pn=n! = 1 · 2 · 3 · … · (n -2) · (n -1) · n
Задача.(слайд 9)
По колко начина могат да се подредят седем различни книги на един рафт?
Решение:
Броят на тези начини е равен на броя на пермутациите на седем елемента,
тези. P 7 = 7! = 1 · 2 · 3 · … · 7 = 5040.
Отговор: 5040.
Задача.(слайд 10)
Има 10 различни книги, три от които са справочници. По колко начина
Възможно ли е да подредите тези книги на рафт, така че всички справочници да са една до друга?
Решение:
защото Ако справочниците трябва да стоят един до друг, тогава ще ги считаме за една книга. След това трябва да подредите 10 книги на рафта - 3+1=8 книги. Може да се направистр. 8 начини. За всяка от получените комбинации можете да направитеП 3 пренареждане на директории.
Следователно броят на начините за подреждане на книги на рафт е равен на продукта:
P 8 P 3 = 8! · 3! = 40320 · 6 = 241920.
Отговор: 241920.
…
…