Równania i nierówności kwadratowe z parametrem. Podręcznik "Równania i nierówności z parametrami" Równania liniowe i nierówności z parametrami

Na tej lekcji przestudiujemy algorytm rozwiązywania nierówności z parametrami i nauczymy się, jak go zastosować przy rozwiązywaniu tego typu problemów.

Definicja pierwsza.

Rozwiązanie nierówności za pomocą parametru polega na znalezieniu dla każdej wartości parametru zbioru wszystkich rozwiązań danej nierówności lub udowodnieniu, że rozwiązania nie istnieją.

Rozważmy nierówności liniowe.

Definicja druga.

Nierówności postaci a x plus mogą być większe od zera, większe lub równe zero, mniejsze od zera, mniejsze lub równe zero, gdzie A i być są liczbami rzeczywistymi, X- zmienne, nazywane są nierównościami pierwszego stopnia (nierównościami liniowymi).

Algorytm rozwiązywania nierówności liniowej z parametrem, na przykład nierówność x plus jest większa od zera, gdzie A i być są liczbami rzeczywistymi, X- zmienny. Rozważ następujące przypadki:

Pierwszy przypadek:A jest większe od zera, to x jest większe od minus podzielone przez a.

W konsekwencji zbiór rozwiązań nierówności jest otwartym promieniem numerycznym od minus podzielonym przez a do plus nieskończoność.

Drugi przypadek:A mniejsze od zera, to x jest mniejsze od minus podzielone przez a

i dlatego zbiór rozwiązań nierówności jest otwartym promieniem numerycznym od minus nieskończoności do minus podzielonym przez a.

Przypadek trzeci: równa się zero, wówczas nierówność przyjmie postać: zero pomnożone przez x plus będzie większe od zera i for kochanie większa od zera, rozwiązaniem nierówności jest dowolna liczba rzeczywista i kiedy kochanie mniejsza lub równa zero, nierówność nie ma rozwiązań.

Pozostałe nierówności rozwiązuje się analogicznie.

Spójrzmy na przykłady.

Ćwiczenie 1

Rozwiąż nierówność a x jest mniejsze lub równe jeden.

Rozwiązanie

W zależności od znaku A Rozważmy trzy przypadki.

Pierwszy przypadek: jeśli A jest większe od zera, wówczas x jest mniejsze lub równe jedności podzielonej przez a;

Przypadek drugi: jeśli A jest mniejsze od zera, wówczas x jest większe lub równe jedności podzielonej przez a;

Przypadek trzeci: jeśli A jest równe zero, to nierówność przybierze postać: zero pomnożone przez x jest mniejsze lub równe jeden, a zatem każda liczba rzeczywista jest rozwiązaniem pierwotnej nierówności.

Zatem jeśli A jest większe od zera, wówczas x należy do promienia od minus nieskończoności do jedności podzielonej przez a.

Jeśli A A równy zeru,

To X

Odpowiedź: jeśli A jest większe od zera, wówczas x należy do promienia od minus nieskończoności do jedności podzielonej przez a;

Jeśli A jest mniejsze od zera, to x należy do promienia od jedności podzielonego przez a do plus nieskończoność i if A równy zeru,

To X x należy do zbioru liczb rzeczywistych.

Zadanie 2

Rozwiąż moduł nierówności x minus dwa większy niż minus kwadrat różnicy między a a jeden.

Rozwiązanie

Zauważ, że moduł x minus dwa jest większy lub równy zero dla dowolnej liczby rzeczywistej X i minus kwadrat różnicy między a i jeden jest mniejszy lub równy zero dla dowolnej wartości parametru A. Dlatego jeśli A równa się jeden, to dowolne X- liczba rzeczywista inna niż dwa jest rozwiązaniem nierówności, a jeśli A nie jest równa jedności, wówczas rozwiązaniem nierówności jest dowolna liczba rzeczywista.

Odpowiedź: jeśli A równa się jeden, wówczas x należy do sumy dwóch otwartych promieni liczbowych od minus nieskończoności do dwóch i od dwóch do plus nieskończoności,

i jeśli A należy wówczas do sumy dwóch otwartych promieni liczbowych od minus nieskończoności do jeden i od jednego do plus nieskończoności X należy do zbioru liczb rzeczywistych.

Zadanie 3

Rozwiąż nierówność trzykrotną różnicę czterech a i x mniejszych niż dwa a x plus trzy.

Rozwiązanie

Po elementarnych przekształceniach tej nierówności otrzymujemy nierówność: x pomnożone przez sumę dwóch a i trzy jest większe niż trzy pomnożone przez różnicę czterech a i jeden.

Pierwszy przypadek: jeśli dwa plus trzy jest większe od zera, to znaczy A jest większe niż minus trzy sekundy, wówczas x jest większe od ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownik wynosi dwa plus trzy.

Drugi przypadek: jeśli dwa plus trzy jest mniejsze od zera A jest mniejsze niż minus trzy sekundy, wówczas x jest mniejsze od ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownik wynosi dwa plus trzy.

Przypadek trzeci: jeśli dwa a plus trzy równa się zero, to znaczy A równa się minus trzy sekundy,

każda liczba rzeczywista jest rozwiązaniem pierwotnej nierówności.

W konsekwencji, jeśli a należy do otwartej osi liczbowej od minus trzech sekund do plus nieskończoności, to x

należy do otwartej osi liczbowej z ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownik to dwa plus trzy, do plus nieskończoność.

Jeśli a należy do otwartej osi liczbowej od minus nieskończoności do minus trzy sekundy, to x należy do otwartej osi liczbowej od minus nieskończoności do ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownikiem jest dwa plus trzy;

Jeśli A równa się zatem minus trzy sekundy X należy do zbioru liczb rzeczywistych.

Odpowiedź: jeśli a należy do otwartej osi liczbowej od minus trzech sekund do plus nieskończoności, to x

należy do otwartego promienia liczbowego z ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownik to dwa a plus trzy do plus nieskończoność;

jeśli a należy do otwartej osi liczbowej od minus nieskończoności do minus trzy sekundy, to x należy do otwartej osi liczbowej od minus nieskończoności do ułamka, którego licznik jest trzykrotnością różnicy czterech a i jeden, a mianownikiem jest dwa plus trzy;

Jeśli A równa się zatem minus trzy sekundy X należy do zbioru liczb rzeczywistych.

Zadanie 4

Dla wszystkich prawidłowych wartości parametrów A rozwiązać nierówność pierwiastek kwadratowy z x minus a plus pierwiastek kwadratowy z dwóch a minus x plus pierwiastek kwadratowy z minus jeden plus pierwiastek kwadratowy z trzech minus a przez zero.

Rozwiązanie

Znajdźmy dziedzinę definicji parametru A. Wyznacza się to za pomocą układu nierówności, po rozwiązywaniu którego stwierdzamy, że a należy do odcinka od jednego do trzech.

Ta nierówność jest równoważna układowi nierówności, po rozwiązaniu którego stwierdzamy, że x należy do odcinka od a do dwóch a.

Jeżeli a należy do odcinka od jednego do trzech, to rozwiązaniem pierwotnej nierówności jest odcinek od a do dwóch a.

Odpowiedź: jeśli a należy do segmentu od jednego do trzech, toix należy do segmentu od a do dwóch a.

Zadanie 5

Znajdź wszystko A, dla której nierówność

pierwiastek kwadratowy z x kwadrat minus x minus dwa plus pierwiastek kwadratowy ułamka, którego licznikiem jest dwa minus x i mianownikiem jest x plus cztery większy lub równy a x plus dwa minus pierwiastek kwadratowy ułamka, którego licznikiem jest x plus jeden i mianownik to pięć minus x nie ma rozwiązania.

Rozwiązanie

Pierwszy. Obliczmy dziedzinę definicji tej nierówności. Wyznacza go układ nierówności, którego rozwiązaniem są dwie liczby: x jest równe minus jeden i x jest równe dwa.

Drugi. Znajdźmy wszystkie wartości a, dla których ta nierówność ma rozwiązania. Znajdziemy na to wszystko A, dla którego x jest równe minus jeden i x jest równe dwa - to jest rozwiązanie tej nierówności. Rozważmy i rozwiążemy zbiór dwóch systemów. Rozwiązaniem jest połączenie dwóch promieni liczbowych od minus nieskończoności do minus jednej połowy i od jednego do plus nieskończoności.

Oznacza to, że ta nierówność ma rozwiązanie, jeśli a należy do sumy dwóch promieni liczbowych od minus

nieskończoności do minus jednej połowy i od jednego do plus nieskończoności.

Trzeci. W konsekwencji ta nierówność nie ma rozwiązania, jeśli a należy do przedziału od minus pół do jeden.

Odpowiedź: nierówność nie ma rozwiązania, jeśli a należy do przedziału od minus pół do jedności.

Rozwiązywanie nierówności za pomocą parametru.

Nierówności o postaci ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются nierówności liniowe.

Zasady rozwiązywania nierówności liniowych za pomocą parametru są bardzo podobne do zasad rozwiązywania równań liniowych za pomocą parametru.

Przykład 1.

Rozwiąż nierówność 5x – a > ax + 3.

Rozwiązanie.

Najpierw przekształćmy pierwotną nierówność:

5x – ax > a + 3, z nawiasu po lewej stronie nierówności usuńmy x:

(5 – a)x > a + 3. Rozważmy teraz możliwe przypadki dla parametru a:

Jeśli a > 5, to x< (а + 3) / (5 – а).

Jeśli a = 5, to nie ma rozwiązań.

Jeśli< 5, то x >(a + 3) / (5 – a).

To rozwiązanie będzie odpowiedzią na nierówność.

Przykład 2.

Rozwiąż nierówność x(a – 2) / (a ​​– 1) – 2a/3 ≤ 2x – a dla a ≠ 1.

Rozwiązanie.

Przekształćmy pierwotną nierówność:

x(a – 2) / (a ​​– 1) – 2x ≤ 2a/3 – a;

Ах/(а – 1) ≤ -а/3. Mnożąc obie strony nierówności przez (-1), otrzymujemy:

topór/(a – 1) ≥ a/3. Zbadajmy możliwe przypadki dla parametru a:

1 przypadek. Niech a/(a – 1) > 0 lub a € (-∞; 0)ᴗ(1; +∞). Wtedy x ≥ (a – 1)/3.

Przypadek 2. Niech a/(a – 1) = 0, tj. a = 0. Wtedy x jest dowolną liczbą rzeczywistą.

Przypadek 3. Niech a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Odpowiedź: x € [(a – 1)/3; +∞) dla € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] za € (0; 1);
x € R dla a = 0.

Przykład 3.

Rozwiąż nierówność |1 + x| ≤ ax względem x.

Rozwiązanie.

Wynika to z warunku, że prawa strona osi nierówności musi być nieujemna, tj. ax ≥ 0. Zgodnie z zasadą ujawniania modułu z nierówności |1 + x| ≤ ax mamy podwójną nierówność

Oś ≤ 1 + x ≤ Oś. Zapiszmy wynik w postaci układu:

(topór ≥ 1 + x;
(-ax ≤ 1 + x.

Przekształćmy to do:

((a – 1)x ≥ 1;
((a + 1)x ≥ -1.

Powstały układ badamy w odstępach i punktach (ryc. 1):

Dla a ≤ -1 x € (-∞; 1/(a – 1)].

O -1< а < 0 x € [-1/(а – 1); 1/(а – 1)].

Gdy a = 0 x = -1.

O godzinie 0< а ≤ 1 решений нет.

Graficzna metoda rozwiązywania nierówności

Rysowanie wykresów znacznie upraszcza rozwiązywanie równań zawierających parametr. Stosowanie metody graficznej przy rozwiązywaniu nierówności z parametrem jest jeszcze jaśniejsze i wygodniejsze.

Graficzne rozwiązanie nierówności postaci f(x) ≥ g(x) polega na znalezieniu wartości zmiennej x, dla której wykres funkcji f(x) leży nad wykresem funkcji g(x). Aby to zrobić, zawsze konieczne jest znalezienie punktów przecięcia wykresów (jeśli takie istnieją).

Przykład 1.

Rozwiąż nierówność |x + 5|< bx.

Rozwiązanie.

Budujemy wykresy funkcji y = |x + 5| i y = bx (ryc. 2). Rozwiązaniem nierówności będą te wartości zmiennej x, dla których wykres funkcji y = |x + 5| będzie poniżej wykresu funkcji y = bx.

Obrazek przedstawia:

1) Dla b > 1 proste przecinają się. Odcięta punktu przecięcia wykresów tych funkcji jest rozwiązaniem równania x + 5 = bx, skąd x = 5/(b – 1). Wykres y = bx znajduje się powyżej w punkcie x z przedziału (5/(b – 1); +∞), co oznacza, że ​​zbiór ten jest rozwiązaniem nierówności.

2) Podobnie stwierdzamy, że przy -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) Dla b ≤ -1 x € (-∞; 5/(b – 1)).

4) Dla 0 ≤ b ≤ 1 wykresy się nie przecinają, co oznacza, że ​​nierówność nie ma rozwiązań.

Odpowiedź: x € (-∞; 5/(b – 1)) dla b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) przy -1< b < 0;
nie ma rozwiązań dla 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) dla b > 1.

Przykład 2.

Rozwiąż nierówność a(a + 1)x > (a + 1)(a + 4).

Rozwiązanie.

1) Znajdźmy wartości „kontrolne” dla parametru a: a 1 = 0 i 2 = -1.

2) Rozwiążmy tę nierówność na każdym podzbiorze liczb rzeczywistych: (-∞; -1); (-1); (-10); (0); (0; +∞).

a)< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a = -1, wówczas nierówność ta przyjmie postać 0 x > 0 – nie ma rozwiązań;

c) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, wówczas nierówność ta ma postać 0 x > 4 – nie ma rozwiązań;

e) a > 0, z nierówności wynika, że ​​x > (a + 4)/a.

Przykład 3.

Rozwiąż nierówność |2 – |x||< a – x.

Rozwiązanie.

Budujemy wykres funkcji y = |2 – |x|| (ryc. 3) i rozważ wszystkie możliwe przypadki położenia prostej y = -x + a.

Odpowiedź: nierówność nie ma rozwiązań dla a ≤ -2;
x € (-∞; (a – 2)/2) za € (-2; 2];
x € (-∞; (a + 2)/2) dla a > 2.

Rozwiązując różne problemy, równania i nierówności z parametrami, odkrywa się znaczną liczbę technik heurystycznych, które można następnie z powodzeniem zastosować w innych gałęziach matematyki.

Problemy z parametrami odgrywają ważną rolę w kształtowaniu logicznego myślenia i kultury matematycznej. Dlatego po opanowaniu metod rozwiązywania problemów z parametrami z powodzeniem poradzisz sobie z innymi problemami.

Nadal masz pytania? Nie wiesz jak rozwiązać nierówności?
Aby uzyskać pomoc korepetytora zarejestruj się.
Pierwsza lekcja jest bezpłatna!

stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła.

Seria „Nauka rozwiązywania problemów z parametrami”

IV. Równania kwadratowe i nierówności z parametrem

IV.1. Podstawowe koncepcje

Definicja. Funkcja postaci (1), gdzie , , to dane funkcje parametru A, rozważane na przecięciu ich dziedzin definicji, będziemy nazywać funkcją kwadratową z parametrem A.

Przykłady.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Definicja. Poddziedzina definicji funkcji kwadratowej (1) z parametrem A zrozumiemy cały zbiór par wartości X I A typ ( X; A), dla każdego z nich wyrażenie nie traci znaczenia.

Ustalmy dziedziny definicji funkcji 1-10.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Jeżeli parametr przyjmuje jedną z wartości liczbowych z , to funkcja (1) przyjmie postać jednej z funkcji o współczynnikach liczbowych:

; ; ;
; ; ; ,

Gdzie k, B, C- liczby rzeczywiste.

Zwróćmy uwagę na fakt, że dla niektórych wartości parametru funkcja kwadratowa z parametrem przyjmuje postać albo funkcji kwadratowej bez parametru, albo funkcji liniowej.

Ponieważ funkcja kwadratowa z parametrem najczęściej „generuje” rodzinę funkcji kwadratowych lub liniowych o współczynnikach numerycznych, to mówiąc o wykresy funkcji kwadratowej z parametrem, będziemy mieli na myśli wiele grafów tej rodziny.

Definicja. A nazywa się równaniem postaci (1) gdzie , , są funkcjami parametru A, rozpatrywane na przecięciu ich dziedzin definicji.

W szczególności niektóre współczynniki lub wyrazy wyrazu wolnego mogą być liczbami.

Przykłady.

, (1)
, (2)
, (3)
, (4)
. (5)

Korzystając z definicji funkcji kwadratowej z parametrem, możemy podać następującą definicję równania kwadratowego z parametrem.

Definicja. Równanie kwadratowe z parametrem A nazywa się równaniem postaci , gdzie jest funkcją kwadratową z parametrem A.

Jeżeli , to równanie (1) jest kwadratowe w tradycyjnym sensie, tj. drugi stopień.
Jeśli , to równanie (1) staje się liniowe.

Dla wszystkich prawidłowych wartości parametrów A, dla którego i , korzystając ze znanych wzorów, otrzymujemy wyrażenia na pierwiastki równania (1) w funkcji parametru.

Te wartości A, w którym , należy rozpatrywać oddzielnie jako przypadki szczególne.
Na przykład równanie (5) przyjmie postać , skąd .

IV.2. Równania kwadratowe z parametrem

№1. Rozwiązać równanie.

– konsekwencja równania. Otrzymujemy: , .

W układzie współrzędnych ( och) uzupełniamy rozwiązanie. (ryc. 1)

Odpowiedź: 1. Jeśli , to .

2. Jeśli , to .

3. Jeśli , , to .

№2. Znajdź wartość parametru A, w którym równanie ma jeden pierwiastek. Jeżeli takich wartości jest kilka, w odpowiedzi zapisz ich sumę.

Równanie to sprowadza się do równoważnego układu:

Sprowadźmy to do postaci: i rozwiążmy graficznie w układzie współrzędnych ( xOa). (ryc. 2).

Równanie ma jeden pierwiastek w , i .

№3. Znajdź wszystkie wartości X tak, że dla dowolnej wartości parametru A, nienależący do przedziału (0; 2], wyrażenie nie jest równe wyrażeniu (USE-2007).

Przeformułujmy problem: „Znajdź wszystkie wartości X tak, że dla dowolnej wartości parametru równanie nie ma korzeni.”
Wyraźmy A Poprzez X:

1) Niech . Następnie . Zatem równanie ma pierwiastki. Oznacza to, że nie spełnia warunku.
2) Niech . Następnie . Skorzystajmy z układu współrzędnych ( xOa). (ryc. 3).

Warunek jest spełniony.

№4. Ile korzeni w zależności od parametru A ma równanie?

Rozwińmy moduł:

W układzie współrzędnych ( xOj) zbudujmy wykres funkcji

i kilka linii ołówka o równoległych liniach podanych w równaniu. (ryc. 4).

Odpowiedź: 1. Jeśli , to nie ma pierwiastków.

2. Jeśli , to jeden korzeń.

3. Jeśli , to są dwa pierwiastki.

IV.3. Nierówności kwadratowe z parametrem

№5. Rozwiąż nierówność .

1 sposób.

Weźmy to pod uwagę. Zatem istnieje rozwiązanie tej nierówności dla dowolnego B.(ryc. 5).

Jeśli , to przechodzimy do nierówności, której zbiór rozwiązań zostanie przedstawiony w układzie współrzędnych ( skrzynka). (ryc. 6).

Połączmy rys. 5 i 6.

A teraz zgodnie z rys. 7, przecinając go pionowymi liniami prostymi, łatwo jest uzyskać odpowiedź.

Odpowiedź: 1. Jeśli , to .
2. Jeśli , to .
3. Jeśli , to

Metoda 2.

Rozwiążmy nierówność graficznie w układzie współrzędnych ( xOb):

. (ryc. 8).

Rozważmy dwa przypadki.

1) . Wtedy nierówność przyjmie postać gdzie .
2) , następnie .

Wykres funkcji oraz część płaszczyzny zawierającą punkty, których współrzędne spełniają nierówność pokazano na rysunku 8.

1. Jeśli , to .
2. Jeśli , to . 3. Jeśli , to .

3 sposoby.

Przedstawmy teraz rozwiązanie graficzne w układzie współrzędnych ( xOj). W tym celu rozwińmy moduł:

Rozważ funkcję .

Pierwiastki trójmianu kwadratowego .

Porównajmy i .

1) , skąd .

Otrzymujemy całość. (ryc. 9)

2) , skąd . (ryc. 10).

Wtedy tj. .

3) , skąd . (ryc. 11).

Wtedy tj. .

Odpowiedź: 1. Jeśli , to .

2. Jeśli , to .
3. Jeśli , to .

№6. Znajdź wszystkie wartości parametrów A, dla którego najmniejsza wartość funkcji więcej niż 2.

Wystarczy znaleźć wszystkie wartości parametru A, dla każdego z nich nierówność jest prawdziwa dla dowolnego . Zapiszmy nierówność w postaci ., ;

Państwowa budżetowa instytucja edukacyjna

Wykształcenie średnie ogólnokształcące w regionie Samara

Szkoła nr 2 im. Kolej V. Maskina Sztuka. Klyavlino

Okręg miejski Klyavlinsky

Region Samary

« Równania

I

nierówności

z parametrami”

instruktaż

Klyavlino

Instruktaż

„Równania i nierówności z parametrami” dla uczniów klas 10–11

podręcznik ten stanowi dodatek do programu zajęć fakultatywnych „Równania i nierówności z parametrami”, który zdał egzamin zewnętrzny (rada ekspertów naukowo-metodologicznych Ministerstwa Edukacji i Nauki regionu Samara z dnia 19 grudnia 2008 r. zaleciła dla do stosowania w instytucjach edukacyjnych regionu Samara)

Autorski

Romadanova Irina Władimirowna

nauczyciel matematyki w Liceum Klyavlinskaya

Szkoła nr 2 im. V. Maskina, rejon Klyavlinsky, obwód Samara

Serbajewa Irina Aleksiejewna

Wprowadzenie………………………………………………………3-4

Równania i nierówności liniowe z parametrami……………..4-7

Równania i nierówności kwadratowe z parametrami………7-9

Równania ułamkowo-wymierne z parametrami……………..10-11

Równania i nierówności irracjonalne z parametrami… 11-13

Równania i nierówności trygonometryczne z parametrami.14-15

Równania wykładnicze i nierówności z parametrami………16-17

Równania i nierówności logarytmiczne z parametrami... 16-18

Cele ujednoliconego egzaminu państwowego………………………………………………………...18-20

Zadania do pracy samodzielnej……………………………21-28

Wstęp.

Równania i nierówności z parametrami.

Jeżeli w równaniu lub nierówności niektórym współczynnikom nie przypisuje się konkretnych wartości liczbowych, lecz oznaczono je literami, wówczas nazywa się je parametry, oraz samo równanie lub nierówność parametryczny.

Aby rozwiązać równanie lub nierówność z parametrami należy:

Wybierać specjalne znaczenie- jest to wartość parametru, w którym lub podczas przejścia, przez które zmienia się rozwiązanie równania lub nierówności.

Definiować ważne wartości– są to wartości parametru, przy których równanie lub nierówność ma sens.

Rozwiązanie równania lub nierówności z parametrami oznacza:

1) określić, przy jakich wartościach parametrów istnieją rozwiązania;

2) dla każdego dopuszczalnego układu wartości parametrów znaleźć odpowiedni zbiór rozwiązań.

Równanie z parametrem można rozwiązać metodami: analityczną lub graficzną.

Metoda analityczna polega na badaniu równania poprzez rozważenie kilku przypadków, z których żadnego nie można pominąć.

Rozwiązywanie równań i nierówności o parametrach każdego typu metodą analityczną wiąże się ze szczegółową analizą sytuacji i konsekwentnymi badaniami, podczas których pojawia się taka potrzeba „ostrożne obchodzenie się” z parametrem.

Metoda graficzna polega na skonstruowaniu wykresu równania, z którego można określić, jak zmiana parametru wpływa odpowiednio na rozwiązanie równania. Wykres pozwala czasami analitycznie sformułować warunki konieczne i wystarczające do rozwiązania problemu. Metoda rozwiązania graficznego jest szczególnie skuteczna, gdy trzeba ustalić, ile pierwiastków ma równanie w zależności od parametru, a jej niewątpliwą zaletą jest to, że wyraźnie to widać.

§ 1. Równania i nierówności liniowe.

Równanie liniowe A X = B , zapisane w formie ogólnej, można uznać za równanie z parametrami, gdzie X - nieznany , A , B - opcje. W przypadku tego równania wartością specjalną lub kontrolną parametru jest ta, przy której współczynnik nieznanego staje się zerem.

Rozwiązując równanie liniowe z parametrem, uwzględnia się przypadki, gdy parametr jest równy jego wartości specjalnej i różni się od niego.

Specjalna wartość parametru A jest wartością A = 0.

B = 0 jest specjalną wartością parametru B .

Na B ¹ 0 równanie nie ma rozwiązań.

Na B = 0 równanie będzie miało postać: 0x = 0. Rozwiązaniem tego równania jest dowolna liczba rzeczywista.

Nierówności formy aha > B I topór < B (a ≠ 0) nazywane są nierównościami liniowymi. Zbiór rozwiązań nierówności aha >B- interwał

(; +), Jeśli A > 0 , I (-;) , Jeśli A< 0 . Podobnie dla nierówności

Oh< B zbiór rozwiązań - przedział(-;), Jeśli A > 0, I (; +), Jeśli A< 0.

Przykład 1. Rozwiązać równanie topór = 5

Rozwiązanie: To jest równanie liniowe.

Jeśli a = 0, a następnie równanie 0 × x = 5 nie ma rozwiązania.

Jeśli A¹ 0, x =- rozwiązanie równania.

Odpowiedź: Na A¹ 0, x=

dla a = 0 nie ma rozwiązania.

Przykład 2. Rozwiązać równanie topór – 6 = 2a – 3x.

Rozwiązanie: To jest równanie liniowe, topór – 6 = 2a – 3x (1)

topór + 3x = 2a +6

Przepisując równanie jako (a+3)x = 2(a+3), rozważ dwa przypadki:

a= -3 I A¹ -3.

Jeśli a= -3, to dowolna liczba rzeczywista X jest pierwiastkiem równania (1). Jeśli A¹ -3 , równanie (1) ma jeden pierwiastek x = 2.

Odpowiedź: Na a = -3, x R ; Na A ¹ -3, x = 2.

Przykład 3. Przy jakich wartościach parametrów A wśród pierwiastków równania

2ah – 4kh – a 2 + 4a – 4 = 0 jest więcej korzeni 1 ?

Rozwiązanie: Rozwiążmy równanie 2ah – 4kh – a 2 + 4a – 4 = 0- równanie liniowe

2(a - 2) x = a 2 – 4a +4

2(a – 2) x = (a – 2) 2

Na a = 2 rozwiązanie równania 0x = 0 będzie dowolną liczbą, w tym jedną większą niż 1.

Na A¹ 2 x =
. Według warunku x > 1, to jest
>1 i >4.

Odpowiedź: Na A (2) U (4;∞).

Przykład 4 . Dla każdej wartości parametru A znajdź liczbę pierwiastków równania aha=8.

Rozwiązanie. topór = 8- równanie liniowe.

y = A– rodzina linii poziomych;

y = - Wykres jest hiperbolą. Zbudujmy wykresy tych funkcji.

Odpowiedź: Jeśli a =0, to równanie nie ma rozwiązań. Jeśli a ≠ 0, to równanie ma jedno rozwiązanie.

Przykład 5 . Korzystając z wykresów, dowiedz się, ile pierwiastków ma równanie:

|x| = aha – 1.

y =| x | ,

y = aha – 1– wykres jest linią prostą przechodzącą przez punkt (0;-1).

Zbudujmy wykresy tych funkcji.

Odpowiedź: Kiedy |a|>1- jeden korzeń

Na | a|≤1 – równanie nie ma pierwiastków.

Przykład 6 . Rozwiąż nierówność topór + 4 > 2x + a 2

Rozwiązanie : topór + 4 > 2x + a 2
(a – 2) x >A 2 – 4. Rozważmy trzy przypadki.

Odpowiedź. x > a + 2 Na a > 2; X<а + 2, Na A< 2; Na a=2 nie ma rozwiązań.

§ 2. Równania kwadratowe i nierówności

Równanie kwadratowe jest równaniem postaci Oh ² + B x + do = 0 , Gdzie a≠ 0,

A, B , Z - opcje.

Aby rozwiązać równania kwadratowe z parametrem, można zastosować standardowe metody rozwiązywania, korzystając z następujących wzorów:

1 ) dyskryminator równania kwadratowego: D = B ² - 4 AC , (
²- klimatyzacja)

2) wzory na pierwiastki równania kwadratowego:X 1 =
, X 2 =
,

(X 1,2 =
)

Nazywa się nierówności kwadratowe

A X 2 + B x + c > 0,A X 2 + B x + c< 0, (1), (2)

A X 2 + B x + do ≥ 0,A X 2 + B x + do ≤ 0,(3), (4)

Zbiór rozwiązań nierówności (3) otrzymujemy łącząc zbiory rozwiązań nierówności (1) i równanie , A X 2 + B x + do = 0. W podobny sposób można znaleźć zbiór rozwiązań nierówności (4).

Jeśli dyskryminator trójmianu kwadratowego A X 2 + B x + c jest mniejsza od zera, to dla a > 0 trójmian jest dodatni dla wszystkich x R.

Jeśli trójmian kwadratowy ma pierwiastki (x 1 < х 2 ), to dla > 0 jest to dodatnie na zbiorze(-; x 2 )
(X 2; +) i ujemne w przedziale

(x 1; x 2 ). Jeśli< 0, то трехчлен положителен на интервале (х 1 ; x 2 ) i ujemne dla wszystkich x (-; x 1 )
(X 2; +).

Przykład 1. Rozwiązać równanie topór² - 2 (a – 1)x – 4 = 0.

To jest równanie kwadratowe

Rozwiązanie: Specjalne znaczenie a = 0.

Na a = 0 otrzymujemy równanie liniowe 2x – 4 = 0. Ma pojedynczy korzeń x = 2.

Na a ≠ 0. Znajdźmy dyskryminator.

D = (a-1)² + 4a = (a+1)²

Jeśli a = -1, To D = 0 - jeden korzeń.

Znajdźmy pierwiastek, podstawiając a = -1.

-x² + 4x – 4= 0, to jest x² -4x + 4 = 0, znaleźliśmy to x=2.

Jeśli a ≠ - 1, To D >0 . Korzystając ze wzoru na pierwiastek otrzymujemy:x=
;

X 1 =2, x 2 = -.

Odpowiedź: Na a=0 i a= -1 równanie ma jeden pierwiastek x = 2; Na a ≠ 0 i

A ≠ - 1 równanie ma dwa pierwiastkiX 1 =2, x 2 =-.

Przykład 2. Znajdź liczbę pierwiastków tego równania x²-2x-8-a=0 w zależności od wartości parametrów A.

Rozwiązanie. Zapiszmy to równanie w postaci x²-2x-8=a

y = x²-2x-8- wykres jest parabolą;

y =a- rodzina linii poziomych.

Zbudujmy wykresy funkcji.

Odpowiedź: Kiedy A<-9 , równanie nie ma rozwiązań; gdy a=-9 równanie ma jedno rozwiązanie; Na a>-9, równanie ma dwa rozwiązania.

Przykład 3. O czym A nierówność (a – 3)x 2 – 2ax + 3a – 6 >0 obowiązuje dla wszystkich wartości x?

Rozwiązanie. Trójmian kwadratowy jest dodatni dla wszystkich wartości x jeśli

a-3 > 0 i D<0, т.е. при а, удовлетворяющих системе неравенств

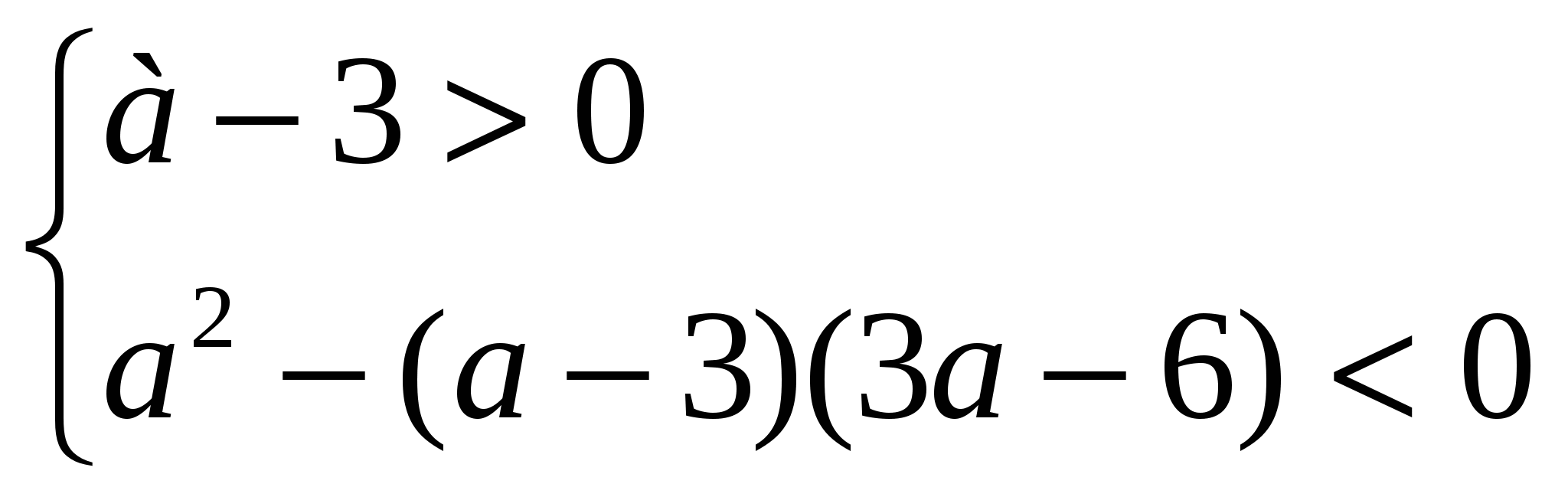
, skąd to wynikaA > 6 .

Odpowiedź.A > 6

§ 3. Ułamkowe równania wymierne z parametrem,

redukowalna do liniowej

Proces rozwiązywania równań ułamkowych odbywa się według zwykłego schematu: ułamek zastępuje się liczbą całkowitą, mnożąc obie strony równania przez wspólny mianownik jego lewej i prawej strony. Następnie rozwiązuje się całe równanie, z wyłączeniem obcych pierwiastków, to znaczy liczb, które zamieniają mianownik na zero.

W przypadku równań z parametrem problem ten jest bardziej złożony. Tutaj, aby „wyeliminować” obce pierwiastki, konieczne jest znalezienie wartości parametru, która zamienia wspólny mianownik na zero, to znaczy rozwiązać odpowiednie równania dla parametru.

Przykład 1. Rozwiązać równanie
= 0

Rozwiązanie: D.Z: x +2 ≠ 0, x ≠ -2

x – a = 0, x = a.

Odpowiedź: Na a ≠ - 2, x=a

Na a = -2 nie ma korzeni.

Przykład 2 . Rozwiązać równanie
-
=
(1)

Jest to ułamkowe równanie wymierne

Rozwiązanie: Oznaczający a = 0 jest wyjątkowy. Na a = 0 równanie nie ma sensu i dlatego nie ma pierwiastków. Jeśli a ≠ 0, wówczas po przekształceniach równanie przyjmie postać: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- równanie kwadratowe.

Znajdźmy dyskryminator = (1 – a)² - (a² - 2a – 3)= 4, znajdź pierwiastki równaniaX 1 = za + 1, x 2 = a - 3.

Przechodząc od równania (1) do równania (2), dziedzina definicji równania (1) rozszerzyła się, co mogło prowadzić do pojawienia się obcych pierwiastków. Dlatego weryfikacja jest konieczna.

Badanie. Wykluczmy ze znalezionych wartości X te, w których

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Jeśli X 1 +1=0, to jest (a+1) + 1= 0, To a= -2. Zatem,

Na a= -2 , X 1 -

Jeśli X 1 +2=0, to jest (a+1)+2=0, To a = - 3. Zatem kiedy a = - 3, x 1 - zewnętrzny pierwiastek równania. (1).

Jeśli X 2 +1=0, to jest (a – 3) + 1= 0, To a = 2. Zatem kiedy a = 2x 2 - zewnętrzny pierwiastek równania (1).

Jeśli X 2 +2=0, to jest ( a – 3) + 2 = 0, To a=1. Zatem kiedy a = 1,

X 2 - zewnętrzny pierwiastek równania (1).

Zgodnie z tym, kiedy a = - 3 dostajemy x = - 3 – 3 = -6;

Na a = - 2 x = -2 – 3= - 5;

Na a = 1x =1 + 1= 2;

Na za = 2x = 2+1 = 3.

Możesz zapisać odpowiedź.

Odpowiedź: 1) jeśli a= -3, To x= -6; 2) jeśli a= -2, To x= -5; 3) jeśli a= 0, to nie ma korzeni; 4) jeśli a= 1, To x=2; 5) jeśli a=2, To x=3; 6) jeśli a ≠ -3, a ≠ -2, a ≠ 0, a≠ 1, a ≠ 2, wtedy x 1 = za + 1, x 2 = a-3.

§4. Równania i nierówności irracjonalne

Nazywa się równania i nierówności, w których zmienna jest zawarta pod znakiem pierwiastka irracjonalny.

Rozwiązywanie równań irracjonalnych sprowadza się do przejścia od równania irracjonalnego do równania racjonalnego poprzez potęgowanie obu stron równania lub zastąpienie zmiennej. Gdy obie strony równania zostaną podniesione do równej potęgi, mogą pojawić się obce pierwiastki. Dlatego stosując tę ​​metodę, należy sprawdzić wszystkie znalezione pierwiastki, podstawiając je do pierwotnego równania, biorąc pod uwagę zmiany wartości parametrów.

Równanie postaci
=g (x) jest równoważne systemowi

Nierówność f (x) ≥ 0 wynika z równania f (x) = g 2 (x).

Rozwiązując nierówności irracjonalne, skorzystamy z następujących równoważnych przekształceń:

≤ g(x)


≥g(x)

Przykład 1. Rozwiązać równanie
= x + 1 (3)

To jest irracjonalne równanie

Rozwiązanie: Z definicji pierwiastka arytmetycznego równanie (3) jest równoważne układowi
.

Na a = 2 pierwsze równanie układu ma postać 0 x = 5, czyli nie ma rozwiązań.

Na a≠ 2x=
. Dowiedzmy się przy jakich wartościachA znaleziona wartośćX spełnia nierównośćx ≥ -1:
≥ - 1,
≥ 0,

Gdzie a ≤ Lub a > 2.

Odpowiedź: Na a≤, a > 2 x=
, Na < а ≤ 2 równanie nie ma rozwiązań.

Przykład 2. Rozwiązać równanie
= za (Załącznik 4)

Rozwiązanie. y =

y = za– rodzina linii poziomych.

Zbudujmy wykresy funkcji.

Odpowiedź: Na A<0 – nie ma rozwiązań;

Na A≥ 0 - jedno rozwiązanie.

Przykład 3 . Rozwiążmy nierówność(za+1)
<1.

Rozwiązanie. O.D.Z. x ≤ 2. Jeśli a+1 ≤0, to nierówność zachodzi dla wszystkich dopuszczalnych wartości X. Jeśli a+1>0, To

(za+1)
<1.

<

Gdzie X (2-
2

Odpowiedź. X (- ;2o godz (-;-1, X (2-
2

Na A (-1;+).

§ 5. Równania i nierówności trygonometryczne.

Oto wzory rozwiązywania najprostszych równań trygonometrycznych:

Sinx = a
x= (-1) N arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ± arccos a + 2 πn, n Z, ≤1. (2)

Jeśli >1, to równania (1) i (2) nie mają rozwiązań.

tan x = a
x= arctan a + πn, n Z, a R

ctg x = a
x = arcctg a + πn, n Z, a R

Dla każdej nierówności standardowej wskazujemy zbiór rozwiązań:

1. grzech x > a
arcsin a + 2 πn Z,

Na A <-1, X R ; Na A ≥ 1, nie ma rozwiązań.

2. . grzech x< a
π - arcsin a + 2 πnZ,

dla a≤-1 nie ma rozwiązań; dla > 1,X R

3. sałata X > A
- Arcos A + 2 πn < X < Arcos A + 2 πn , N Z ,

Na A<-1, X R ; Na A ≥ 1 , nie ma rozwiązań.

4. bo x arccos a+ 2 πnZ,

Na a≤-1 , brak rozwiązań; NaA > 1, X R

5. tan x > a, arctan a + πnZ

6.tg x< a, -π/2 + πn Z

Przykład 1. Znajdować A, dla którego to równanie ma rozwiązanie:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Rozwiązanie. Zapiszmy równanie w formie

Zos 2 X + (2 A -4) cosx +(A – 5)(a+1) =0, rozwiązując to jako kwadrat, otrzymujemy cosx = 5-A I cosx = -a-1.

Równanie cosx = 5- A ma podane rozwiązania -1≤ 5-A ≤1
4≤ A≤ 6 i równanie. cosx = - a-1 pod warunkiem -1≤ -1-A ≤ 1
-2 ≤ A ≤0.

Odpowiedź. A -2; 0
4; 6

Przykład 2. O czym Bistnieje taka nierówność
+ B> 0 obowiązuje dla wszystkich x ≠πn , N Z .

Rozwiązanie. Włóżmy A= 0. Nierówność zachodzi dla b > 0. Pokażmy teraz, że żadne b ≤0 nie spełnia warunków zadania. Rzeczywiście wystarczy umieścić x = π /2, Jeśli A <0, и х = - π /2 Na A ≥0.

Odpowiedź.b>0

§ 6. Równania wykładnicze i nierówności

1. Równanie H(X) F ( X ) = H(X) G ( X) Na H(X) > 0 jest równoważne zbiorowi dwóch systemów
I

2. W szczególnym przypadku (h (x)= A ) równanie A f(x) = A g(x) o godz A> 0, jest równoważne zbiorowi dwóch systemów

I

3. Równanie A f(x) = B , Gdzie A > 0, A ≠1, B> 0, równoważne równaniu

fa (x )= log a b . Wydarzenie A=1 są rozpatrywane oddzielnie.

Rozwiązanie najprostszych nierówności wykładniczych opiera się na własności mocy. Nierówność formyF(A X ) > 0 przy użyciu zmiany zmiennejT= A X sprowadza się do rozwiązania układu nierówności
a następnie do rozwiązania odpowiednich prostych nierówności wykładniczych.

Rozwiązując nieścisłą nierówność, konieczne jest dodanie pierwiastków odpowiedniego równania do zbioru rozwiązań ścisłej nierówności. Podobnie jak przy rozwiązywaniu równań we wszystkich przykładach zawierających wyrażenie A f (x), zakładamy A> 0. Przypadek A= 1 są rozpatrywane oddzielnie.

Przykład 1 . O czym A równanie 8x =
ma tylko pozytywne korzenie?

Rozwiązanie. Z właściwości funkcji wykładniczej o podstawie większej niż jeden wynika, że ​​x>0
8 X >1

>1

>0, skądA (1,5;4).

Odpowiedź. A (1,5;4).

Przykład 2. Rozwiąż nierówność A 2 ∙2 X > A

Rozwiązanie. Rozważmy trzy przypadki:

1. A< 0 . Ponieważ lewa strona nierówności jest dodatnia, a prawa ujemna, nierówność zachodzi dla dowolnego x R.

2. A=0. Nie ma rozwiązań.

3. A > 0 . A 2 ∙2 X > o
2 X >
x > -log 2 A

Odpowiedź. X R Na A > 0; nie ma rozwiązań A =0; X (- dziennik 2 A; +) Naa > 0 .

§ 7. Równania i nierówności logarytmiczne

Przedstawmy kilka równoważności stosowanych w rozwiązywaniu Równania i nierówności logarytmiczne.

1. Równanie log f (x) g (x) = log f (x) h (x) jest równoważne układowi

W szczególności, jeśli A >0, A Zatem ≠1

dziennik A g(x)=log A h(x)

2. Równanie dziennik A g(x)=b
g(x)=A B ( A >0, a ≠ 1, g(x) > 0).

3. Nierówność dziennik F ( X ) G (X) ≤ dziennik F ( X ) H(X) jest równoznaczne z połączeniem dwóch systemów:
I

Jeśli, b są liczbami, a > 0, a ≠1, zatem

dziennik A f(x) ≤ b

dziennik A f(x)>b

Przykład 1. Rozwiązać równanie

Rozwiązanie. Znajdźmy ODZ: x > 0, x ≠ A 4 , A > 0, A≠ 1. Przekształć równanie

dziennik x – 2 = 4 – dziennik A X
dziennik x + dziennik A X– 6 = 0, skąd dziennik A X = - 3

x = A-3 i dziennik A X = 2
x = A 2. Warunek x = A 4
A – 3 = A 4 lub A 2 = A 4 nie jest wykonywana na ODZ.

Odpowiedź: x = A-3, x = A 2 o godz A (0; 1)
(1; ).

Przykład 2 . Znajdź największą wartość A, dla którego równanie

2 dziennik -
+ A = 0 ma rozwiązania.

Rozwiązanie. Zrobimy zastępstwo
= Ti otrzymujemy równanie kwadratowe 2T 2 – T + A = 0. Rozwiązujemy, znajdujemyD = 1-8 A . Rozważmy D≥0, 1-8 A ≥0
A ≤.

Na A = równanie kwadratowe ma pierwiastekT= >0.

Odpowiedź. A =

Przykład 3 . Rozwiąż nierównośćdziennik(X 2 – 2 X + A ) > - 3

Rozwiązanie. Rozwiążmy układ nierówności

Pierwiastki trójmianów kwadratowych x 1,2 = 1 ±
ich 3,4 = 1 ±
.

Krytyczne wartości parametrów: A= 1 i A= 9.

Niech zatem X 1 i X 2 będą zbiorami rozwiązań pierwszej i drugiej nierówności

X 1
X 2 = X – rozwiązanie pierwotnej nierówności.

O godzinie 0< A <1 Х 1 = (- ;1 -
)
(1 +
; +), NaA> 1X1 = (-;+).

O godzinie 0< A < 9 Х 2 = (1 -
; 1 +
), NaA≥9 X 2 – brak rozwiązań.

Rozważmy trzy przypadki:

1. 0< A ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < A < 9 Х = (1 -
;1 +
).

3. A≥ 9 X – brak rozwiązań.

Cele egzaminu ujednoliconego stanu

Wysoki poziom C1, C2

Przykład 1. Znajdź wszystkie wartości R, dla którego równanie

R ∙ ctg 2x+2sinx+ P= 3 ma co najmniej jeden pierwiastek.

Rozwiązanie. Przekształćmy równanie

R ∙ (
- 1) + 2sinx + P= 3, sinx = t, T
, T 0.

- P+2t+ P = 3, + 2 t = 3, 3 -2 t = , 3t 2 – 2t 3 = P .

Pozwalać F(y) = 3 T 2 – 2 T 3 . Znajdźmy zbiór wartości funkcjiF(X) NA


. Na / = 6 T – 6 T 2 , 6 T - 6 T 2 = 0, T 1 =0, T 2 = 1. F(-1) = 5, F(1) = 1.

Na T
, mi(F) =
,

Na T
, mi(F) =
, to jest, kiedy T


, mi(F) =
.

Do równania 3T 2 – 2 T 3 = P (stąd podane) miało co najmniej jeden pierwiastek konieczny i wystarczającyP mi(F), to jest P
.

Odpowiedź.
.

Przykład 2.

Przy jakich wartościach parametrówA równanie dziennik
(4 X 2 – 4 A + A 2 +7) = 2 ma dokładnie jeden pierwiastek?

Rozwiązanie. Przekształćmy równanie na równoważne temu:

4x2 – 4 A + A 2 +7 = (x 2 + 2) 2.

Zauważ, że jeśli pewna liczba x jest pierwiastkiem otrzymanego równania, to liczba – x ​​jest również pierwiastkiem tego równania. Pod warunkiem, że nie jest to wykonalne, więc jedynym pierwiastkiem jest liczba 0.

Znajdziemy A.

4∙ 0 2 - 4A + A 2 +7 = (0 2 + 2) 2 ,

A 2 - 4A +7 = 4, A 2 - 4A +3 = 0, A 1 = 1, A 2 = 3.

Badanie.

1) A 1 = 1. Wtedy równanie wygląda następująco:dziennik
(4 X 2 +4) =2. Rozwiążmy to

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 jest jedynym pierwiastkiem.

2) A 2 = 3. Równanie wygląda następująco:dziennik
(4 X 2 +4) =2
x = 0 jest jedynym pierwiastkiem.

Odpowiedź. 1; 3

Wysoki poziom C4, C5

Przykład 3. Znajdź wszystkie wartości R, dla którego równanie

x 2 – ( R+ 3)x + 1= 0 ma pierwiastki całkowite i te pierwiastki są rozwiązaniami nierówności: x 3 – 7 R x 2 + 2 x 2 – 14 R x - 3x +21 R ≤ 0.

Rozwiązanie. Niech x 1, X 2 – pierwiastki całkowite równania x 2 – (R + 3)x + 1= 0. Następnie, zgodnie ze wzorem Viety, równości x 1 + x 2 = R + 3, x 1 ∙x 2 = 1. Iloczyn dwóch liczb całkowitych x 1 , X 2 może być równe jeden tylko w dwóch przypadkach: x 1 = x 2 = 1 lub x 1 = x 2 = - 1. Jeśli x 1 = x 2 = 1, zatemR + 3 = 1+1 = 2
R = - 1; jeśli x 1 = x 2 = - 1, zatemR + 3 = - 1 – 1 = - 2
R = - 5. Sprawdźmy, czy pierwiastki równania x 2 – (R + 3)x + 1= 0 w opisanych przypadkach rozwiązaniami tej nierówności. Z okazjiR = - 1, x 1 = x 2 = 1 mamy

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – prawda; z okazji R= - 5, x 1 = x 2 = - 1 mamy (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – poprawnie. Zatem warunki problemu są tylko spełnione R= - 1 i R = - 5.

Odpowiedź.R 1 = - 1 i R 2 = - 5.

Przykład 4. Znajdź wszystkie dodatnie wartości parametru A, dla którego liczba 1 należy do dziedziny definicji funkcji

Na = (A
- A
).

Zapowiedź:

MINISTERSTWO EDUKACJI REGIONU MOSKWY

Państwowa Instytucja Oświatowa NPO Szkoła Zawodowa nr 37

PROJEKT:

RÓWNANIA KWADRATOWE I NIERÓWNOŚCI Z PARAMETRAMI"

Wykonane -

Matsuk Galina Nikołajewna,

Nauczyciel matematyki, Państwowa Instytucja Oświatowa NPO

szkoła zawodowa nr 37 MO.

G. Noginsk, 2011

1. Wstęp

4. Metodyka rozwiązywania równań kwadratowych w warunkach początkowych.

6. Metodologia rozwiązywania nierówności kwadratowych z parametrami w postaci ogólnej.

7. Metodyka rozwiązywania nierówności kwadratowych w warunkach początkowych.

8. Wniosek.

9. Literatura.

1. Wstęp.

Głównym zadaniem nauczania matematyki w szkole zawodowej jest zapewnienie uczniom silnego i świadomego opanowania systemu wiedzy i umiejętności matematycznych niezbędnych w życiu codziennym i pracy, wystarczających do studiowania dyscyplin pokrewnych i kształcenia ustawicznego, a także w działalności zawodowej, która wymagają odpowiednio wysokiej kultury matematycznej.

Profilowane kształcenie matematyczne realizowane jest poprzez rozwiązywanie problemów stosowanych w zawodach związanych z obróbką metali, elektroinstalacją i obróbką drewna. Dla życia we współczesnym społeczeństwie ważne jest rozwinięcie matematycznego stylu komunikacji, który przejawia się w pewnych umiejętnościach umysłowych. Problemy z parametrami mają wartość diagnostyczną i prognostyczną. Za ich pomocą możesz sprawdzić swoją wiedzę z głównych działów matematyki elementarnej, poziom logicznego myślenia i wstępne umiejętności badawcze.

Nauczanie zadań z parametrami wymaga od uczniów dużego wysiłku umysłowego i wolicjonalnego, rozwiniętej uwagi oraz kultywowania takich cech, jak aktywność, inicjatywa twórcza i zbiorowa praca poznawcza. Zadania z parametrami ukierunkowane są na naukę podczas powtarzania ogólnego na II roku w ramach przygotowania do egzaminu państwowego oraz na III roku na zajęciach dodatkowych przygotowujących dla studentów, którzy wyrazili chęć przystąpienia do egzaminów końcowych w formie Unified State Exam .

Głównym kierunkiem modernizacji edukacji matematycznej jest rozwój mechanizmów końcowej certyfikacji poprzez wprowadzenie Jednolitego Egzaminu Państwowego. W ostatnich latach w zadaniach z matematyki wprowadzono problemy z parametrami. Zadania takie wymagane są na egzaminach wstępnych na studia. Pojawienie się takich problemów jest bardzo ważne, ponieważ za ich pomocą sprawdzają znajomość przez wnioskodawcę formuł elementarnej matematyki, metod rozwiązywania równań i nierówności, umiejętność budowania logicznego łańcucha rozumowania oraz poziom logicznego myślenia wnioskodawcy . Analiza wyników poprzednich egzaminów Unified State Exam z kilku poprzednich lat pokazuje, że absolwenci mają duże trudności z rozwiązaniem takich zadań, a wielu nawet ich nie rozpoczyna. Większość albo w ogóle nie radzi sobie z takimi zadaniami, albo dostarcza uciążliwych obliczeń. Powodem tego jest brak systemu zadań z tego tematu w podręcznikach szkolnych. W związku z tym zaistniała potrzeba przeprowadzenia w grupach absolwentów specjalnych tematów przygotowujących do egzaminów z rozwiązywania problemów z parametrami oraz problemów o charakterze stosowanym, związanych z orientacją zawodową.

Studia z tych zagadnień przeznaczone są dla studentów III roku, którzy chcą nauczyć się rozwiązywać problemy o podwyższonym stopniu złożoności w algebrze i początkach analizy. Rozwiązanie takich problemów nastręcza im znacznych trudności. Wynika to z faktu, że każde równanie lub nierówność z parametrami reprezentuje całą klasę zwykłych równań i nierówności, dla których należy uzyskać rozwiązanie.

W procesie rozwiązywania problemów z parametrami arsenał technik i metod ludzkiego myślenia obejmuje w sposób naturalny indukcję i dedukcję, uogólnianie i specyfikację, analizę, klasyfikację i systematyzację oraz analogię. Ponieważ program nauczania w szkołach zawodowych przewiduje, uwzględnione w planie zajęć, konsultacje z matematyki dla uczniów, którzy posiadają wystarczające przygotowanie matematyczne, wykazują zainteresowanie studiowanym przedmiotem i mają w dalszym ciągu zamiar dostać się na studia, wskazane jest wykorzystanie określonych godzin do rozwiązywania problemów z parametrami przygotowującymi do olimpiad, konkursów matematycznych, różnego rodzaju egzaminów, w szczególności Unified State Exam. Rozwiązanie takich problemów jest szczególnie istotne ze względów stosowanych i praktycznych, co pomoże w prowadzeniu różnych badań.

2. Cele, główne zadania, metody, technologie, wymagania wiedzy.

Cele projektu:

• Kształtowanie umiejętności i umiejętności rozwiązywania problemów z parametrami, które sprowadzają się do badania równań kwadratowych i nierówności.
• Kształtowanie zainteresowań przedmiotem, rozwijanie zdolności matematycznych, przygotowanie do Jednolitego Egzaminu Państwowego.
• Poszerzenie matematycznego zrozumienia technik i metod rozwiązywania równań i nierówności.
• Rozwój logicznego myślenia i umiejętności badawczych.
• Zaangażowanie w działalność twórczą, badawczą i edukacyjną.
• Zapewnienie warunków do samodzielnej pracy twórczej.
• Wspieranie wysiłków umysłowych i wolicjonalnych uczniów, rozwijanie uwagi, aktywności, inicjatywy twórczej i umiejętności zbiorowej pracy poznawczej.

Główne cele projektu:

• Zapewnienie uczniom możliwości realizacji swoich zainteresowań matematyką i indywidualnych możliwości jej rozwoju.
• Promuj zdobywanie wiedzy i umiejętności opartych na faktach.
• Pokazać praktyczne znaczenie zagadnień parametrycznych w obszarze badań stosowanych.
• Nauczanie metod rozwiązywania równań i nierówności standardowych i niestandardowych.
• Pogłębianie wiedzy z matematyki, zapewniając kształtowanie trwałego zainteresowania tym przedmiotem.
• Identyfikowanie i rozwijanie zdolności matematycznych uczniów.
• Zapewnij przygotowanie do wejścia na uniwersytety.
• Zapewniamy przygotowanie do zajęć zawodowych wymagających wysokiej kultury matematycznej.
• Organizowanie badań i działań projektowych, które promują rozwój umiejętności intelektualnych i komunikacyjnych.

Metody stosowane podczas zajęć:

• Wykład – przekazanie materiału teoretycznego, któremu towarzyszy rozmowa ze studentami.
• Seminaria - w celu utrwalenia materiału w zakresie omawiania teorii.
• Warsztaty – do rozwiązywania problemów matematycznych.
• Dyskusje – aby przedstawić argumenty na rzecz swoich rozwiązań.
• Różne formy zajęć grupowych i indywidualnych.
• Zajęcia badawcze, które organizowane są poprzez: pracę z materiałem dydaktycznym, przygotowanie przekazów, obronę abstraktów i prac twórczych.
• Wykłady – prezentacje z wykorzystaniem komputera i projektora.

Wykorzystane technologie:

• System szkolenia wykładowo-seminarium.
• Technologie informacyjne i komunikacyjne.
• Metoda badawcza w nauczaniu mająca na celu rozwijanie umiejętności myślenia.
• Uczenie się oparte na problemach, które zapewnia motywację do badań poprzez stawianie problemu, omówienie różnych opcji rozwiązania problemu.
• Technologia metody aktywności, która pomaga rozwijać zainteresowania poznawcze uczniów.

Wymagania dotyczące wiedzy studentów.

W wyniku poznania różnych sposobów rozwiązywania równań kwadratowych i nierówności z parametrami studenci powinni nabyć umiejętności:

• Mocno zrozum pojęcie parametru w równaniu kwadratowym i nierówności kwadratowej;
• Potrafi rozwiązywać równania kwadratowe z parametrami.
• Potrafi rozwiązywać nierówności kwadratowe za pomocą parametrów.
• Znajdź pierwiastki funkcji kwadratowej.
• Buduj wykresy funkcji kwadratowych.
• Poznaj trójmian kwadratowy.
• Stosować racjonalne metody przekształceń tożsamości.
• Skorzystaj z najczęściej stosowanych technik heurystycznych.
• Potrafić zastosować zdobytą wiedzę podczas pracy na komputerze osobistym.

Formy kontroli.

• Lekcje – samoocena i ocena towarzyszy.
• Prezentacja projektów edukacyjnych.
• Testowanie.
• Ocena – tabela.
• Zadania domowe ze zbiorów Unified State Exam z poprzednich lat.
• Papiery testowe.

3. Metodologia rozwiązywania równań kwadratowych z parametrami w postaci ogólnej.

Nie bój się problemów z parametrami. Przede wszystkim przy rozwiązywaniu równań i nierówności z parametrami należy postępować tak samo, jak przy rozwiązywaniu dowolnego równania i nierówności - jeśli to możliwe, sprowadzić podane równania lub nierówności do prostszej postaci: rozłożyć wyrażenie wymierne na czynniki, zredukować je, umieścić uwzględnić w nawiasach itp. .d. Istnieją problemy, które można podzielić na dwie duże klasy.

Pierwsza klasa obejmuje przykłady, w których konieczne jest rozwiązanie równania lub nierówności dla wszystkich możliwych wartości parametru.

Druga klasa obejmuje przykłady, w których konieczne jest znalezienie nie wszystkich możliwych rozwiązań, a jedynie tych, które spełniają dodatkowe warunki. Klasa takich problemów jest niewyczerpana.

Najbardziej zrozumiałym dla uczniów sposobem rozwiązania takich problemów jest najpierw znalezienie wszystkich rozwiązań, a następnie wybranie tych, które spełniają dodatkowe warunki.

Rozwiązując problemy z parametrami, czasami wygodniej jest konstruować wykresy na zwykłej płaszczyźnie (x, y), a czasami lepiej jest rozważać wykresy na płaszczyźnie (x, a), gdzie x jest zmienną niezależną, a „a” jest parametrem. Jest to możliwe przede wszystkim w przypadku zadania polegającego na skonstruowaniu znanych, elementarnych wykresów: linii prostych, paraboli, okręgów itp. Ponadto szkice wykresów czasami pomagają wyraźnie zobaczyć „postęp” rozwiązania.

Rozwiązując równania f (x,a) = 0 i nierówności f (x,a) › 0, musimy pamiętać, że przede wszystkim rozwiązanie rozważa się dla tych wartości parametru, przy których współczynnik jest najwyższy potęga x kwadratowego trójmianu f (x, a), zmniejszając w ten sposób stopień. Równanie kwadratowe A(a) x 2 + B(a) x + C(a) = 0 przy A(a) = 0 zamienia się w liniowe, jeśli B(a) ≠ 0, a metody rozwiązywania równań kwadratowych i liniowych są różne.

Przypomnijmy podstawowe wzory pracy z równaniami kwadratowymi.

Równanie postaci ah 2 + in + c = 0, gdzie x  R to niewiadome, a, b, c to wyrażenia zależne tylko od parametrów, a a ≠ 0 nazywa się równaniem kwadratowym, a D = b 2 – 4ac nazywa się dyskryminatorem trójmianu kwadratowego.

Jeśli D

Jeśli D > 0, to równanie ma dwa różne pierwiastki

x 1 = , x 2 = , a następnie topór 2 + in + c = a (x – x 1) (x – x 2).

Pierwiastki te powiązane są poprzez współczynniki równania za pomocą wzorów Viety

Jeśli D = 0, to równanie ma dwa zbieżne pierwiastki x 1 = x 2 = , a następnie topór 2 + in + c = a (x – x 1) 2 . W tym przypadku mówimy, że równanie ma jedno rozwiązanie.

Kiedy, tj. = 2k, pierwiastki równania kwadratowego wyznacza się ze wzoru x 1,2 = ,

Aby rozwiązać zredukowane równanie kwadratowe x 2 + piks. + q = 0

Zastosowana formuła to x 1,2 = - , a także wzory Viety

Przykłady. Rozwiąż równania:

Przykład 1. + =

Rozwiązanie:

Dla a ≠ - 1, x ≠ 2 otrzymujemy x 2 + 2ax – 3b + 4 = 0 i pierwiastki

x 1 = - za - , x 2 = -a + , istniejąca przy

A 2 + 2a – 4  0, tj. Na

Sprawdźmy teraz, czy istnieje takie, że albo x 1 lub x 2 jest równe 2. Podstaw x = 2 do równania kwadratowego i otrzymamy a = - 8.

Drugi pierwiastek w tym przypadku jest równy(zgodnie z twierdzeniem Viety) i dla a = - 8 równa się 14.

Odpowiedź: dla a = - 8 jedynym rozwiązaniem jest x = 14;

Jeśli a  (- ∞; - 8)  (- 8; - 4)  (1; + ∞) – dwa pierwiastki x 1 i x 2;

Jeśli = - jedyne rozwiązanie x =odpowiednio;

Jeśli a  (- 4; 1), to x   .

Czasami równania z wyrazami ułamkowymi są redukowane do równań kwadratowych. Rozważmy następujące równanie.

Przykład 2. - =

Rozwiązanie: Gdy a = 0 nie ma to sensu, wartość x musi spełniać warunki: x -1, x  -2. Mnożenie wszystkich wyrazów równania przez a (x + 1) (x +2) 0,

Otrzymujemy x 2 – 2(a – 1)x + a 2 – 2a – 3 = 0, równoważne temu. Jego korzenie:

x 1 = a + 1, x 2 = - 3. Z tych pierwiastków wybierzmy obce pierwiastki, tj. te, które są równe – 1 i – 2:

X 1 = a + 1 = - 1, a = - 2, ale przy a = - 2 x 2 = - 5;

X 1 = a + 1 = - 2, a = - 3, ale przy a = - 3 x 2 = - 6;

X2 = a - 3 = - 1, a = 2, ale przy a = 2 x 1 = 3;

X2 = a - 3 = - 2, a = 1, ale przy a = 1 x 1 = 2.

Odpowiedź: dla a ≠ 0, a ≠ 2, a ≠ - 3, a ≠ 1 x 1 = a + 1, x 2 = a – 3;

Gdy a = - 2 x = - 5; gdy a = - 3 x = - 6.

4. Metodyka rozwiązywania równań kwadratowych w warunkach początkowych.

Warunki parametrycznych równań kwadratowych są zróżnicowane. Na przykład trzeba znaleźć wartość parametru, dla którego pierwiastki są: dodatnie, ujemne, mają różne znaki, są większe lub mniejsze od określonej liczby itp. Aby je rozwiązać, należy skorzystać z własności pierwiastków równania kwadratowego 2 + w + do = 0.

Jeżeli D > 0, a > 0, to równanie ma dwa rzeczywiście różne pierwiastki, których znaki dla c > 0 są takie same i przeciwne do znaku współczynnika b, a dla c

Jeżeli D = 0, a > 0, to równanie ma pierwiastki rzeczywiste i równe, których znak jest przeciwny do znaku współczynnika b.

Jeżeli D 0, to równanie nie ma pierwiastków rzeczywistych.

Podobnie możemy ustalić właściwości pierwiastków równania kwadratowego dla a

1. Jeśli w równaniu kwadratowym zamienimy współczynniki a i c, otrzymamy równanie, którego pierwiastki są odwrotnością pierwiastków danego.
2. Jeśli w równaniu kwadratowym zmienimy znak współczynnika b, otrzymamy równanie, którego pierwiastki są przeciwne do pierwiastków danego.
3. Jeśli w równaniu kwadratowym współczynniki a i c mają różne znaki, to ma ono rzeczywiste pierwiastki.
4. Jeśli a > 0 i D = 0, to lewa strona równania kwadratowego jest pełnym kwadratem i odwrotnie, jeśli lewa strona równania jest pełnym kwadratem, to a > 0 i D = 0.
5. Jeśli wszystkie współczynniki równania są wymierne, a dyskryminator wyraża doskonały kwadrat, wówczas pierwiastki równania są wymierne.
6. Jeśli weźmiemy pod uwagę położenie pierwiastków względem zera, zastosujemy twierdzenie Viety.

Dobór pierwiastków trójmianu kwadratowego według warunków i położenia zer funkcji kwadratowej na osi liczbowej.

Niech f (x) = topór 2 + in + c, a  0, pierwiastki x 1 ˂ x 2,  ˂ .

	Położenie pierwiastków na osi liczbowej.	Warunek konieczny i wystarczający.
	x1,x2 	i f ( ) > 0, D  0, x 0 
	x 1, x 2 > 	i f ( ) > 0, D  0, x 0 > 
	x 1  2	i f ( )
	 1, x 2  .	i f ( ) > 0, D  0 i f ( ) > 0  0  .
	 1  2	i f ( ) > 0 i f ( )
	x 1  2 	i f ( )  ) > 0
	x 1   2	i f ( )  )

Przykład 3. Określ, przy jakich wartościach równania

x 2 – 2 (a – 1) x + 2a + 1 = 0

• nie ma korzeni:

warunek konieczny i wystarczający D

re = (a – 1) 2 – 2a – 1 = a 2 – 4a

• ma korzenie:

re  0, re = (a – 1) 2 – 2a – 1  0, a 

• ma jeden pierwiastek:

• ma dwa pierwiastki:

D > 0, tj. 

• ma pozytywne korzenie:

2(a – 1) > 0   a  4

Jeśli pytanie brzmi „ma dwa pozytywne pierwiastki”, system powinien zostać wymieniony D > 0;

• ma pierwiastki ujemne:

2(a – 1)  

• ma korzenie różnych znaków, tj. jeden jest dodatni, a drugi ujemny:

  a ;

Stan Nie trzeba go używać, wystarczy x 1x2

• ma jeden z pierwiastków równy 0:

warunkiem wystarczającym jest to, aby wolny wyraz równania był równy zeru, tj. 2a + 1 = 0, a = -1/2.

Znak drugiego pierwiastka wyznacza się albo przez podstawienie a = -1/2 do pierwotnego równania, albo, prościej, za pomocą twierdzenia Viety x 1 + x 2 = 2 (a – 1), a po podstawieniu a = -1/2 otrzymujemy x 2 = - 3, tj. dla a = -1/2 dwa pierwiastki: x 1 = 0, x 2 = - 3.

Przykład 4 . Przy jakich wartościach parametru a wykonuje się równanie

(a – 2) x 2 – 4ax +3 -2a = 0 ma unikalne rozwiązanie, które spełnia nierówność x

Rozwiązanie.

Dyskryminator 2 – (a – 2)(3 – 2a)

4a 2 – 3a + 6 + 2a 2 – 4a = 6a 2 – 7a + 6

Ponieważ 49 – 144 = - 95 a pierwszy współczynnik wynosi 6 następnie 6a 2 – 7a + 6 dla wszystkich x  R.

Wtedy x 1,2 = .

Zgodnie z warunkami problemu x2, to otrzymujemy nierówność

Mamy:

prawdziwe dla wszystkich  R.

6a 2 – 7a + 6 6a 2 – 7a - 10 2

A 1,2 = 1/12 (7  17) i 1 = 2 i 2 = - 5/6.

Dlatego -5/6

Odpowiedź: -

5. Parametr jako zmienna równoważna.

We wszystkich analizowanych zadaniachparametr traktowano jako stałą, ale nieznaną liczbę. Tymczasem z formalnego punktu widzenia parametr jest zmienną, „równą” innym występującym w przykładzie. Na przykład w tym widoku parametru postaci f (x; a) funkcje są definiowane nie za pomocą jednej (jak poprzednio), ale dwóch zmiennych. Taka interpretacja w naturalny sposób tworzy inny typ (a raczej metodę rozwiązania definiującą ten typ) problemów z parametrami. Pokażemy rozwiązanie analityczne tego typu.

Przykład 5. Na płaszczyźnie xy wskaż wszystkie punkty, przez które nie przechodzi żadna z krzywych rodziny y = x 2 – 4рх + 2р2 – 3, gdzie p jest parametrem.

Rozwiązanie: Jeśli (x 0; y 0 ) jest punktem, przez który nie przechodzi żadna z krzywych danej rodziny, wówczas współrzędne tego punktu nie spełniają pierwotnego równania. W konsekwencji problem sprowadzał się do znalezienia takiej zależności pomiędzy x i y, aby równanie podane w warunku nie miało rozwiązań. Pożądaną zależność łatwo uzyskać skupiając się nie na zmiennych x i y, ale na parametrze p. W tym przypadku pojawia się produktywny pomysł: rozważ to równanie jako kwadratowe w odniesieniu do p. Mamy

2р 2 – 4рх+ x 2 – y – 3 = 0. Dyskryminator= 8x2 + 8y + 24 musi być ujemne. Stąd otrzymujemy y ˂ - x 2 – 3 zatem wymaganym zbiorem są wszystkie punkty płaszczyzny współrzędnych leżące „pod” parabolą y = - x 2 – 3.

Odpowiedź: tak 2 – 3

6. Metodyka rozwiązywania nierówności kwadratowych za pomocą parametrów

Ogólnie.

Nierówności kwadratowe (ścisłe i nieścisłe) postaci

Dopuszczalne wartości to te wartości parametrów, dla których obowiązują a, b, c. Nierówności kwadratowe wygodnie jest rozwiązywać analitycznie lub graficznie. Ponieważ wykres funkcji kwadratowej jest parabolą, to dla a > 0 ramiona paraboli są skierowane w górę, dla

Różne pozycje paraboli f (x) = ax 2 + w + s, a  0 dla a > 0 pokazano na ryc. 1

A) b) c)

a) Jeśli f (x) > 0 i D  R;

b) Jeśli f (x) > 0 i D = 0, to x ;

c) Jeśli f (x) > 0 i D > 0, to x (-  ; x 1 )  (x 2 ; +  ).

Położenia paraboli są rozpatrywane podobnie dla a

Na przykład jeden z trzech przypadków, gdy

dla a 0 i f (x) > 0 x  (x 1; x 2);

dla a 0 i f (x)  (-  ; x 1 )  (x 2 ; +  ).

Rozważmy na przykład rozwiązanie nierówności.

Przykład 6. Rozwiąż nierówność x 2 + 2x + a > 0.

Niech D będzie dyskryminatorem trójmianu x 2 + 2x + a > 0. Dla D = 0, dla a = 1 nierówność przyjmuje postać:

(x + 1) 2 > 0

Jest to prawdą dla dowolnych rzeczywistych wartości x z wyjątkiem x = - 1.

Dla D > 0, tj. o x, trójmian x 2 + 2x + a ma dwa pierwiastki: - 1 – I

1 + a rozwiązaniem nierówności jest przedział

(-  ; - 1 – )  (- 1 + ; +  )

Nierówność tę można łatwo rozwiązać graficznie. W tym celu przedstawimy to w formie

X 2 + 2x > - a

i zbuduj wykres funkcji y = x 2 + 2x

Odcięte punktów przecięcia tego wykresu z prostą y = - a są pierwiastkami równania x 2 + 2x = - a.

Odpowiedź:

dla –a > - 1, tj. o godz, x  (-  ; x 1 )  (x 2 ;+  );

przy – a = - 1, tj. dla a = 1, x jest dowolną liczbą rzeczywistą z wyjątkiem - 1;

w – A , to znaczy dla a > 1, x jest dowolną liczbą rzeczywistą.

Przykład 7 . Rozwiąż nierówność cx 2 – 2 (s – 1)x + (s + 2)

Gdy c = 0, przyjmuje to postać: 2x + 2rozwiązaniem będzie x

Wprowadźmy zapis f(x) = cx 2 – 2 (s – 1)x + (s + 2) gdzie c ≠ 0.

W tym przypadku nierówność f(x)

Niech D będzie dyskryminatorem f(x). 0,25 D = 1 – 4 s.

Jeśli D > 0, tj. jeśli z> 0,25, wówczas znak f (x) pokrywa się ze znakiem c dla dowolnych rzeczywistych wartości x, tj. k(x)> 0 dla dowolnego x  R, co oznacza dla c > 0,25 nierówność f(x)

Jeśli D = 0, tj. c = 0,25, następnie f (x) = (0,25 x + 1,5) 2, tj. f (x)  0 dla dowolnego

X  R. Dlatego dla c = 0,25 nierówność f (x)

Rozważmy przypadek D  0). f (x) = 0 dla dwóch rzeczywistych wartości x:

x 1 = (c – 1 – ) i x 2 = (c – 1 + ).

Mogą tu wystąpić dwa przypadki:

Rozwiąż nierówność f(x)

f(x) pokrywa się ze znakiem c. Aby odpowiedzieć na to pytanie, zauważ, że - , tj. s – 1 – ˂ s – 1 + , ale ponieważ s (s – 1 – ) (s – 1 + ) i dlatego rozwiązaniem nierówności będzie:

(-  ; (s – 1 – ))  ( (s – 1 + ); +  ).

Teraz, aby rozwiązać nierówność, wystarczy wskazać te wartości c, dla których znak f (x) jest przeciwny do znaku c. Ponieważ o godzinie 0 1 2, następnie x  (x 1; x 2).

Odpowiedź: gdy c = 0 x  R;

Z  (-  ; x 2 )  (x 1 ; +  );

O godzinie 0  (x 1; x 2);

Dla c  0,25 nie ma rozwiązań.

Pogląd parametru jako zmiennej równej znajduje odzwierciedlenie w graficznych metodach rozwiązywania nierówności kwadratowych. W istocie, ponieważ parametr jest „równy prawu” zmiennej, naturalnym jest, że można go „przypisać” do własnej osi współrzędnych. W ten sposób powstaje płaszczyzna współrzędnych (x; a). Tak drobny szczegół, jak rezygnacja z tradycyjnego wyboru liter x i y do oznaczania osi, decyduje o jednej z najskuteczniejszych metod rozwiązywania problemów z parametrami.

Jest to wygodne, gdy problem dotyczy jednego parametru a i jednej zmiennej x. Sam proces rozwiązania wygląda schematycznie tak. Najpierw konstruowany jest obraz graficzny, następnie przecinając powstały wykres liniami prostymi prostopadłymi do osi parametrycznej, „usuwamy” niezbędne informacje.

Odrzucenie tradycyjnego wyboru liter x i y do oznaczenia osi wyznacza jedną z najskuteczniejszych metod rozwiązywania problemów z parametrami - „metodę dziedzinową”

1. Metodyka rozwiązywania nierówności kwadratowych w warunkach początkowych.

Rozważmy analityczne rozwiązanie nierówności kwadratowej z parametrami, których wyniki rozważamy na osi liczbowej.

Przykład 8.

Znajdź wszystkie wartości x, dla każdej z nich nierówność

(2x)a 2 +(x 2 -2x+3)a-3x≥0

jest spełniony dla dowolnej wartości należącej do przedziału [-3;0].

Rozwiązanie. Przekształćmy lewą stronę tej nierówności w następujący sposób:

(2-x)a 2 + (x 2 -2x+3)a-3x=ax 2 - a 2 x - 2ax + 2a 2 + 3a - 3x =

Topór (x - a)-2a(x - a)- 3(x-a) = (x - a)(ax- 2a - 3).

Nierówność ta będzie miała postać: (x - a) (ax - 2a - 3) ≥ 0.

Jeśli a = 0, otrzymujemy - Zx ≥ 0 x ≤ 0.

Jeśli a ≠ 0, to -3 a

Ponieważ A 0, wówczas rozwiązaniem tej nierówności będzie przedział osi liczbowej znajdujący się pomiędzy pierwiastkami równania odpowiadającymi nierówności.

Dowiedzmy się względne położenie liczb a i , biorąc pod uwagę warunek - 3 ≤ a

3 ≤a

A = -1.

Przedstawmy we wszystkich rozpatrywanych przypadkach rozwiązania tej nierówności w zależności od wartości parametrów:

Stwierdzamy, że tylko x = -1 jest rozwiązaniem tej nierówności dla dowolnej wartości parametru a .

Odpowiedź 1

8. Wniosek.

Dlaczego wybrałem projekt na temat „Opracowanie zaleceń metodologicznych dotyczących rozwiązywania równań kwadratowych i nierówności z parametrami”? Ponieważ rozwiązując dowolne równania trygonometryczne, wykładnicze, logarytmiczne, nierówności, układy, najczęściej przychodzi nam na myśl czasami liniowe, a najczęściej kwadratowe równania i nierówności. Przy rozwiązywaniu złożonych problemów z parametrami większość zadań sprowadza się, stosując przekształcenia równoważne, do wyboru rozwiązań typu: a (x – a) (x – c) > 0 (

Dokonaliśmy przeglądu teoretycznych podstaw rozwiązywania równań kwadratowych i nierówności za pomocą parametrów. Przypomnieliśmy sobie niezbędne wzory i przekształcenia, przyjrzeliśmy się różnym układom wykresów funkcji kwadratowej w zależności od wartości dyskryminatora, znaku współczynnika wiodącego, położenia pierwiastków i wierzchołków paraboli. Zidentyfikowaliśmy schemat rozwiązywania i wybierania wyników oraz opracowaliśmy tabelę.

Projekt demonstruje analityczne i graficzne metody rozwiązywania równań i nierówności kwadratowych. Uczniowie szkoły zawodowej potrzebują wizualnej percepcji materiału, aby lepiej go przyswoić. Pokazano, jak można zmienić zmienną x i przyjąć parametr jako wartość równą.

Aby dobrze zrozumieć ten temat, rozważono rozwiązanie 8 problemów z parametrami, 1 – 2 dla każdej sekcji. W przykładzie nr 1 rozważana jest liczba rozwiązań dla różnych wartości parametru, w przykładzie nr 3 rozwiązanie równania kwadratowego jest analizowane w różnych warunkach początkowych. Wykonano ilustrację graficzną rozwiązywania nierówności kwadratowych. W przykładzie nr 5 zastosowano metodę zamiany parametru na wartość równą. Projekt obejmuje rozważenie przykładu nr 8 z zadań zawartych w części C dotyczącego intensywnego przygotowania do zdania Unified State Exam.

Aby zapewnić wysokiej jakości szkolenie studentów w rozwiązywaniu problemów z parametrami, zaleca się pełne wykorzystanie technologii multimedialnych, a mianowicie: korzystanie z prezentacji do wykładów, elektronicznych podręczników i książek oraz własnych opracowań z biblioteki multimediów. Lekcje binarne z matematyki + informatyki są bardzo efektywne. Internet jest niezastąpionym pomocnikiem nauczycieli i uczniów. Do prezentacji wymagane są obiekty importowane z istniejących zasobów edukacyjnych. Najwygodniejszym i najbardziej akceptowalnym w obsłudze jest centrum „Korzystanie z pakietu Microsoft Office w szkole”.

Opracowanie zaleceń metodycznych na ten temat ułatwi pracę młodym nauczycielom, którzy przychodzą do pracy w szkole, uzupełni portfolio nauczyciela, posłuży za wzór do przedmiotów specjalnych, a przykładowe rozwiązania pomogą uczniom radzić sobie ze złożonymi zadaniami.

9. Literatura.

1. Gornshtein P.I., Polonsky V.B., Yakir M.S. Problemy z parametrami. „Ilexa”, „Gymnasium”, Moskwa - Charków, 2002.

2. Balayan E.N. Zbiór problemów z matematyki przygotowujących do jednolitego egzaminu państwowego i olimpiad. 9-11 klas. „Feniks”, Rostów nad Donem, 2010.

3. Yastrebinetsky G.A. Problemy z parametrami. M., „Oświecenie”, 1986.

4. Kolesnikova S.I. Matematyka. Rozwiązywanie złożonych problemów jednolitego egzaminu państwowego. M. „IRIS – prasa”, 2005.

5. Rodionov E.M., Sinyakova S.L. Matematyka. Poradnik dla kandydatów na uczelnie. Centrum szkoleniowe „Orientir” MSTU im. NE Bauman, M., 2004.

6. Skanavi M.I. Zbiór problemów matematycznych dla osób rozpoczynających naukę na uniwersytetach: w 2 książkach. Księga 1, M., 2009.