Matematyczne oczekiwanie zmiennej losowej. Podstawy teorii prawdopodobieństwa
2. Podstawy teorii prawdopodobieństwa
Wartość oczekiwana
Rozważ zmienną losową o wartościach liczbowych. Często warto powiązać z tą funkcją liczbę - jej „wartość średnią” lub, jak mówią, „wartość średnią”, „wskaźnik tendencji centralnej”. Z wielu powodów, z których niektóre staną się jasne w dalszej części, często używa się średniej jako średniej.
Definicja 3. Matematyczne oczekiwanie zmiennej losowej X nazywany numerem
te. matematyczne oczekiwanie zmiennej losowej jest ważoną sumą wartości zmiennej losowej o wagach równych prawdopodobieństwu odpowiednich zdarzeń elementarnych.
Przykład 6 Obliczmy matematyczne oczekiwanie liczby, która wypadnie na górną ściankę kostki. Bezpośrednio z definicji 3 wynika, że
Oświadczenie 2. Niech zmienna losowa X przyjmuje wartości x 1, x 2, ..., xM. Potem równość
![]() (5)
(5)
te. Oczekiwanie matematyczne zmiennej losowej to ważona suma wartości zmiennej losowej o wagach równych prawdopodobieństwu, że zmienna losowa przyjmie określone wartości.
W przeciwieństwie do (4), gdzie sumowanie odbywa się bezpośrednio po zdarzeniach elementarnych, zdarzenie losowe może składać się z kilku zdarzeń elementarnych.
Czasami za definicję oczekiwania matematycznego przyjmuje się relację (5). Jednakże korzystając z Definicji 3, jak pokazano poniżej, łatwiej jest ustalić właściwości oczekiwań matematycznych potrzebnych do budowy probabilistycznych modeli zjawisk rzeczywistych, niż korzystając z zależności (5).
Aby udowodnić zależność (5), grupujemy w (4) terminy o tych samych wartościach zmiennej losowej :

Ponieważ stały współczynnik można odjąć od znaku sumy, zatem
Z definicji prawdopodobieństwa zdarzenia
![]()
Za pomocą dwóch ostatnich relacji otrzymujemy pożądane:

Pojęcie oczekiwań matematycznych w teorii probabilistyczno-statystycznej odpowiada pojęciu środka ciężkości w mechanice. Ujmijmy to w kropki x 1, x 2, ..., xM na numerycznej osi masy P(X= X 1 ), P(X= X 2 ),…, P(X= x m) odpowiednio. Wówczas z równości (5) wynika, że środek ciężkości tego układu punktów materialnych pokrywa się z oczekiwaniem matematycznym, co świadczy o naturalności Definicji 3.
Oświadczenie 3. Pozwalać X- wartość losowa, M(X) jest jego matematycznym oczekiwaniem, A- jakiś numer. Następnie
1) M(a)=a; 2) M(X-M(X))=0; 3M[(X- A) 2 ]= M[(X- M(X)) 2 ]+(A- M(X)) 2 .
Aby to udowodnić, najpierw rozważymy zmienną losową, która jest stała, tj. funkcja odwzorowuje przestrzeń zdarzeń elementarnych w pojedynczy punkt A. Ponieważ stały współczynnik można odjąć od znaku sumy, zatem
Jeśli każdy wyraz sumy zostanie podzielony na dwa składniki, wówczas całą sumę również podzieli się na dwie sumy, z których pierwsza składa się z pierwszych składników, a druga z drugiego. Dlatego matematyczne oczekiwanie sumy dwóch zmiennych losowych X+Y, zdefiniowane na tej samej przestrzeni zdarzeń elementarnych, jest równe sumie oczekiwań matematycznych M(X) I M(U) te zmienne losowe:
M(X+Y) = M(X) + M(Y).
I dlatego M(X-M(X)) = M(X) - M(M(X)). Jak pokazane powyżej, M(M(X)) = M(X). Stąd, M(X-M(X)) = M(X) - M(X) = 0.
Ponieważ (X - a) 2 = ((X – M(X)) + (M(X) - A)} 2 = (X - M(X)) 2 + 2(X - M(X))(M(X) - A) + (M(X) – A) 2 , To M[(X - a) 2] =M(X - M(X)) 2 + M{2(X - M(X))(M(X) - A)} + M[(M(X) – A) 2 ]. Uprośćmy ostatnią równość. Jak pokazano na początku dowodu Twierdzenia 3, oczekiwanie na stałą jest samą stałą, a zatem M[(M(X) – A) 2 ] = (M(X) – A) 2 . Ponieważ stały współczynnik można odjąć od znaku sumy, zatem M{2(X - M(X))(M(X) - A)} = 2(M(X) - A)M(X - M(X)). Prawa strona ostatniej równości wynosi 0, ponieważ, jak pokazano powyżej, M(X-M(X))=0. Stąd, M[(X- A) 2 ]= M[(X- M(X)) 2 ]+(A- M(X)) 2 , co należało udowodnić.
Z tego co powiedziano wynika, że M[(X- A) 2 ] osiąga minimum A równy M[(X- M(X)) 2 ], Na a = M(X), ponieważ drugi wyraz w równości 3) jest zawsze nieujemny i wynosi 0 tylko dla określonej wartości A.
Oświadczenie 4. Niech zmienna losowa X przyjmuje wartości x 1, x 2, ..., xM, oraz f jest pewną funkcją argumentu numerycznego. Następnie
![]()
Aby to udowodnić, zgrupujmy po prawej stronie równości (4), która wyznacza oczekiwanie matematyczne, wyrazy o tych samych wartościach:

Korzystając z faktu, że ze znaku sumy można odjąć stały współczynnik i wyznaczając prawdopodobieństwo zdarzenia losowego (2), otrzymujemy
co było do okazania
Oświadczenie 5. Pozwalać X I Na są zmiennymi losowymi zdefiniowanymi na tej samej przestrzeni zdarzeń elementarnych, A I B- kilka liczb. Następnie M(topór+ przez)= jestem(X)+ bM(Y).
Korzystając z definicji oczekiwania matematycznego i właściwości symbolu sumowania, otrzymujemy łańcuch równości:

Wymagane zostało udowodnione.
Powyższe pokazuje, jak oczekiwanie matematyczne zależy od przejścia do innego początku i do innej jednostki miary (przejście Y=topór+B), a także do funkcji zmiennych losowych. Uzyskane wyniki są stale wykorzystywane w analizie techniczno-ekonomicznej, przy ocenie działalności finansowo-ekonomicznej przedsiębiorstwa, przy przejściu z jednej waluty na drugą w zagranicznych rozliczeniach gospodarczych, w dokumentacji regulacyjnej i technicznej itp. Uwzględnione wyniki pozwalają na wykorzystanie te same wzory obliczeniowe dla różnych parametrów, skali i przesunięcia.
| Poprzedni |
Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i ich prawdopodobieństw.
Niech zmienna losowa może przyjmować tylko takie prawdopodobieństwa, które są odpowiednio równe.Wtedy matematyczne oczekiwanie zmiennej losowej jest określone przez równość
Jeśli dyskretna zmienna losowa przyjmuje przeliczalny zbiór możliwych wartości, to
Co więcej, oczekiwanie matematyczne istnieje, jeśli szereg po prawej stronie równości jest zbieżny bezwzględnie.
Komentarz. Z definicji wynika, że oczekiwanie matematyczne dyskretnej zmiennej losowej jest zmienną nielosową (stałą).
Definicja oczekiwań matematycznych w przypadku ogólnym
Zdefiniujmy matematyczne oczekiwanie zmiennej losowej, której rozkład niekoniecznie jest dyskretny. Zacznijmy od przypadku nieujemnych zmiennych losowych. Chodzić będzie o to, aby takie zmienne losowe aproksymować za pomocą dyskretnych, dla których zostało już określone oczekiwanie matematyczne, i wyznaczać oczekiwanie matematyczne na poziomie granicy oczekiwań matematycznych aproksymujących je dyskretnych zmiennych losowych. Swoją drogą jest to bardzo przydatna ogólna koncepcja, która polega na tym, że najpierw wyznacza się jakąś cechę dla obiektów prostych, a następnie dla obiektów bardziej złożonych wyznacza się ją poprzez aproksymację ich prostszymi.
Lemat 1. Niech istnieje dowolna nieujemna zmienna losowa. Następnie istnieje ciąg dyskretnych zmiennych losowych taki, że

Dowód. Podzielmy półoś na równe odcinki długości i zdefiniujmy
Następnie właściwości 1 i 2 wynikają łatwo z definicji zmiennej losowej, oraz
Lemat 2. Niech będzie nieujemną zmienną losową i dwoma ciągami dyskretnych zmiennych losowych o właściwościach 1-3 z Lematu 1. Następnie
Dowód. Należy zauważyć, że w przypadku nieujemnych zmiennych losowych dopuszczamy
Z własności 3 łatwo zauważyć, że istnieje taki ciąg liczb dodatnich, że
Stąd wynika
Korzystając z właściwości oczekiwań matematycznych dla dyskretnych zmiennych losowych, otrzymujemy
Przechodząc do granicy, otrzymujemy twierdzenie Lematu 2.
Definicja 1. Niech będzie nieujemną zmienną losową, będzie ciągiem dyskretnych zmiennych losowych o właściwościach 1-3 z Lematu 1. Oczekiwaniem matematycznym zmiennej losowej jest liczba
Lemat 2 gwarantuje, że nie zależy to od wyboru ciągu aproksymującego.
Niech teraz będzie dowolną zmienną losową. Zdefiniujmy


Z definicji i łatwo to wynika

Definicja 2. Matematycznym oczekiwaniem dowolnej zmiennej losowej jest liczba
Jeśli przynajmniej jedna z liczb po prawej stronie tej równości jest skończona.
Właściwości oczekiwań
Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe samej stałej:
Dowód. Rozważymy stałą jako dyskretną zmienną losową, która ma jedną możliwą wartość i przyjmuje ją z prawdopodobieństwem, dlatego
Uwaga 1. Iloczyn wartości stałej przez dyskretną zmienną losową definiujemy jako dyskretną zmienną losową, której możliwe wartości są równe iloczynom stałej przez możliwe wartości; prawdopodobieństwa możliwych wartości są równe prawdopodobieństwom odpowiednich możliwych wartości.Na przykład, jeśli prawdopodobieństwo możliwej wartości jest równe, wówczas prawdopodobieństwo, że wartość przyjmie wartość, jest również równe
Właściwość 2. Ze znaku oczekiwania można wyjąć stały współczynnik:
Dowód. Niech zmienna losowa będzie dana przez prawo rozkładu prawdopodobieństwa:
Biorąc pod uwagę uwagę 1, piszemy prawo rozkładu zmiennej losowej
Uwaga 2. Przed przejściem do następnej właściwości wskazujemy, że dwie zmienne losowe nazywane są niezależnymi, jeśli prawo rozkładu jednej z nich nie zależy od tego, jakie możliwe wartości przyjęła druga zmienna. W przeciwnym razie zmienne losowe są zależne. Kilka zmiennych losowych nazywa się wzajemnie niezależnymi, jeśli prawa rozkładu dowolnej ich liczby nie zależą od tego, jakie możliwe wartości przyjęły inne zmienne.
Uwaga 3. Definiujemy iloczyn niezależnych zmiennych losowych i jako zmienną losową, której możliwe wartości są równe iloczynom każdej możliwej wartości przez każdą możliwą wartość prawdopodobieństw możliwych wartości iloczynu są równe do iloczynów prawdopodobieństw możliwych wartości czynników. Na przykład, jeśli prawdopodobieństwo możliwej wartości wynosi, prawdopodobieństwo możliwej wartości wynosi wówczas prawdopodobieństwo możliwej wartości wynosi
Własność 3. Oczekiwanie matematyczne iloczynu dwóch niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
Dowód. Niech niezależne zmienne losowe będą dane według własnych praw rozkładu prawdopodobieństwa:
Uzupełnijmy wszystkie wartości, jakie może przyjąć zmienna losowa.W tym celu mnożymy wszystkie możliwe wartości przez każdą możliwą wartość; w rezultacie otrzymujemy i biorąc pod uwagę uwagę 3, piszemy prawo podziału zakładając dla uproszczenia, że wszystkie możliwe wartości produktu są różne (jeśli tak nie jest, to dowód przeprowadza się analogicznie):
Oczekiwanie matematyczne jest równe sumie iloczynów wszystkich możliwych wartości i ich prawdopodobieństw:
Konsekwencja. Oczekiwanie matematyczne iloczynu kilku wzajemnie niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych.
Właściwość 4. Oczekiwanie matematyczne sumy dwóch zmiennych losowych jest równe sumie oczekiwań matematycznych wyrazów:
Dowód. Niech zmienne losowe i będą podane przez następujące prawa dystrybucji:
Skomponuj wszystkie możliwe wartości ilości. Aby to zrobić, dodaj każdą możliwą wartość do każdej możliwej wartości; otrzymujemy Załóżmy dla uproszczenia, że te możliwe wartości są różne (jeśli tak nie jest, to dowód przeprowadzamy w podobny sposób) i oznaczamy ich prawdopodobieństwa przez i odpowiednio
Matematyczne oczekiwanie wartości jest równe sumie iloczynów możliwych wartości według ich prawdopodobieństw:
Udowodnimy, że Zdarzenie polegające na przyjęciu wartości (prawdopodobieństwo tego zdarzenia jest równe) pociąga za sobą zdarzenie polegające na przyjęciu wartości lub (prawdopodobieństwo tego zdarzenia jest równe na mocy twierdzenia o dodawaniu) i odwrotnie. Stąd wynika, że równości
Podstawiając odpowiednie części tych równości do relacji (*), otrzymujemy
lub wreszcie
Dyspersja i odchylenie standardowe
W praktyce często wymagane jest oszacowanie rozrzutu możliwych wartości zmiennej losowej wokół jej wartości średniej. Na przykład w artylerii ważne jest, aby wiedzieć, jak blisko pociski spadną blisko celu, który ma zostać trafiony.
Na pierwszy rzut oka może się wydawać, że najłatwiejszym sposobem oszacowania rozproszenia jest obliczenie wszystkich możliwych wartości odchylenia zmiennej losowej, a następnie znalezienie ich wartości średniej. Ścieżka ta jednak nic nie da, gdyż średnia wartość odchylenia, tj. dla dowolnej zmiennej losowej wynosi zero. Właściwość tę tłumaczy się faktem, że niektóre możliwe odchylenia są dodatnie, a inne ujemne; w wyniku ich wzajemnego zniesienia średnia wartość odchylenia wynosi zero. Rozważania te wskazują na celowość zastąpienia możliwych odchyleń ich wartościami bezwzględnymi lub kwadratami. Tak to robią w praktyce. Co prawda, w przypadku zastąpienia ewentualnych odchyleń ich wartościami bezwzględnymi, należy operować wartościami bezwzględnymi, co czasami prowadzi do poważnych trudności. Dlatego najczęściej idą w drugą stronę, tj. obliczyć średnią wartość kwadratu odchylenia, co nazywa się wariancją.
Pojawią się także zadania do samodzielnego rozwiązania, do których będzie można zobaczyć odpowiedzi.
Oczekiwanie matematyczne i wariancja to najczęściej stosowane cechy liczbowe zmiennej losowej. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. Oczekiwanie matematyczne jest często określane po prostu jako średnia. zmienna losowa. Rozproszenie zmiennej losowej - charakterystyka rozproszenia, rozproszenie zmiennej losowej wokół jego matematycznych oczekiwań.
W wielu praktycznych problemach pełny, wyczerpujący opis zmiennej losowej – prawo rozkładu – albo nie jest możliwy do uzyskania, albo nie jest w ogóle potrzebny. W takich przypadkach ograniczają się one do przybliżonego opisu zmiennej losowej za pomocą charakterystyk numerycznych.
Oczekiwanie matematyczne dyskretnej zmiennej losowej
Przejdźmy do koncepcji oczekiwań matematycznych. Niech masa jakiejś substancji zostanie rozłożona pomiędzy punktami osi x X1 , X 2 , ..., X N. Co więcej, każdemu punktowi materialnemu odpowiada masa z prawdopodobieństwem P1 , P 2 , ..., P N. Wymagany jest wybór jednego punktu na osi x, który charakteryzuje położenie całego układu punktów materialnych, biorąc pod uwagę ich masy. Naturalnym jest, że za taki punkt przyjmuje się środek masy układu punktów materialnych. Jest to średnia ważona zmiennej losowej X, w którym odcięta każdego punktu XI wchodzi z „wagą” równą odpowiedniemu prawdopodobieństwu. Otrzymana w ten sposób średnia wartość zmiennej losowej X nazywa się jego oczekiwaniem matematycznym.
Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i prawdopodobieństw tych wartości:
Przykład 1 Zorganizował loterię, w której wygrywają obie strony. Wygranych jest 1000, z czego 400 po 10 rubli. 300 - 20 rubli za sztukę 200 - 100 rubli za sztukę. i 100 - 200 rubli za sztukę. Jaka jest średnia wygrana osoby, która kupi jeden los?
Rozwiązanie. Średnią wygraną znajdziemy, jeśli łączna kwota wygranych równa 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rubli zostanie podzielona przez 1000 (całkowita kwota wygranych). Następnie otrzymujemy 50000/1000 = 50 rubli. Ale wyrażenie służące do obliczania średniego zysku można również przedstawić w następującej formie:
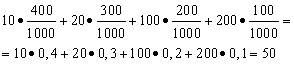
Z drugiej strony w tych warunkach kwota wygranych jest zmienną losową, która może przyjmować wartości 10, 20, 100 i 200 rubli. z prawdopodobieństwem równym odpowiednio 0,4; 0,3; 0,2; 0,1. Zatem oczekiwana średnia wypłata jest równa sumie iloczynów wielkości wypłat i prawdopodobieństwa ich otrzymania.
Przykład 2 Wydawca podjął decyzję o wydaniu nowej książki. Zamierza sprzedać książkę za 280 rubli, z czego 200 otrzyma jemu, 50 księgarni, a 30 autorowi. Tabela podaje informacje o koszcie wydania książki i prawdopodobieństwie sprzedaży określonej liczby egzemplarzy książki.
Znajdź oczekiwany zysk wydawcy.
Rozwiązanie. Zmienna losowa „zysk” jest równa różnicy między przychodem ze sprzedaży a kosztem kosztów. Na przykład, jeśli sprzeda się 500 egzemplarzy książki, dochód ze sprzedaży wynosi 200 * 500 = 100 000, a koszt publikacji to 225 000 rubli. Tym samym wydawcy grozi strata w wysokości 125 000 rubli. Poniższa tabela podsumowuje oczekiwane wartości zmiennej losowej – zysk:
| Numer | Zysk XI | Prawdopodobieństwo PI | XI P I |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Całkowity: | 1,00 | 25000 |
Otrzymujemy w ten sposób matematyczne oczekiwanie zysku wydawcy:
![]() .
.
Przykład 3 Szansa na trafienie jednym strzałem P= 0,2. Określ zużycie pocisków, które zapewniają matematyczne oczekiwanie liczby trafień równe 5.
Rozwiązanie. Z tego samego wzoru oczekiwań, którego używaliśmy do tej pory, wyrażamy X- spożycie muszli:
![]() .
.
Przykład 4 Określ oczekiwanie matematyczne zmiennej losowej X liczba trafień trzema strzałami, jeżeli prawdopodobieństwo trafienia przy każdym strzale P = 0,4 .
Wskazówka: znajdź prawdopodobieństwo wartości zmiennej losowej według Wzór Bernoulliego .
Właściwości oczekiwań
Rozważmy właściwości oczekiwań matematycznych.
Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe tej stałej:
Własność 2. Ze znaku oczekiwania można wyjąć współczynnik stały:
Własność 3. Oczekiwanie matematyczne sumy (różnicy) zmiennych losowych jest równe sumie (różnicy) ich oczekiwań matematycznych:
Właściwość 4. Oczekiwanie matematyczne iloczynu zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
Własność 5. Jeśli wszystkie wartości zmiennej losowej X zmniejszyć (zwiększyć) o tę samą liczbę Z, to jego oczekiwanie matematyczne zmniejszy się (zwiększy) o tę samą liczbę:
![]()
Kiedy nie można ograniczać się jedynie do oczekiwań matematycznych
W większości przypadków jedynie oczekiwanie matematyczne nie jest w stanie odpowiednio scharakteryzować zmiennej losowej.
Niech zmienne losowe X I Y wynikają z następujących praw dystrybucji:
| Oznaczający X | Prawdopodobieństwo |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Oznaczający Y | Prawdopodobieństwo |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Oczekiwania matematyczne tych wielkości są takie same – równe zeru:
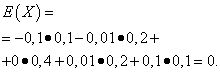

Różni się jednak ich dystrybucja. Losowa wartość X może przyjmować tylko wartości niewiele różniące się od oczekiwań matematycznych i zmiennej losowej Y może przyjmować wartości znacznie odbiegające od oczekiwań matematycznych. Podobny przykład: średnia płaca nie pozwala ocenić proporcji wysoko i nisko opłacanych pracowników. Innymi słowy, na podstawie oczekiwań matematycznych nie można ocenić, jakie odchylenia od nich, przynajmniej średnio, są możliwe. Aby to zrobić, musisz znaleźć wariancję zmiennej losowej.
Rozproszenie dyskretnej zmiennej losowej
dyspersja Dyskretna zmienna losowa X nazywa się oczekiwaniem matematycznym kwadratu jego odchylenia od oczekiwania matematycznego:

Odchylenie standardowe zmiennej losowej X jest wartością arytmetyczną pierwiastka kwadratowego z jego wariancji:
![]() .
.
Przykład 5 Obliczanie wariancji i odchyleń standardowych zmiennych losowych X I Y, których prawa dystrybucji podano w tabelach powyżej.
Rozwiązanie. Matematyczne oczekiwania zmiennych losowych X I Y, jak stwierdzono powyżej, są równe zeru. Zgodnie ze wzorem dyspersji dla mi(X)=mi(y)=0 otrzymujemy:
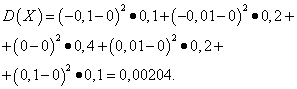
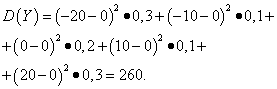
Następnie odchylenia standardowe zmiennych losowych X I Y stanowić
![]() .
.
Zatem przy tych samych oczekiwaniach matematycznych wariancja zmiennej losowej X bardzo mały i przypadkowy Y- istotne. Jest to konsekwencja różnicy w ich rozmieszczeniu.
Przykład 6 Inwestor posiada 4 alternatywne projekty inwestycyjne. W tabeli zestawiono dane dotyczące oczekiwanego zysku w tych projektach z odpowiednim prawdopodobieństwem.
| Projekt 1 | Projekt 2 | Projekt 3 | Projekt 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Znajdź dla każdej alternatywy matematyczne oczekiwanie, wariancję i odchylenie standardowe.
Rozwiązanie. Pokażmy, jak te wielkości są obliczane dla 3. alternatywy:
Tabela podsumowuje znalezione wartości dla wszystkich alternatyw.
Wszystkie alternatywy mają takie same oczekiwania matematyczne. Oznacza to, że w dłuższej perspektywie wszyscy mają takie same dochody. Odchylenie standardowe można interpretować jako miarę ryzyka – im większe, tym większe ryzyko inwestycji. Inwestor, który nie chce dużego ryzyka, wybierze projekt 1, ponieważ ma najmniejsze odchylenie standardowe (0). Jeżeli inwestor preferuje ryzyko i wysokie zyski w krótkim czasie, to wybierze projekt o największym odchyleniu standardowym – projekt 4.
Właściwości dyspersji
Przedstawiamy właściwości dyspersji.
Właściwość 1. Rozrzut wartości stałej wynosi zero:
Własność 2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu:
![]() .
.
Własność 3. Wariancja zmiennej losowej jest równa matematycznemu oczekiwaniu kwadratu tej wartości, od którego odejmuje się kwadrat matematycznego oczekiwania samej wartości:
![]() ,
,
Gdzie ![]() .
.
Właściwość 4. Wariancja sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wariancji:
Przykład 7 Wiadomo, że dyskretna zmienna losowa X przyjmuje tylko dwie wartości: −3 i 7. Ponadto znane jest oczekiwanie matematyczne: mi(X) = 4 . Znajdź wariancję dyskretnej zmiennej losowej.
Rozwiązanie. Oznacz przez P prawdopodobieństwo, z jakim zmienna losowa przyjmuje wartość X1 = −3 . Następnie prawdopodobieństwo wartości X2 = 7 będzie 1- P. Wyprowadźmy równanie oczekiwań matematycznych:
mi(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,
gdzie otrzymujemy prawdopodobieństwa: P= 0,3 i 1 − P = 0,7 .
Prawo rozkładu zmiennej losowej:
| X | −3 | 7 |
| P | 0,3 | 0,7 |
Wariancję tej zmiennej losowej obliczamy korzystając ze wzoru z właściwości 3 wariancji:
D(X) = 2,7 + 34,3 − 16 = 21 .
Znajdź samodzielnie matematyczne oczekiwanie zmiennej losowej, a następnie zobacz rozwiązanie
Przykład 8 Dyskretna zmienna losowa X przyjmuje tylko dwie wartości. Przyjmuje większą wartość 3 z prawdopodobieństwem 0,4. Ponadto znana jest wariancja zmiennej losowej D(X) = 6 . Znajdź matematyczne oczekiwanie zmiennej losowej.
Przykład 9 W urnie znajduje się 6 kul białych i 4 czarne. Z urny wyjmujemy 3 kule. Liczba białych kul wśród wylosowanych kul jest dyskretną zmienną losową X. Znajdź matematyczne oczekiwanie i wariancję tej zmiennej losowej.
Rozwiązanie. Losowa wartość X może przyjmować wartości 0, 1, 2, 3. Z odpowiednich prawdopodobieństw można obliczyć zasada mnożenia prawdopodobieństw. Prawo rozkładu zmiennej losowej:
| X | 0 | 1 | 2 | 3 |
| P | 1/30 | 3/10 | 1/2 | 1/6 |
Stąd matematyczne oczekiwanie tej zmiennej losowej:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Wariancja danej zmiennej losowej wynosi:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Matematyczne oczekiwanie i rozproszenie ciągłej zmiennej losowej
W przypadku ciągłej zmiennej losowej mechaniczna interpretacja oczekiwań matematycznych zachowa to samo znaczenie: środek masy jednostki masy rozłożonej w sposób ciągły na osi x z gęstością F(X). W przeciwieństwie do dyskretnej zmiennej losowej, dla której argumentem jest funkcja XI zmienia się nagle, w przypadku ciągłej zmiennej losowej argument zmienia się w sposób ciągły. Jednak matematyczne oczekiwanie ciągłej zmiennej losowej jest również powiązane z jej średnią wartością.
Aby znaleźć matematyczne oczekiwanie i wariancję ciągłej zmiennej losowej, należy znaleźć całki oznaczone . Jeśli podana jest funkcja gęstości ciągłej zmiennej losowej, to wchodzi ona bezpośrednio do całki. Jeśli podana jest funkcja rozkładu prawdopodobieństwa, to różniczkując ją, musisz znaleźć funkcję gęstości.
Nazywa się ją średnią arytmetyczną wszystkich możliwych wartości ciągłej zmiennej losowej oczekiwanie matematyczne, oznaczone lub .
Rozwiązanie:
6.1.2 Właściwości oczekiwań
1. Matematyczne oczekiwanie na stałą wartość jest równe samej stałej.
2. Ze znaku oczekiwania można wyjąć stały współczynnik. ![]()
3. Oczekiwanie matematyczne iloczynu dwóch niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych.
Właściwość ta obowiązuje dla dowolnej liczby zmiennych losowych.
4. Oczekiwanie matematyczne sumy dwóch zmiennych losowych jest równe sumie oczekiwań matematycznych wyrazów.
Właściwość ta jest również prawdziwa dla dowolnej liczby zmiennych losowych.
Przykład: M(X) = 5, MÓJ)= 2. Znajdź matematyczne oczekiwanie zmiennej losowej Z, stosując właściwości oczekiwań matematycznych, jeśli o tym wiadomo Z=2X + 3Y.
Rozwiązanie: M(Z) = M(2X + 3Y) = M(2X) + M(3Y) = 2M(X) + 3M(Y) = 2∙5+3∙2 =
1) matematyczne oczekiwanie sumy jest równe sumie oczekiwań matematycznych
2) ze znaku oczekiwania można usunąć stały współczynnik
Przeprowadźmy n niezależnych prób, a prawdopodobieństwo zajścia zdarzenia A będzie równe p. Wtedy zachodzi następujące twierdzenie:
Twierdzenie. Oczekiwanie matematyczne M(X) liczby wystąpień zdarzenia A w n niezależnych próbach jest równe iloczynowi liczby prób i prawdopodobieństwa wystąpienia zdarzenia w każdej próbie.
6.1.3 Rozproszenie dyskretnej zmiennej losowej
Oczekiwanie matematyczne nie może w pełni scharakteryzować procesu losowego. Oprócz oczekiwania matematycznego należy wprowadzić wartość charakteryzującą odchylenie wartości zmiennej losowej od oczekiwania matematycznego.
Odchylenie to jest równe różnicy między zmienną losową a jej oczekiwaniem matematycznym. W tym przypadku matematyczne oczekiwanie odchylenia wynosi zero. Wyjaśnia to fakt, że niektóre możliwe odchylenia są dodatnie, inne ujemne, a w wyniku ich wzajemnego zniesienia uzyskuje się zero.
Dyspersja (rozpraszanie) Dyskretna zmienna losowa nazywana jest oczekiwaniem matematycznym kwadratu odchylenia zmiennej losowej od jej oczekiwań matematycznych.
W praktyce ta metoda obliczania wariancji jest niewygodna, ponieważ prowadzi do uciążliwych obliczeń dla dużej liczby wartości zmiennej losowej.
Dlatego stosuje się inną metodę.
Twierdzenie. Wariancja jest równa różnicy między matematycznym oczekiwaniem kwadratu zmiennej losowej X a kwadratem jej matematycznego oczekiwania.
Dowód. Biorąc pod uwagę fakt, że oczekiwanie matematyczne M (X) i kwadrat oczekiwania matematycznego M 2 (X) są wartościami stałymi, możemy zapisać:
Przykład. Znajdź wariancję dyskretnej zmiennej losowej określonej przez prawo dystrybucji.
| X | ||||
| X2 | ||||
| R | 0.2 | 0.3 | 0.1 | 0.4 |
Rozwiązanie: .
6.1.4 Właściwości dyspersyjne
1. Rozrzut wartości stałej wynosi zero. .
2. Ze znaku dyspersji można usunąć stały współczynnik, podnosząc go do kwadratu. ![]() .
.
3. Wariancja sumy dwóch niezależnych zmiennych losowych jest równa sumie wariancji tych zmiennych. .
4. Wariancja różnicy dwóch niezależnych zmiennych losowych jest równa sumie wariancji tych zmiennych. .
Twierdzenie. Wariancja liczby wystąpień zdarzenia A w n niezależnych próbach, w których każde prawdopodobieństwo p zajścia zdarzenia jest stałe, jest równe iloczynowi liczby prób oraz prawdopodobieństwa wystąpienia i niewystąpienia zdarzenia w każdej próbie.
Przykład: Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w 2 niezależnych próbach, jeśli prawdopodobieństwo wystąpienia zdarzenia w tych próbach jest takie samo i wiadomo, że M(X) = 1,2.
Stosujemy twierdzenie z rozdziału 6.1.2:
M(X) = np
M(X) = 1,2; N= 2. Znajdź P:
1,2 = 2∙P
P = 1,2/2
Q = 1 – P = 1 – 0,6 = 0,4
Znajdźmy dyspersję według wzoru:
D(X) = 2∙0,6∙0,4 = 0,48
6.1.5 Odchylenie standardowe dyskretnej zmiennej losowej
Odchylenie standardowe zmienna losowa X nazywana jest pierwiastkiem kwadratowym wariancji.
![]() (25)
(25)
Twierdzenie. Odchylenie standardowe sumy skończonej liczby wzajemnie niezależnych zmiennych losowych jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń standardowych tych zmiennych.
6.1.6 Tryb i mediana dyskretnej zmiennej losowej
Moda M o DSV nazywa się najbardziej prawdopodobną wartość zmiennej losowej (czyli wartość, która ma największe prawdopodobieństwo)
Mediana M i DSW jest wartością zmiennej losowej, która dzieli szereg rozkładów na pół. Jeżeli liczba wartości zmiennej losowej jest parzysta, wówczas medianę oblicza się jako średnią arytmetyczną dwóch średnich wartości.
Przykład: tryb wyszukiwania i mediana DSW X:
| X | ||||
| P | 0.2 | 0.3 | 0.1 | 0.4 |
Ja = = 5,5
Postęp
1. Zapoznaj się z teoretyczną częścią pracy (wykłady, podręcznik).
2. Wykonaj zadanie według własnego wyboru.
3. Sporządź raport z pracy.
4. Chroń swoją pracę.
2. Cel pracy.
3. Postęp prac.
4. Decyzja o Twojej opcji.
6.4 Warianty zadań do samodzielnej pracy
Opcja numer 1
1. Znajdź matematyczne oczekiwanie, wariancję, odchylenie standardowe, modę i medianę DSV X określoną przez prawo dystrybucji.
| X | ||||
| P | 0.1 | 0.6 | 0.2 | 0.1 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=6, M(Y)=4, Z=5X+3Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w dwóch niezależnych próbach, jeżeli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (X) = 1.
4. Podano listę możliwych wartości dyskretnej zmiennej losowej X: x 1 = 1, x2 = 2, x 3= 5, znane są także matematyczne oczekiwania tej wielkości i jej kwadratu: , . Znajdź prawdopodobieństwa , , , odpowiadające możliwym wartościom , i sporządź prawo dystrybucji DSW.
Opcja numer 2
| X | ||||
| P | 0.3 | 0.1 | 0.2 | 0.4 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=5, M(Y)=8, Z=6X+2Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w trzech niezależnych próbach, jeżeli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (X) = 0,9.
4. Podano listę możliwych wartości dyskretnej zmiennej losowej X: x 1 = 1, x2 = 2, x 3 = 4, x4= 10, znane są także matematyczne oczekiwania tej wielkości i jej kwadratu: , . Znajdź prawdopodobieństwa , , , odpowiadające możliwym wartościom , i sporządź prawo dystrybucji DSV.
Opcja numer 3
1. Znajdź matematyczne oczekiwanie, wariancję i odchylenie standardowe DSV X określone przez prawo dystrybucji.
| X | ||||
| P | 0.5 | 0.1 | 0.2 | 0.3 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=3, M(Y)=4, Z=4X+2Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w czterech niezależnych próbach, jeśli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (x) = 1,2.
Jak już wiadomo, prawo dystrybucji całkowicie charakteryzuje zmienną losową. Jednak prawo dystrybucji jest często nieznane i trzeba ograniczać się do mniejszych informacji. Czasami jeszcze bardziej opłacalne jest użycie liczb opisujących w sumie zmienną losową; takie liczby się nazywają charakterystyka liczbowa zmiennej losowej.
Oczekiwanie matematyczne jest jedną z ważnych cech liczbowych.
Oczekiwanie matematyczne jest w przybliżeniu równe średniej wartości zmiennej losowej.
Oczekiwanie matematyczne dyskretnej zmiennej losowej jest sumą iloczynów wszystkich możliwych wartości i ich prawdopodobieństw.
Jeżeli zmienna losowa charakteryzuje się skończonym szeregiem rozkładów:
| X | x 1 | x 2 | x 3 | … | x rz |
| R | str. 1 | str. 2 | str. 3 | … | r str |
następnie oczekiwanie matematyczne M(X) określa się wzorem:
Matematyczne oczekiwanie ciągłej zmiennej losowej jest określone przez równość:
gdzie jest gęstością prawdopodobieństwa zmiennej losowej X.
Przykład 4.7. Znajdź matematyczne oczekiwanie liczby punktów, które wypadną po rzucie kostką.
Rozwiązanie:
Losowa wartość X przyjmuje wartości 1, 2, 3, 4, 5, 6. Stwórzmy prawo jego dystrybucji:
| X | ||||||
| R |
Zatem oczekiwanie matematyczne wynosi:
Właściwości oczekiwań matematycznych:
1. Matematyczne oczekiwanie na stałą wartość jest równe samej stałej:
M(S)=S.
2. Ze znaku oczekiwania można wyjąć współczynnik stały:
M(CX) = CM(X).
3. Oczekiwanie matematyczne iloczynu dwóch niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
M(XY) = M(X)M(Y).
Przykład 4.8. Niezależne zmienne losowe X I Y wynikają z następujących praw dystrybucji:
| X | Y | ||||||
| R | 0,6 | 0,1 | 0,3 | R | 0,8 | 0,2 |
Znajdź matematyczne oczekiwanie zmiennej losowej XY.
Rozwiązanie.
Znajdźmy matematyczne oczekiwania każdej z tych wielkości:
zmienne losowe X I Y niezależne, więc pożądane oczekiwanie matematyczne:
M(XY) = M(X)M(Y)=
Konsekwencja. Oczekiwanie matematyczne iloczynu kilku wzajemnie niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych.
4. Oczekiwanie matematyczne sumy dwóch zmiennych losowych jest równe sumie oczekiwań matematycznych wyrazów:
M(X + Y) = M(X) + M(Y).
Konsekwencja. Oczekiwanie matematyczne sumy kilku zmiennych losowych jest równe sumie oczekiwań matematycznych tych terminów.
Przykład 4.9. Oddaje się 3 strzały z prawdopodobieństwem trafienia w cel równym str. 1 = 0,4; p2= 0,3 i str. 3= 0,6. Znajdź matematyczne oczekiwanie całkowitej liczby trafień.
Rozwiązanie.
Liczba trafień przy pierwszym strzale jest zmienną losową X 1, które może przyjmować tylko dwie wartości: 1 (trafienie) z prawdopodobieństwem str. 1= 0,4 i 0 (chyba) z prawdopodobieństwem q 1 = 1 – 0,4 = 0,6.
Matematyczne oczekiwanie liczby trafień w pierwszym strzale jest równe prawdopodobieństwu trafienia:
Podobnie znajdujemy matematyczne oczekiwania dotyczące liczby trafień w drugim i trzecim strzale:
M(X 2)= 0,3 i M (X 3) \u003d 0,6.
Całkowita liczba trafień jest również zmienną losową składającą się z sumy trafień w każdym z trzech strzałów:
X \u003d X 1 + X 2 + X 3.
Pożądane oczekiwanie matematyczne X z twierdzenia matematycznego znajdujemy oczekiwanie sumy.







