Parametreli ikinci dereceden denklemler ve eşitsizlikler. Ders Kitabı "Parametreli Denklemler ve Eşitsizlikler" Parametreli Doğrusal Denklemler ve Eşitsizlikler

Bu derste eşitsizlikleri parametrelerle çözmeye yönelik algoritmayı inceleyeceğiz ve bu tür problemleri çözerken onu nasıl uygulayacağımızı öğreneceğiz.

Tanım bir.

Bir eşitsizliği parametreyle çözmek, her parametre değeri için belirli bir eşitsizliğin tüm çözüm kümesini bulmak veya hiçbir çözüm olmadığını kanıtlamak anlamına gelir.

Doğrusal eşitsizlikleri ele alalım.

Tanım iki.

a x artı biçimindeki eşitsizlikler sıfırdan büyük, sıfırdan büyük veya sıfıra eşit, sıfırdan küçük, sıfırdan küçük veya sıfıra eşit olabilir; burada A ve gerçek sayılardır, X- değişken, birinci dereceden eşitsizliklere denir (doğrusal eşitsizlikler).

Doğrusal bir eşitsizliği bir parametreyle çözmek için bir algoritma; örneğin, x artı eşitsizliği sıfırdan büyüktür, burada A ve gerçek sayılardır, X- değişken. Aşağıdaki durumları göz önünde bulundurun:

İlk durum:A sıfırdan büyükse, x eksiden büyükse a'ya bölünür.

Sonuç olarak, eşitsizliğin çözüm kümesi eksiden artı sonsuza bölünen açık bir sayısal ışındır.

İkinci durum:A sıfırdan küçükse x eksiden küçüktür a'ya bölünür

ve dolayısıyla eşitsizliğin çözüm kümesi eksi sonsuzdan eksi a'ya bölünen açık bir sayısal ışındır.

Üçüncü durum: a sıfıra eşitse eşitsizlik şu şekli alacaktır: sıfır çarpı x artı sıfırdan büyük ve for tatlım sıfırdan büyükse herhangi bir gerçek sayı eşitsizliğin çözümüdür ve tatlım Sıfırdan küçük veya sıfıra eşitse eşitsizliğin çözümü yoktur.

Geriye kalan eşitsizlikler de benzer şekilde çözülür.

Örneklere bakalım.

1. Egzersiz

a x eşittir veya birden küçüktür eşitsizliğini çözün.

Çözüm

İşarete bağlı olarak AÜç durumu ele alalım.

İlk durum: eğer A sıfırdan büyükse x, birden küçük veya ona eşittir, bölü a;

İkinci durum: eğer A sıfırdan küçükse x, birden büyük veya ona eşittir, bölü a;

Üçüncü durum: eğer A sıfıra eşitse eşitsizlik şu şekli alacaktır: sıfır ile x çarpımı birden küçüktür veya ona eşittir ve bu nedenle herhangi bir gerçek sayı orijinal eşitsizliğin bir çözümüdür.

Böylece eğer A sıfırdan büyükse, x eksi sonsuzdan bire bölünen ışına aittir.

Eğer A A sıfıra eşit,

O X

Cevap: eğer A sıfırdan büyükse x, eksi sonsuzdan bire bölünen ışına aittir;

Eğer A sıfırdan küçükse, x birden artı sonsuza kadar olan ışına aittir ve eğer A sıfıra eşit,

O X x reel sayılar kümesine aittir.

Görev 2

Eşitsizlik modülünü x eksi iki büyük eksi a ile bir arasındaki farkın karesini çözün.

Çözüm

Herhangi bir reel durum için x eksi iki modülünün sıfırdan büyük veya sıfıra eşit olduğuna dikkat edin. X ve eksi a ile bir arasındaki farkın karesi parametrenin herhangi bir değeri için sıfırdan küçük veya sıfıra eşittir A. Bu nedenle eğer A bire eşitse herhangi biri X- ikiden farklı bir gerçek sayı eşitsizliğin çözümüdür ve eğer A bire eşit değilse, herhangi bir gerçek sayı eşitsizliğin çözümüdür.

Cevap: eğer A bire eşitse x, eksi sonsuzdan ikiye ve ikiden artı sonsuza kadar iki açık sayı ışınının birleşimine aittir,

ve eğer A eksi sonsuzdan bire ve birden artı sonsuza kadar iki açık sayı ışınının birleşimine aitse, o zaman X reel sayılar kümesine aittir.

Görev 3

Eşitsizliği üç çarpı dört a ve x eksi iki a x artı üç farkıyla çözün.

Çözüm

Bu eşitsizliğin temel dönüşümlerinden sonra eşitsizliği elde ederiz: x çarpı iki a ve üçün toplamı üçten büyüktür çarpı dört a ve bir farkıyla.

Birinci durum: eğer iki a artı üç sıfırdan büyükse, bu A eksi üç saniyeden büyükse x, payı dört a ile bir farkının üç katı olan ve paydası iki a artı üç olan bir kesirden büyüktür.

İkinci durum: Eğer iki a artı üç sıfırdan küçükse, bu A eksi üç saniyeden küçükse x, payı dört a ile bir farkının üç katı olan ve paydası iki a artı üç olan bir kesirden küçüktür.

Üçüncü durum: Eğer iki a artı üç sıfıra eşitse, bu A eksi üç saniyeye eşittir,

herhangi bir gerçek sayı orijinal eşitsizliğin bir çözümüdür.

Sonuç olarak, eğer a eksi üç saniyeden artı sonsuza kadar açık sayı doğrusunda yer alıyorsa, o zaman x

payı dört a ve bir farkının üç katı olan ve paydası iki a artı üçten artı sonsuza kadar olan bir kesirden açık bir sayı doğrusuna aittir.

Eğer a, eksi sonsuzdan eksi üç saniyeye kadar açık sayı doğrusuna aitse, o zaman x, payı dört a ve birin farkının üç katı olan ve paydası iki a artı olan eksi sonsuzdan açık sayı doğrusuna aittir. üç;

Eğer A eksi üç saniyeye eşittir, o zaman X reel sayılar kümesine aittir.

Cevap: Eğer a eksi üç saniyeden artı sonsuza kadar açık sayı doğrusunda yer alıyorsa, o zaman x

payı dört a ve bir farkının üç katı olan ve paydası iki a artı üç ila artı sonsuz olan bir kesirden açık bir sayı ışınına aittir;

a, eksi sonsuzdan eksi üç saniyeye kadar olan açık sayı doğrusuna aitse, o zaman x, payı dört a ile birin farkının üç katı olan ve paydası iki a artı olan eksi sonsuzdan bir kesre kadar olan açık sayı doğrusuna aittir. üç;

Eğer A eksi üç saniyeye eşittir, o zaman X reel sayılar kümesine aittir.

Görev 4

Geçerli tüm parametre değerleri için A karekök x eksi a artı karekök iki a eksi x artı karekök a eksi bir artı karekök üç eksi a bölü sıfır eşitsizliğini çözün.

Çözüm

Parametrenin tanım tanım kümesini bulalım A. Bu, a'nın birden üçe kadar olan segmente ait olduğunu bulduğumuz bir eşitsizlik sistemi tarafından belirlenir.

Bu eşitsizlik, x'in a'dan ikiye a'ya kadar olan segmente ait olduğunu bulduğumuz bir eşitsizlikler sistemine eşdeğerdir.

Eğer a, birden üçe kadar olan parçaya aitse, o zaman orijinal eşitsizliğin çözümü, a'dan ikiye kadar olan parçadır.

Cevap: Eğer a, birden üçe kadar olan parçaya aitse, toix, a'dan ikiye kadar olan parçaya aittir.

Görev 5

Hepsini bul A, hangi eşitsizlik için

x'in karekökü eksi x eksi iki artı payı iki eksi x ve paydası x olan bir kesrin karekökü artı dört a x'ten büyük veya ona eşit artı iki eksi payı x artı olan bir kesrin karekökü bir ve payda beş eksi x'in çözümü yok.

Çözüm

Birinci. Bu eşitsizliğin tanım tanım kümesini hesaplayalım. Çözümü iki sayı olan bir eşitsizlik sistemi tarafından belirlenir: x eksi bire ve x ikiye eşittir.

Saniye. Bu eşitsizliğin çözümlerinin olduğu a'nın tüm değerlerini bulalım. Bunun için her şeyi bulacağız A x'in eksi bire ve x'in ikiye eşit olduğu denklem - bu, bu eşitsizliğin çözümüdür. İki sistemden oluşan bir kümeyi ele alalım ve çözelim. Çözüm, eksi sonsuzdan eksi yarıma ve birden artı sonsuza kadar iki sayı ışınını birleştirmektir.

Bu, a'nın eksiden iki sayı ışınının birleşimine ait olması durumunda bu eşitsizliğin bir çözümü olduğu anlamına gelir.

sonsuzdan eksi yarıma ve birden artı sonsuza.

Üçüncü. Sonuç olarak, eğer a eksi yarımdan bire kadar olan aralığa aitse bu eşitsizliğin çözümü yoktur.

Yanıt: Eğer a eksi yarımdan bire kadar olan aralığa aitse eşitsizliğin çözümü yoktur.

Eşitsizlikleri bir parametreyle çözme.

ax > b, ax biçimindeki eşitsizlikler< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются doğrusal eşitsizlikler.

Doğrusal eşitsizlikleri bir parametreyle çözme ilkeleri, doğrusal denklemleri bir parametreyle çözme ilkelerine çok benzer.

Örnek 1.

5x – a > ax + 3 eşitsizliğini çözün.

Çözüm.

İlk önce orijinal eşitsizliği dönüştürelim:

5x – ax > a + 3, eşitsizliğin sol tarafındaki parantezlerden x'i çıkaralım:

(5 – a)x > a + 3. Şimdi a parametresi için olası durumları düşünün:

a > 5 ise x< (а + 3) / (5 – а).

a = 5 ise çözüm yoktur.

Eğer bir< 5, то x >(a + 3) / (5 – a).

Bu çözüm eşitsizliğin cevabı olacaktır.

Örnek 2.

a ≠ 1 için x(a – 2) / (a ​​– 1) – 2a/3 ≤ 2x – a eşitsizliğini çözün.

Çözüm.

Orijinal eşitsizliği dönüştürelim:

x(a – 2) / (a ​​– 1) – 2x ≤ 2a/3 – a;

Ах/(а – 1) ≤ -а/3. Eşitsizliğin her iki tarafını (-1) ile çarparsak şunu elde ederiz:

ax/(a – 1) ≥ a/3. a parametresi için olası durumları inceleyelim:

1 vaka. a/(a – 1) > 0 veya a € (-∞; 0)ᴗ(1; +∞) olsun. O halde x ≥ (a – 1)/3.

Durum 2. a/(a – 1) = 0 olsun, yani. a = 0. O halde x herhangi bir gerçek sayıdır.

Durum 3. a/(a – 1) olsun< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Cevap: x € [(a – 1)/3; +∞) bir € için (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] (0; 1) € karşılığında;
a = 0 için x € R.

Örnek 3.

|1 + x| eşitsizliğini çözün ≤ x'e göre balta.

Çözüm.

Eşitsizlik ekseninin sağ tarafının negatif olmaması gerektiği koşulundan çıkar; ax ≥ 0. |1 + x| eşitsizliğinden modülü açığa çıkarma kuralına göre ≤ balta çift eşitsizliğimiz var

Balta ≤ 1 + x ≤ balta. Sonucu bir sistem biçiminde yeniden yazalım:

(ax ≥ 1 + x;
(-ax ≤ 1 + x.

Bunu şuna dönüştürelim:

((a – 1)x ≥ 1;
((a + 1)x ≥ -1.

Ortaya çıkan sistemi aralıklarla ve noktalarda inceliyoruz (Şekil 1):

≤ -1 x € (-∞; 1/(a – 1)] için.

1'de< а < 0 x € [-1/(а – 1); 1/(а – 1)].

a = 0 x = -1 olduğunda.

0'da< а ≤ 1 решений нет.

Eşitsizlikleri çözmek için grafiksel yöntem

Grafiklerin çizilmesi, bir parametre içeren denklemlerin çözümünü büyük ölçüde basitleştirir. Eşitsizlikleri bir parametreyle çözerken grafik yöntemini kullanmak daha net ve daha uygundur.

f(x) ≥ g(x) formundaki eşitsizliklerin grafiksel olarak çözülmesi, f(x) fonksiyonunun grafiğinin g(x) fonksiyonunun grafiğinin üzerinde yer aldığı x değişkeninin değerlerini bulmak anlamına gelir. Bunu yapmak için her zaman grafiklerin kesişme noktalarını (varsa) bulmak gerekir.

Örnek 1.

|x + 5| eşitsizliğini çözün< bx.

Çözüm.

y = |x + 5| fonksiyonlarının grafiklerini oluşturuyoruz ve y = bx (İncir. 2). Eşitsizliğin çözümü, y = |x + 5| fonksiyonunun grafiği olan x değişkeninin değerleri olacaktır. y = bx fonksiyonunun grafiğinin altında olacaktır.

Resim şunu gösterir:

1) b > 1 için doğrular kesişir. Bu fonksiyonların grafiklerinin kesişme noktasının apsisi x + 5 = bx denkleminin çözümüdür, dolayısıyla x = 5/(b – 1). Y = bx grafiği yukarıda x noktasında (5/(b – 1); +∞) aralığında yer alır, bu da bu kümenin eşitsizliğin çözümü olduğu anlamına gelir.

2) Benzer şekilde bunu -1'de buluyoruz< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) b ≤ -1 x € (-∞; 5/(b – 1)) için.

4) 0 ≤ b ≤ 1 için grafikler kesişmez, bu da eşitsizliğin çözümü olmadığı anlamına gelir.

Cevap: b ≤ -1 için x € (-∞; 5/(b – 1));
x € (-5/(b + 1); 5/(b – 1)) -1'de< b < 0;
0 ≤ b ≤ 1 için çözüm yoktur; b > 1 için x € (5/(b – 1); +∞).

Örnek 2.

a(a + 1)x > (a + 1)(a + 4) eşitsizliğini çözün.

Çözüm.

1) a parametresi için “kontrol” değerlerini bulalım: a 1 = 0 ve 2 = -1.

2) Bu eşitsizliği reel sayıların her bir alt kümesi üzerinde çözelim: (-∞; -1); (-1); (-10); (0); (0; +∞).

a) a< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a = -1 ise bu eşitsizlik 0 x > 0 formunu alacaktır – çözüm yoktur;

c) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0 ise bu eşitsizlik 0 x > 4 şeklinde olur – çözüm yoktur;

e) a > 0, bu eşitsizlikten x > (a + 4)/a sonucu çıkar.

Örnek 3.

|2 – |x|| eşitsizliğini çözün< a – x.

Çözüm.

y = |2 – |x|| fonksiyonunun grafiğini oluşturuyoruz (Şek. 3) ve y = -x + a düz çizgisinin konumuna ilişkin tüm olası durumları göz önünde bulundurun.

Yanıt: ≤ -2 için eşitsizliğin çözümü yoktur;
x € (-∞; (a – 2)/2) için a € (-2; 2];
a > 2 için x € (-∞; (a + 2)/2).

Çeşitli problemleri, denklemleri ve eşitsizlikleri parametrelerle çözerken, matematiğin diğer dallarında başarıyla uygulanabilecek önemli sayıda sezgisel teknik keşfedilir.

Parametrelerle ilgili problemler mantıksal düşünmenin ve matematik kültürünün oluşmasında önemli rol oynar. Bu nedenle parametrelerle problem çözme yöntemlerine hakim olarak diğer problemlerle başarılı bir şekilde başa çıkacaksınız.

Hala sorularınız mı var? Eşitsizlikleri nasıl çözeceğinizi bilmiyor musunuz?
Bir öğretmenden yardım almak için kaydolun.
İlk ders ücretsiz!

web sitesi, materyalin tamamını veya bir kısmını kopyalarken kaynağa bir bağlantı gereklidir.

Seri “Parametrelerle problemleri çözmeyi öğrenme”

IV. Parametreli ikinci dereceden denklemler ve eşitsizlikler

IV.1. Temel konseptler

Tanım. (1) formunda bir fonksiyon; burada , , parametrenin verilen fonksiyonlarıdır A Tanım alanlarının kesişiminde dikkate alınan, parametreli ikinci dereceden bir fonksiyon olarak adlandırılacaktır. A.

Örnekler.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Tanım. Parametreli ikinci dereceden fonksiyonun (1) tanımının alt alanı A değer çiftlerinin tamamını anlayacağız X Ve A tip ( X; A), her biri için ifade anlamını kaybetmez.

1-10 arası fonksiyonların tanım alanlarını oluşturalım.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Parametre sayısal değerlerden birini alırsa , o zaman fonksiyon (1), sayısal katsayılı fonksiyonlardan birinin şeklini alacaktır:

; ; ;
; ; ; ,

Nerede k, B, C- gerçek sayılar.

Parametrenin bazı değerleri için, parametreli ikinci dereceden bir fonksiyonun, parametresiz ikinci dereceden bir fonksiyon veya doğrusal bir fonksiyon şeklini almasına dikkat edelim.

Parametreli ikinci dereceden bir fonksiyon çoğunlukla sayısal katsayılı ikinci dereceden veya doğrusal fonksiyonlar ailesini "oluşturduğundan", parametreli ikinci dereceden bir fonksiyonun grafikleri, bu ailenin birçok grafiğini kastedeceğiz.

Tanım. A(1) formundaki bir denklem denir; burada , , parametrenin bu fonksiyonlarıdır A tanım alanlarının kesiştiği noktada ele alınır.

Özellikle katsayılardan bazıları veya kesme terimi sayı olabilir.

Örnekler.

, (1)
, (2)
, (3)
, (4)
. (5)

Bir parametreli ikinci dereceden bir fonksiyonun tanımını kullanarak, bir parametreli ikinci dereceden bir denklemin aşağıdaki tanımını verebiliriz.

Tanım. Parametreli ikinci dereceden denklem A parametreli ikinci dereceden bir fonksiyon olan formun denklemi denir A.

Eğer ise, o zaman denklem (1) geleneksel anlamda ikinci derecedendir, yani. ikinci derece.
Eğer öyleyse, denklem (1) doğrusal hale gelir.

Geçerli tüm parametre değerleri için A, bunun için ve bilinen formülleri kullanarak denklemin (1) kökleri için parametre cinsinden ifadeler elde ederiz.

Bu değerler A, özel durumlar olarak ayrıca değerlendirilmelidir.
Yani, örneğin denklem (5) formunu alacaktır, bu nedenle.

IV.2. Parametreli ikinci dereceden denklemler

№1. Denklemi çözün.

– denklem-sonuç. Şunu elde ederiz: , .

Koordinat sisteminde ( ah) çözümü tamamlıyoruz. (Şekil 1)

Cevap: 1. Eğer öyleyse, o zaman.

2. Eğer öyleyse .

3. Eğer , o zaman , .

№2. Parametre değerini bulun A Denklemin tek bir kökü vardır. Bu tür birkaç değer varsa, bunların toplamını cevabınıza yazın.

Bu denklem eşdeğer bir sisteme indirgenir:

Bunu forma getirelim: ve koordinat sisteminde grafiksel olarak çözelim ( xOa). (İncir. 2).

Denklemin , ve 'de tek bir kökü vardır.

№3. Tüm değerleri bul Xöyle ki parametrenin herhangi bir değeri için A, (0; 2] aralığına ait olmayan, ifade ifadeye eşit değildir. (USE-2007).

Sorunu yeniden formüle edelim: “Tüm değerleri bulun Xöyle ki parametrenin herhangi bir değeri için denklem kökleri yoktur."
Hadi ifade edelim A başından sonuna kadar X:

1) Let . Daha sonra . Bu nedenle denklemin kökleri vardır. Bu da koşulun sağlanmadığı anlamına gelir.
2) İzin verin. Daha sonra . Koordinat sistemini kullanalım ( xOa). (Şek. 3).

Koşul sağlandı.

№4. Parametreye bağlı olarak kaç kök A bir denklemi var mı?

Modülü genişletelim:

Koordinat sisteminde ( xOy) fonksiyonun bir grafiğini oluşturalım

ve denklem tarafından verilen paralel çizgilerden oluşan bir kalemin birkaç çizgisi. (Şekil 4).

Cevap: 1. Eğer ise kök yoktur.

2. Eğer ise, o zaman bir kök.

3. Eğer ise iki kök vardır.

IV.3. Parametreli ikinci dereceden eşitsizlikler

№5. Eşitsizliği çöz .

1 yol.

Bunu dikkate alalım. O zaman bu eşitsizliğin çözümü herhangi biri için B.(Şekil 5).

Eğer öyleyse, çözüm kümesi koordinat sisteminde gösterilecek olan eşitsizliğe geçiyoruz ( kutu). (Şekil 6).

İncir'i birleştirelim. 5 ve 6.

Ve şimdi Şekil 2'ye göre. 7, dikey düz çizgilerle keserek cevaba ulaşmak kolaydır.

Cevap: 1. Eğer öyleyse, o zaman .
2. Eğer öyleyse .
3. Eğer öyleyse

Yöntem 2.

Eşitsizliği koordinat sisteminde grafiksel olarak çözelim ( xOb):

. (Şekil 8).

İki durumu ele alalım.

1). O zaman eşitsizlik şu şekli alacaktır:
2) , sonra .

Fonksiyonun grafiği ve düzlemin koordinatları eşitsizliği sağlayan noktaları içeren kısmı Şekil 8'de gösterilmektedir.

1. Eğer öyleyse .
2. Eğer öyleyse . 3. Eğer öyleyse .

3 yollu.

Şimdi koordinat sisteminde grafiksel bir çözüm sunalım ( xOy). Bunu yapmak için modülü genişletelim:

İşlevi düşünün .

İkinci dereceden bir üç terimlinin kökleri .

Hadi karşılaştıralım ve.

1) , nereden .

Bütünlüğü elde ederiz. (Şekil 9)

2) , nereden . (Şekil 10).

Sonra yani. .

3) , nereden . (Şekil 11).

Sonra yani. .

Cevap: 1. Eğer öyleyse, o zaman .

2. Eğer öyleyse .
3. Eğer öyleyse .

№6. Tüm parametre değerlerini bulun A, bunun için fonksiyonun en küçük değeri 2'den fazla.

Parametrenin tüm değerlerini bulmanız yeterlidir A, her biri için eşitsizlik herhangi biri için doğrudur . Eşitsizliği formda yeniden yazalım. ., ;

Devlet bütçeli eğitim kurumu

Samara bölgesi ortaöğretim genel eğitimi

2 Nolu Okul adını almıştır. V. Maskina demiryolu Sanat. Klyavlino

Klyavlinsky belediye bölgesi

Samara bölgesi

« Denklemler

Ve

eşitsizlikler

parametrelerle"

öğretici

Klyavlino

öğretici

"Parametreli denklemler ve eşitsizlikler" 10-11. sınıflardaki öğrenciler için

Bu kılavuz, harici bir sınavı geçen seçmeli “Parametreli Denklemler ve Eşitsizlikler” dersinin programının bir ekidir (19 Aralık 2008 tarihli Samara Bölgesi Eğitim ve Bilim Bakanlığı'nın bilimsel ve metodolojik uzman konseyi için önerilen Samara bölgesindeki eğitim kurumlarında kullanım)

Yazarlar

Romadanova Irina Vladimirovna

Klyavlinskaya Ortaöğretim Kurumu'nda matematik öğretmeni

2 Nolu Okul adını almıştır. V. Maskina, Klyavlinsky bölgesi, Samara bölgesi

Serbaeva Irina Alekseevna

Giriş……………………………………………………………3-4

Parametreli doğrusal denklemler ve eşitsizlikler……………..4-7

Parametreli ikinci dereceden denklemler ve eşitsizlikler……………7-9

Parametreli kesirli-rasyonel denklemler……………..10-11

Parametreli irrasyonel denklemler ve eşitsizlikler……11-13

Trigonometrik denklemler ve parametrelerle eşitsizlikler.14-15

Parametreli üstel denklemler ve eşitsizlikler………16-17

Logaritmik denklemler ve parametreli eşitsizlikler......16-18

Birleşik Devlet Sınavının hedefleri………………………………………………………...18-20

Bağımsız çalışma için görevler………………………………21-28

Giriiş.

Parametreli denklemler ve eşitsizlikler.

Bir denklem veya eşitsizlikte bazı katsayılara belirli sayısal değerler verilmemiş, ancak harflerle belirtilmişse, bunlara denir. parametreler, ve denklemin veya eşitsizliğin kendisi parametrik.

Parametreli bir denklemi veya eşitsizliği çözmek için yapmanız gerekenler:

Seçme özel anlam- bu, denklemin veya eşitsizliğin çözümünün değiştiği veya geçtiği parametrenin değeridir.

Tanımlamak geçerli değerler– bunlar denklemin veya eşitsizliğin anlamlı olduğu parametrenin değerleridir.

Bir denklemi veya eşitsizliği parametrelerle çözmek şu anlama gelir:

1) hangi parametre değerlerinde çözümlerin mevcut olduğunu belirleyin;

2) kabul edilebilir her parametre değerleri sistemi için karşılık gelen çözüm kümesini bulun.

Bir parametreli bir denklemi aşağıdaki yöntemleri kullanarak çözebilirsiniz: analitik veya grafiksel.

Analitik metod Hiçbiri gözden kaçırılmayacak birkaç durumu göz önünde bulundurarak bir denklemi inceleme görevini içerir.

Her türden parametrelerle denklemleri ve eşitsizlikleri analitik bir yöntem kullanarak çözmek, durumun ayrıntılı bir analizini ve ihtiyacın ortaya çıktığı tutarlı araştırmayı içerir. "dikkatli kullanım" parametre ile.

Grafik yöntemi sırasıyla parametredeki bir değişikliğin denklemin çözümünü nasıl etkilediğinin belirlenebileceği bir denklem grafiğinin oluşturulmasını içerir. Grafik bazen sorunu çözmek için gerekli ve yeterli koşulları analitik olarak formüle etmenize olanak tanır. Grafik çözüm yöntemi özellikle bir parametreye bağlı olarak bir denklemin kaç kökü olduğunu belirlemeniz gerektiğinde etkilidir ve bunu net bir şekilde görebilme avantajına sahiptir.

§ 1. Doğrusal denklemler ve eşitsizlikler.

Doğrusal Denklem A X = B , Genel formda yazılan parametrelerle bir denklem olarak düşünülebilir; X - Bilinmeyen , A , B - seçenekler. Bu denklem için parametrenin özel veya kontrol değeri, bilinmeyenin katsayısının sıfır olduğu değerdir.

Bir parametreyle doğrusal bir denklem çözülürken, parametrenin özel değerine eşit ve ondan farklı olduğu durumlar dikkate alınır.

Özel parametre değeri A değer A = 0.

B = 0 özel bir parametre değeridir B .

Şu tarihte: B ¹ 0 Denklemin çözümü yoktur.

Şu tarihte: B = 0 denklem şu şekli alacaktır: 0x = 0. Bu denklemin çözümü herhangi bir gerçek sayıdır.

Form eşitsizlikleri ah > B Ve balta < B (bir ≠ 0) doğrusal eşitsizlikler denir. Eşitsizliğin çözüm kümesi ah >B- aralık

(; +), Eğer A > 0 , Ve (-;) , Eğer A< 0 . Benzer şekilde eşitsizlik için

Ah< B çözüm kümesi - aralık(-;), Eğer A > 0, Ve (; +), Eğer A< 0.

Örnek 1. Denklemi çözün balta = 5

Çözüm: Bu doğrusal bir denklemdir.

Eğer bir = 0, o zaman denklem 0 × x = 5çözümü yok.

Eğer A¹ 0, x =- denklemin çözümü.

Cevap: saat A¹ 0,x=

a = 0 için çözüm yoktur.

Örnek 2. Denklemi çözün balta – 6 = 2a – 3x.

Çözüm: Bu doğrusal bir denklemdir, balta – 6 = 2a – 3x (1)

balta + 3x = 2a +6

Denklemi şu şekilde yeniden yazmak: (a+3)x = 2(a+3), iki durumu düşünün:

a= -3 Ve A¹ -3.

Eğer a= -3, o zaman herhangi bir gerçek sayı X denklemin (1) köküdür. Eğer A¹ -3 , denklem (1) tek bir köke sahiptir x = 2.

Cevap:Şu tarihte: a = -3, x R ; en A ¹ -3, x = 2.

Örnek 3. Hangi parametre değerlerinde A Denklemin kökleri arasında

2ah – 4kh – a 2 + 4a – 4 = 0 daha fazla kök var 1 ?

Çözüm: Denklemi çözelim 2ah – 4kh – a 2 + 4a – 4 = 0- Doğrusal Denklem

2(a - 2) x = a 2 – 4a +4

2(a - 2) x = (a – 2) 2

Şu tarihte: bir = 2 denklemi çözme 0x = 0 1'den büyük olan herhangi bir sayı olacaktır.

Şu tarihte: A¹ 2 x =
. Koşullara göre x > 1, yani
>1 ve >4.

Cevap:Şu tarihte: A (2)U(4;∞).

Örnek 4 . Her parametre değeri için A Denklemin kök sayısını bulun ah=8.

Çözüm. balta = 8- Doğrusal Denklem.

sen = A– yatay çizgiler ailesi;

sen = - Grafik bir hiperboldür. Bu fonksiyonların grafiklerini oluşturalım.

Cevap: Eğer bir =0 ise denklemin çözümü yoktur. Eğer bir ≠ 0 O halde denklemin bir çözümü vardır.

Örnek 5 . Grafikleri kullanarak denklemin kaç kökü olduğunu bulun:

|x| = ah – 1.

y =| x | ,

sen = ah – 1– grafik bir noktadan geçen düz bir çizgidir (0;-1).

Bu fonksiyonların grafiklerini oluşturalım.

Cevap: Ne zaman |a|>1- bir kök

en | a|≤1 – Denklemin kökleri yoktur.

Örnek 6 . Eşitsizliği çözün balta + 4 > 2x + a 2

Çözüm : balta + 4 > 2x + a 2
(a – 2) x >A 2 – 4. Üç durumu ele alalım.

Cevap. x > a + 2 en a > 2; X<а + 2, en A< 2; en a=2 hiçbir çözüm yok.

§ 2. İkinci dereceden denklemler ve eşitsizlikler

İkinci dereceden denklem formun bir denklemidir Ah ² + B x + c = 0 , Nerede a≠ 0,

A, B , İle - seçenekler.

İkinci dereceden denklemleri bir parametreyle çözmek için aşağıdaki formülleri kullanarak standart çözüm yöntemlerini kullanabilirsiniz:

1 ) İkinci dereceden bir denklemin diskriminantı: D = B ² - 4 AC , (
²- AC)

2) İkinci dereceden bir denklemin kökleri için formüller:X 1 =
, X 2 =
,

(X 1,2 =
)

İkinci dereceden eşitsizliklere denir

A X 2 + B x + c > 0,A X 2 + B x + c< 0, (1), (2)

A X 2 + B x + c ≥ 0,A X 2 + B x + c ≤ 0,(3), (4)

Eşitsizliğin (3) çözüm kümesi, eşitsizliğin (1) çözüm kümesi ile denklemin birleştirilmesiyle elde edilir. , A X 2 + B x + c = 0. Eşitsizliğin (4) çözüm kümesi de benzer şekilde bulunabilir.

İkinci dereceden bir trinomiyalin diskriminantı ise A X 2 + B x + c sıfırdan küçükse, a > 0 için trinomial tüm x'ler için pozitiftir R.

İkinci dereceden bir üç terimlinin kökleri varsa (x 1 < х 2 ), o zaman a > 0 için kümede pozitiftir(-; x 2 )
(X 2; +) ve aralıkta negatif

(x1;x2 ). Eğer bir< 0, то трехчлен положителен на интервале (х 1; x 2 ) ve tüm x için negatif (-; x 1 )
(X 2; +).

Örnek 1. Denklemi çözün ax² - 2 (a – 1)x – 4 = 0.

Bu ikinci dereceden bir denklemdir

Çözüm: Özel anlam bir = 0.

Şu tarihte: bir = 0 doğrusal bir denklem elde ederiz 2x – 4 = 0. Tek bir kökü var x = 2.

Şu tarihte: a ≠ 0. Diskriminantını bulalım.

D = (a-1)² + 4a = (a+1)²

Eğer a = -1, O D = 0 - bir kök.

yerine koyarak kökü bulalım bir = -1.

-x² + 4x – 4= 0, yani x² -4x + 4 = 0, bunu bulduk x=2.

Eğer a ≠ - 1, O D >0 . Kök formülünü kullanarak şunu elde ederiz:x=
;

X 1 =2, x 2 = -.

Cevap:Şu tarihte: a=0 ve a= -1 Denklemin bir kökü var x = 2; en a ≠ 0 ve

A ≠ - 1 denklemin iki kökü varX 1 =2, x 2 =-.

Örnek 2. Bu denklemin kök sayısını bulun x²-2x-8-a=0 parametre değerlerine bağlı olarak A.

Çözüm. Bu denklemi formda yeniden yazalım. x²-2x-8=a

sen = x²-2x-8- grafik bir paraboldür;

sen =a- yatay çizgilerden oluşan bir aile.

Fonksiyonların grafiklerini oluşturalım.

Cevap: Ne zaman A<-9 denklemin çözümü yoktur; a=-9 olduğunda denklemin bir çözümü vardır; en a>-9 denklemin iki çözümü vardır.

Örnek 3. ne de A eşitsizlik (a – 3) x 2 – 2ax + 3a – 6 >0 x'in tüm değerleri için geçerli mi?

Çözüm.İkinci dereceden bir trinomial, x'in tüm değerleri için pozitiftir, eğer

a-3 > 0 ve D<0, т.е. при а, удовлетворяющих системе неравенств

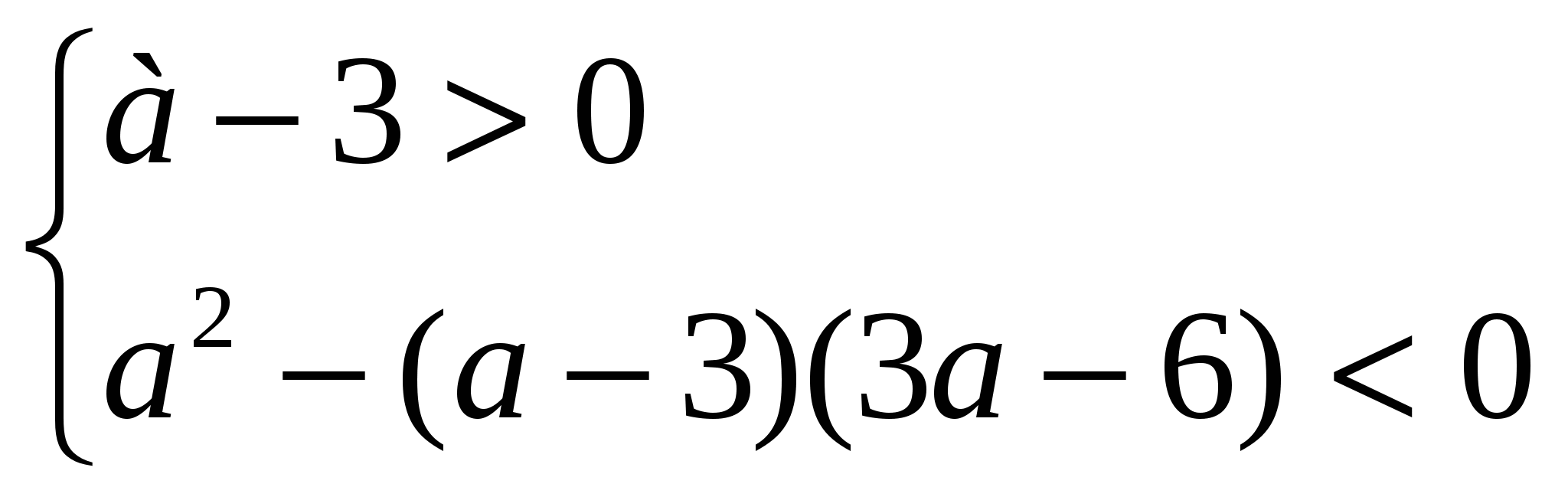
, nereden geliyorA > 6 .

Cevap.A > 6

§ 3. Parametreli kesirli rasyonel denklemler,

doğrusala indirgenebilir

Kesirli denklemleri çözme işlemi olağan şemaya göre gerçekleştirilir: denklemin her iki tarafının sol ve sağ taraflarının ortak paydasıyla çarpılmasıyla kesirin yerini bir tamsayı alır. Bundan sonra, yabancı kökler, yani paydayı sıfıra çeviren sayılar hariç tüm denklem çözülür.

Parametreli denklemlerde bu problem daha karmaşıktır. Burada yabancı kökleri “ortadan kaldırmak” için ortak paydayı sıfıra çeviren parametrenin değerini bulmak, yani parametreye karşılık gelen denklemleri çözmek gerekir.

Örnek 1. Denklemi çözün
= 0

Çözüm: D.Z: x +2 ≠ 0, x ≠ -2

x – a = 0, x = a.

Cevap:Şu tarihte: a ≠ - 2, x=a

Şu tarihte: bir = -2 kök yok.

Örnek 2 . Denklemi çözün
-
=
(1)

Bu kesirli rasyonel bir denklemdir

Çözüm: Anlam bir = 0özeldir. Şu tarihte: bir = 0 denklemin hiçbir anlamı yoktur ve dolayısıyla kökleri yoktur. Eğer a ≠ 0, dönüşümlerden sonra denklem şu şekli alacaktır: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- ikinci dereceden denklem.

Diskriminantını bulalım = (1 – a)² - (a² - 2a – 3)= 4, Denklemin köklerini bulunX 1 = a + 1, x 2 = a - 3.

Denklem (1)'den denklem (2)'ye geçerken, denklem (1)'in tanım alanı genişledi, bu da yabancı köklerin ortaya çıkmasına neden olabilirdi. Bu nedenle doğrulama gereklidir.

Muayene. Bulunan değerlerin dışında bırakalım X içinde olanlar

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Eğer X 1 +1=0, yani (a+1) + 1= 0, O a= -2. Böylece,

en a= -2 , X 1 -

Eğer X 1 +2=0, yani (a+1)+2=0, O bir = - 3. Böylece ne zaman a = - 3, x 1 - Denklemin yabancı kökü. (1).

Eğer X 2 +1=0, yani (a – 3) + 1= 0, O bir = 2. Böylece ne zaman a = 2 x 2 - Denklemin yabancı kökü (1).

Eğer X 2 +2=0, yani ( a – 3) + 2 = 0, O a=1. Böylece ne zaman bir = 1,

X 2 - denklemin yabancı kökü (1).

Buna uygun olarak ne zaman bir = - 3 aldık x = - 3 – 3 = -6;

en a = - 2 x = -2 – 3= - 5;

en a = 1 x =1 + 1= 2;

en a = 2x = 2+1 = 3.

Cevabı yazabilirsiniz.

Cevap: 1) eğer a= -3, O x= -6; 2) eğer a= -2, O x= -5; 3) eğer a= 0, o zaman kök yoktur; 4) eğer a= 1, O x=2; 5) eğer a=2, O x=3; 6) eğer a ≠ -3, a ≠ -2, a ≠ 0, a≠ 1, a ≠ 2, sonra x 1 = a + 1, x 2 = a-3.

§4. İrrasyonel denklemler ve eşitsizlikler

Değişkenin kök işareti altında yer aldığı denklem ve eşitsizliklere denir. mantıksız.

İrrasyonel denklemleri çözmek, denklemin her iki tarafını da üstel alarak veya bir değişkeni değiştirerek irrasyonel bir denklemden rasyonel bir denkleme geçmeyi gerektirir. Denklemin her iki tarafı da eşit kuvvete yükseltildiğinde, yabancı kökler ortaya çıkabilir. Bu nedenle, bu yöntemi kullanırken, bulunan tüm kökleri, parametre değerlerindeki değişiklikleri dikkate alarak orijinal denklemde yerine koyarak kontrol etmelisiniz.

Formun denklemi
=g (x) sisteme eşdeğerdir

f(x) ≥ 0 eşitsizliği f(x) = g 2(x) denkleminden kaynaklanır.

İrrasyonel eşitsizlikleri çözerken aşağıdaki eşdeğer dönüşümleri kullanacağız:

≤ g(x)


≥g(x)

Örnek 1. Denklemi çözün
= x + 1 (3)

Bu irrasyonel bir denklem

Çözüm: Aritmetik kökün tanımı gereği, denklem (3) sisteme eşdeğerdir
.

Şu tarihte: bir = 2 sistemin ilk denklemi şu şekildedir 0 x = 5 yani hiçbir çözümü yoktur.

Şu tarihte: a≠ 2x=
. Bakalım hangi değerlerdeA bulunan değerX eşitsizliği karşılarx ≥ -1:
≥ - 1,
≥ 0,

Neresi a ≤ veya bir > 2.

Cevap:Şu tarihte: a≤, a > 2 x=
, en < а ≤ 2 Denklemin çözümü yoktur.

Örnek 2. Denklemi çözün
= bir (Ek 4)

Çözüm. sen =

sen = bir– yatay çizgiler ailesi.

Fonksiyonların grafiklerini oluşturalım.

Cevap: saat A<0 – hiçbir çözüm yok;

en A≥ 0 - bir çözüm.

Örnek 3 . Eşitsizliği çözelim(a+1)
<1.

Çözüm. O.D.Z. x ≤ 2. Eğer a+1 ≤0, bu durumda eşitsizlik kabul edilebilir tüm değerler için geçerlidir X. Eğer a+1>0, O

(a+1)
<1.

<

Neresi X (2-
2

Cevap. X (- ;2bir (-;-1, X (2-
2

en A (-1;+).

§ 5. Trigonometrik denklemler ve eşitsizlikler.

En basit trigonometrik denklemleri çözmek için formüller şunlardır:

Sinx = a
x= (-1) N arksin a+πn, n Z, ≤1, (1)

Çünkü x = a
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Eğer >1 ise denklem (1) ve (2)'nin çözümü yoktur.

ten rengi x = a
x= arktan a + πn, n Z,a R

CTG x = a
x = arkctg a + πn, n Z,a R

Her standart eşitsizlik için çözüm kümesini belirtiyoruz:

1. günah x > a
arksin a + 2 πn Z,

en A <-1, X R ; en A ≥ 1, hiçbir çözüm yok.

2. . günah x< a
π - arksin a + 2 πnZ,

a≤-1 için çözüm yoktur; > 1 için,X R

3. çünkü X > A
- Arcco'lar A + 2 πn < X < Arcco'lar A + 2 πn , N Z ,

en A<-1, X R ; en A ≥ 1 , hiçbir çözüm yok.

4. çünkü x arccos a+ 2 πnZ,

en a≤-1 , çözüm yok; enA > 1, X R

5. tan x > a, arktan a + πnZ

6.tgx< a, -π/2 + πn Z

Örnek 1. Bulmak A, bu denklemin bir çözümü var:

Çünkü 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Çözüm. Denklemi formda yazalım.

İleişletim sistemi 2 X + (2 A -4) cosx +(A – 5)(a+1) =0, bunu ikinci dereceden denklem olarak çözersek, şunu elde ederiz: cosx = 5-A Ve cosx = -a-1.

Denklem cosx = 5- A çözümleri var -1≤ 5-A ≤1
4≤ A≤ 6 ve Denk. cosx = - a-1 sağlanan -1≤ -1-A ≤ 1
-2 ≤ A ≤0.

Cevap. A -2; 0
4; 6

Örnek 2. ne de Böyle bir eşitsizlik var ki
+ B> 0 tüm x ≠ için geçerlidirπn , N Z .

Çözüm. Hadi koyalım A= 0. Eşitsizlik b >0 için geçerlidir. Şimdi hiçbir b ≤0'ın problemin koşullarını karşılamadığını gösterelim. Aslında x = koymak yeterlidir π /2, Eğer A <0, и х = - π /2 en A ≥0.

Cevap.b>0

§ 6. Üstel denklemler ve eşitsizlikler

1. Denklem H(X) F ( X ) = H(X) G ( X) H(X) > 0 iki sistemin toplamına eşdeğerdir
Ve

2. Özel durumda (h(x)= A ) denklem A f(x) = A g(x) en A> 0, iki sistemin toplamına eşdeğerdir

Ve

3. Denklem A f(x) = B , Nerede A > 0, A ≠1, B>0, denkleme eşdeğer

f (x )= log a b . Olay A=1 ayrı ayrı ele alınır.

En basit üstel eşitsizliklerin çözümü güç özelliğine dayanmaktadır. Formun eşitsizliğiF(A X ) > 0 değişken değişimini kullanarakT= A X eşitsizlik sisteminin çözümüne indirgenir
ve sonra karşılık gelen basit üstel eşitsizliklerin çözümü.

Katı olmayan bir eşitsizliği çözerken, karşılık gelen denklemin köklerini katı eşitsizliğin çözüm kümesine eklemek gerekir. İfadesini içeren tüm örneklerde denklemlerin çözümünde olduğu gibi A f(x), varsayıyoruz A> 0. Durum A= 1 ayrı ayrı ele alınır.

örnek 1 . ne de A denklem 8 x =
sadece pozitif kökleri mi var?

Çözüm. Tabanı birden büyük olan üstel bir fonksiyonun özelliği gereği, x>0 elde ederiz.
8 X >1

>1

>0, neredenA (1,5;4).

Cevap. A (1,5;4).

Örnek 2. Eşitsizliği çözün A 2 ∙2 X > A

Çözüm. Üç durumu ele alalım:

1. A< 0 . Eşitsizliğin sol tarafı pozitif, sağ tarafı negatif olduğundan eşitsizlik herhangi bir x için geçerlidir. R.

2. A=0. Hiçbir çözüm yok.

3. A > 0 . A 2 ∙2 X > bir
2 X >
x > -log 2 A

Cevap. X R en A > 0; için hiçbir çözüm yok A =0; X (- kayıt 2 A; +)a> 0 .

§ 7. Logaritmik denklemler ve eşitsizlikler

Çözümde kullanılan bazı eşdeğerlikleri sunalım. Logaritmik denklemler ve eşitsizlikler.

1. Log f (x) g (x) = log f (x) h (x) denklemi sisteme eşdeğerdir

Özellikle eğer A >0, A≠1 ise

kayıt A g(x)=log A h(x)

2. Denklem kayıt A g(x)=b
g(x)=A B ( A >0, bir ≠ 1, g(x) >0).

3. Eşitsizlik kayıt F ( X ) G (X) ≤ kayıt F ( X ) H(X) iki sistemin birleşimine eşdeğerdir:
Ve

Eğer bir, b sayılardır, a >0, a ≠1, o zaman

kayıt A f(x) ≤ b

kayıt A f(x)>b

Örnek 1. Denklemi çözün

Çözüm. ODZ'yi bulalım: x > 0, x ≠ A 4 , A > 0, A≠ 1. Denklemi dönüştürün

kayıt x – 2 = 4 – kayıt A X
kayıt x + kayıt A X– 6 = 0, dolayısıyla kayıt A X = - 3

x = A-3 ve kayıt A X = 2
x = A 2. Koşul x = A 4
A – 3 = A 4 veya A 2 = A 4 ODZ'de gerçekleştirilmez.

Cevap: x = A-3, x = A 2'de A (0; 1)
(1; ).

Örnek 2 . En büyük değeri bulun A, bunun için denklem

2 kayıt -
+ A = 0'ın çözümleri var.

Çözüm. Bir yedek yapacağız
= Tve ikinci dereceden denklem 2'yi elde ederizT 2 – T + A = 0. Çözüyoruz, buluyoruzD = 1-8 A . Hadi düşünelim D≥0, 1-8 A ≥0
A ≤.

Şu tarihte: A = ikinci dereceden denklemin bir kökü varT= >0.

Cevap. A =

Örnek 3 . Eşitsizliği çözünkayıt(X 2 – 2 X + A ) > - 3

Çözüm. Eşitsizlik sistemini çözelim

Üç terimli karelerin kökleri x 1,2 = 1 ±
onların 3,4 = 1 ±
.

Kritik parametre değerleri: A= 1 ve A= 9.

X 1 ve X 2 birinci ve ikinci eşitsizliklerin çözüm kümeleri olsun, o zaman

X 1
X 2 = X – orijinal eşitsizliğin çözümü.

0'da< A <1 Х 1 = (- ;1 -
)
(1 +
; +), enA> 1 X 1 = (-;+).

0'da< A < 9 Х 2 = (1 -
; 1 +
), enA≥9 X 2 – çözüm yok.

Üç durumu ele alalım:

1. 0< A ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < A < 9 Х = (1 -
;1 +
).

3. A≥ 9 X – çözüm yok.

Birleşik Devlet Sınavı hedefleri

Yüksek seviye C1, C2

Örnek 1. Tüm değerleri bul R, bunun için denklem

R ∙ CTG 2x+2sinx+ P= 3'ün en az bir kökü vardır.

Çözüm. Denklemi dönüştürelim

R ∙ (
- 1) + 2sinx + P= 3, sinx =t, T
,T 0.

- P+2 ton+ P = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = P .

İzin vermek F(sen) = 3 T 2 – 2 T 3 . Fonksiyon değerleri kümesini bulalımF(X) Açık


. en / = 6 T – 6 T 2 , 6 T - 6 T 2 = 0, T 1 =0, T 2 = 1. F(-1) = 5, F(1) = 1.

Şu tarihte: T
, e(F) =
,

Şu tarihte: T
, e(F) =
yani ne zaman T


, e(F) =
.

Denklem 3'eT 2 – 2 T 3 = P (dolayısıyla verilen) gerekli ve yeterli en az bir köke sahiptiP e(F), yani P
.

Cevap.
.

Örnek 2.

Hangi parametre değerlerindeA denklem kayıt
(4 X 2 – 4 A + A 2 +7) = 2'nin tam olarak bir kökü var mı?

Çözüm. Denklemi bunun eşdeğerine dönüştürelim:

4x 2 – 4 A + A 2 +7 = (x 2 + 2) 2.

Belirli bir x sayısı, ortaya çıkan denklemin kökü ise, o zaman – x sayısının da bu denklemin kökü olduğunu unutmayın. Koşullu olarak bu mümkün değildir, dolayısıyla tek kök 0 sayısıdır.

Bulacağız A.

4∙ 0 2 - 4A + A 2 +7 = (0 2 + 2) 2 ,

A 2 - 4A +7 = 4, A 2 - 4A +3 = 0, A 1 = 1, A 2 = 3.

Muayene.

1) A 1 = 1. O zaman denklem şöyle görünür:kayıt
(4 X 2 +4) =2. Haydi çözelim

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 tek köktür.

2) A 2 = 3. Denklem şöyle görünür:kayıt
(4 X 2 +4) =2
x = 0 tek köktür.

Cevap. 1; 3

Yüksek seviye C4, C5

Örnek 3. Tüm değerleri bul R, bunun için denklem

x 2 – ( R+ 3)x + 1= 0'ın tamsayı kökleri vardır ve bu kökler eşitsizliğin çözümleridir: x 3 – 7 R x 2 + 2x 2 – 14 R x - 3x +21 R ≤ 0.

Çözüm. x olsun 1, X 2 – x denkleminin tamsayı kökleri 2 – (R + 3)x + 1= 0. O halde Vieta formülüne göre eşitlikler x 1 + x 2 = R + 3, x 1 ∙ x 2 = 1. İki tam sayının çarpımı x 1 , X 2 yalnızca iki durumda bire eşit olabilir: x 1 =x 2 = 1 veya x 1 =x 2 = - 1. Eğer x 1 =x 2 = 1 iseR + 3 = 1+1 = 2
R = - 1; eğer x 1 =x 2 = - 1 iseR + 3 = - 1 – 1 = - 2
R = - 5. Denklemin köklerinin x olup olmadığını kontrol edelim. 2 – (R + 3)x + 1= 0 açıklanan durumlarda bu eşitsizliğin çözümü. bu vesileyleR = - 1,x 1 =x 2 = 1 elimizde

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – doğru; bu durum için R= - 5, x 1 = x 2 = - 1 elimizde (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – doğru. Yani problemin koşulları yalnızca sağlanır R= - 1 ve R = - 5.

Cevap.R 1 = - 1 ve R 2 = - 5.

Örnek 4. Parametrenin tüm pozitif değerlerini bulun A 1 sayısı fonksiyonun tanım alanına aittir

en = (A
- A
).

Ön izleme:

MOSKOVA BÖLGESİ EĞİTİM BAKANLIĞI

Devlet Eğitim Kurumu NPO 37 Nolu Meslek Yüksekokulu

PROJE:

DÖRTLÜ DENKLEMLER VE PARAMETRELERLE EŞİTSİZLİKLER"

Gerçekleştirildi -

Matsuk Galina Nikolaevna,

Matematik öğretmeni, Devlet Eğitim Kurumu NPO

37 MO numaralı meslek okulu.

G.Noginsk, 2011

1. Giriş

4. İkinci dereceden denklemleri başlangıç ​​koşulları altında çözme metodolojisi.

6. İkinci dereceden eşitsizlikleri genel formdaki parametrelerle çözme metodolojisi.

7. İkinci dereceden eşitsizlikleri başlangıç ​​koşulları altında çözme metodolojisi.

8. Sonuç.

9.Edebiyat.

1. Giriiş.

Bir meslek okulunda matematik öğretmenin temel görevi, öğrencilerin günlük yaşamda ve işte gerekli olan, ilgili disiplinleri incelemek ve sürekli eğitimin yanı sıra mesleki faaliyetlerde yeterli olan matematiksel bilgi ve beceriler sistemine güçlü ve bilinçli bir şekilde hakim olmalarını sağlamaktır. yeterince yüksek bir matematik kültürü gerektirir.

Profilli matematik eğitimi, metal işleme, elektrik tesisatı işleri ve ahşap işleme meslekleriyle ilgili uygulamalı problemlerin çözülmesi yoluyla gerçekleştirilir. Modern toplumdaki yaşam için, belirli zihinsel becerilerde kendini gösteren matematiksel bir iletişim tarzının geliştirilmesi önemlidir. Parametrelerle ilgili sorunların tanısal ve prognostik değeri vardır. Onların yardımıyla, ilköğretim matematiğin ana bölümlerine ilişkin bilginizi, mantıksal düşünme düzeyini ve ilk araştırma becerilerini test edebilirsiniz.

Parametreli görevlerin öğretilmesi, öğrencilerin büyük zihinsel ve istemli çaba göstermelerini, dikkatlerini geliştirmelerini ve etkinlik, yaratıcı inisiyatif ve kolektif bilişsel çalışma gibi niteliklerin geliştirilmesini gerektirir. Parametrelerle ilgili problemler, nihai durum sertifikasyonuna hazırlık için 2. yılda genel tekrar sırasında ve Birleşik Devlet Sınavı şeklinde final sınavlarına girme isteğini ifade eden öğrencilere hazırlık için 3. yılda ek derslerde çalışmaya yöneliktir. .

Matematik eğitiminin modernizasyonunun ana yönü, Birleşik Devlet Sınavının başlatılması yoluyla nihai sertifikasyon mekanizmalarının geliştirilmesidir. Son yıllarda matematik ödevlerinde parametrelerle ilgili problemler ortaya çıkmıştır. Bu tür görevler üniversiteye giriş sınavları için zorunludur. Bu tür problemlerin ortaya çıkması çok önemlidir, çünkü onların yardımıyla başvuranın temel matematik formülleri konusundaki ustalığını, denklemleri ve eşitsizlikleri çözme yöntemlerini, mantıksal bir akıl yürütme zinciri oluşturma yeteneğini ve başvuranın mantıksal düşünme düzeyini test ederler. . Önceki birkaç yıldaki Birleşik Devlet Sınavı sonuçlarının bir analizi, mezunların bu tür görevleri çözmede büyük zorluk yaşadıklarını ve birçoğunun bunlara başlamadığını bile gösteriyor. Çoğu ya bu tür görevlerle hiç baş edemiyor ya da hantal hesaplamalar yapamıyor. Bunun nedeni ise okul ders kitaplarında bu konuyla ilgili bir ödev sisteminin bulunmamasıdır. Bu bağlamda, mesleki yönelim ile ilgili parametrelerle ilgili problemlerin ve uygulamalı nitelikteki problemlerin çözümüne yönelik sınavlara hazırlık için lisansüstü gruplarında özel konuların yürütülmesine ihtiyaç vardı.

Bu konuların incelenmesi, cebirde karmaşıklık düzeyi artan problemlerin nasıl çözüleceğini ve analizin başlangıcını öğrenmek isteyen 3. sınıf öğrencilerine yöneliktir. Bu tür sorunları çözmek onlara önemli zorluklar yaşatıyor. Bunun nedeni, parametreli her denklem veya eşitsizliğin, her biri için bir çözüm elde edilmesi gereken sıradan denklemler ve eşitsizliklerin tamamını temsil etmesidir.

Parametrelerle ilgili problemleri çözme sürecinde, insan düşüncesinin teknik ve yöntemlerinin cephaneliği doğal olarak tümevarım ve tümdengelim, genelleme ve spesifikasyon, analiz, sınıflandırma ve sistemleştirme ve analojiyi içerir. Meslek yüksekokullarındaki müfredat, yeterli matematik eğitimi olan, çalışılan konuya ilgi duyan ve üniversiteye girme hedefi olan öğrencilere ders programında yer alan matematik danışmanlığı sağladığından, Olimpiyatlara, matematik yarışmalarına, çeşitli sınav türlerine, özellikle Birleşik Devlet Sınavına hazırlık için parametrelerle ilgili problemleri çözmek için belirtilen saatleri kullanmak. Bu tür sorunların çözümü, özellikle çeşitli çalışmaların yürütülmesine yardımcı olacak uygulamalı ve pratik amaçlarla ilgilidir.

2. Hedefler, ana görevler, yöntemler, teknolojiler, bilgi gereksinimleri.

Proje hedefleri:

• İkinci dereceden denklemler ve eşitsizliklerin incelenmesine indirgenen parametrelerle problem çözmede yetenek ve becerilerin oluşturulması.
• Konuya ilgi oluşturmak, matematiksel yetenekleri geliştirmek, Birleşik Devlet Sınavına hazırlanmak.
• Denklemleri ve eşitsizlikleri çözmeye yönelik teknik ve yöntemlerin matematiksel anlayışının genişletilmesi.
• Mantıksal düşünme ve araştırma becerilerinin geliştirilmesi.
• Yaratıcı, araştırma ve eğitim faaliyetlerine katılım.
• Bağımsız yaratıcı çalışma için koşullar sağlamak.
• Öğrencilerin zihinsel ve istemli çabalarını teşvik etmek, dikkati, aktiviteyi, yaratıcı inisiyatifi ve kolektif bilişsel çalışma becerilerini geliştirmek.

Projenin ana hedefleri:

• Öğrencilere matematiğe olan ilgilerini gerçekleştirme fırsatı ve matematiğin gelişimi için bireysel fırsatlar sağlamak.
• Gerçek bilgi ve becerilerin edinilmesini teşvik edin.
• Uygulamalı araştırma alanındaki parametrelerle ilgili problemlerin pratik önemini gösterin.
• Standart ve standart dışı denklemleri ve eşitsizlikleri çözme yöntemlerini öğretin.
• Matematikte bilgiyi derinleştirmek, konuya sürdürülebilir ilginin oluşmasını sağlamak.
• Öğrencilerin matematiksel yeteneklerini belirleyin ve geliştirin.
• Üniversitelere giriş için hazırlık sağlayın.
• Yüksek matematik kültürü gerektiren mesleki faaliyetlere hazırlık sağlayın.
• Entelektüel ve iletişim becerilerinin gelişimini teşvik eden araştırma ve proje faaliyetleri düzenlemek.

Derslerde kullanılan yöntemler:

• Ders – öğrencilerle yapılan bir konuşma eşliğinde teorik materyalin aktarılması.
• Seminerler - teorinin tartışılmasına ilişkin materyali pekiştirmek için.
• Atölye çalışmaları – matematik problemlerini çözmek için.
• Tartışmalar – çözümleriniz için argümanlar sağlamak.
• Çeşitli grup ve bireysel aktivite biçimleri.
• Şu şekilde düzenlenen araştırma faaliyetleri: didaktik materyalle çalışma, mesajların hazırlanması, özetlerin ve yaratıcı çalışmaların savunulması.
• Dersler – bilgisayar ve projektör kullanılarak yapılan sunumlar.

Kullanılan teknolojiler:

• Ders-seminer eğitim sistemi.
• Bilgi ve iletişim teknolojileri.
• Öğretimde düşünme becerilerini geliştirmeyi amaçlayan bir araştırma yöntemi.
• Bir problem ortaya koyarak, probleme yönelik çeşitli seçenekleri tartışarak araştırmaya yönelik motivasyon sağlayan probleme dayalı öğrenme.
• Öğrencilerin bilişsel ilgi alanlarını geliştirmeye yardımcı olan etkinlik yöntemi teknolojisi.

Öğrencilerin bilgi gereksinimleri.

İkinci dereceden denklemleri ve eşitsizlikleri parametrelerle çözmenin çeşitli yollarını incelemenin bir sonucu olarak, öğrenciler aşağıdaki becerileri kazanmalıdır:

• İkinci dereceden denklem ve ikinci dereceden eşitsizlikte parametre kavramını iyice kavramak;
• İkinci dereceden denklemleri parametrelerle çözebilme.
• İkinci dereceden eşitsizlikleri parametrelerle çözebilir.
• İkinci dereceden bir fonksiyonun köklerini bulun.
• İkinci dereceden fonksiyonların grafiklerini oluşturun.
• İkinci dereceden trinomial'i keşfedin.
• Kimlik dönüşümlerinde rasyonel yöntemleri uygular.
• En sık kullanılan buluşsal teknikleri kullanın.
• Edinilen bilgileri kişisel bilgisayarda çalışırken uygulayabilme.

Kontrol biçimleri.

• Dersler – öz değerlendirmeler ve yoldaşların değerlendirmeleri.
• Eğitim projelerinin sunumu.
• Test yapmak.
• Derecelendirme – tablo.
• Önceki yılların Birleşik Devlet Sınavı koleksiyonlarından ev ödevi sorunları.
• Test kağıtları.

3. Genel formdaki parametrelerle ikinci dereceden denklemleri çözme metodolojisi.

Parametrelerle ilgili sorunlardan korkmayın. Öncelikle denklem ve eşitsizlikleri parametrelerle çözerken, herhangi bir denklem ve eşitsizliği çözerken yapılması gerekenleri yapmanız gerekir - verilen denklemleri veya eşitsizlikleri mümkünse daha basit bir forma indirin: rasyonel ifadeyi çarpanlara ayırın, azaltın, parantezlerin dışındaki faktörler vb. d. İki büyük sınıfa ayrılabilecek sorunlar var.

Birinci sınıf, bir parametrenin tüm olası değerleri için bir denklemi veya eşitsizliği çözmenin gerekli olduğu örnekleri içerir.

İkinci sınıf, tüm olası çözümlerin değil, yalnızca bazı ek koşulları sağlayanların bulunmasının gerekli olduğu örnekleri içerir. Bu tür sorunların sınıfı tükenmez.

Öğrenciler için bu tür problemleri çözmenin en anlaşılır yolu önce tüm çözümleri bulmak, daha sonra ek koşulları sağlayanları seçmektir.

Parametrelerle ilgili problemleri çözerken, bazen normal düzlemde (x, y) grafikler oluşturmak uygun olur ve bazen de x'in bağımsız değişken ve "a" olduğu düzlemdeki (x, a) grafikleri dikkate almak daha iyidir. parametredir. Bu öncelikle tanıdık temel grafikler oluşturmanız gereken bir problemde mümkündür: düz çizgiler, paraboller, daireler vb. Ek olarak, grafik çizimleri bazen çözümün "ilerlemesini" net bir şekilde görmeye yardımcı olur.

F (x,a) = 0 denklemlerini ve f (x,a) › 0 eşitsizliklerini çözerken, öncelikle katsayının en yüksek olduğu parametre değerleri için çözümün dikkate alındığını unutmamalıyız. kare trinomial f(x,a)'nın kuvveti x, böylece dereceyi azaltır. İkinci dereceden denklem A(a) x 2 A(a) = 0'da + B(a) x + C(a) = 0, eğer B(a) ≠ 0 ise doğrusala dönüşür ve ikinci dereceden ve doğrusal denklemleri çözme yöntemleri farklıdır.

İkinci dereceden denklemlerle çalışmanın temel formüllerini hatırlayalım.

Ah formunun denklemi 2 + in + c = 0, burada x  R bilinmeyenlerdir, a, b, c yalnızca parametrelere bağlı ifadelerdir ve a ≠ 0 ikinci dereceden denklem olarak adlandırılır ve D = b 2 – 4ac’a ikinci dereceden bir trinomiyalin diskriminantı denir.

Eğer D

D > 0 ise denklemin iki farklı kökü vardır

x 1 = , x 2 = ve sonra ax 2 + in + c = a (x – x 1) (x – x 2).

Bu kökler Vieta formülleriyle denklemin katsayıları aracılığıyla ilişkilendirilir.

Eğer D = 0 ise denklemin çakışan iki kökü vardır x 1 = x 2 = ve sonra ax 2 + in + c = a (x – x 1) 2 . Bu durumda denklemin tek çözümü olduğu söylenir.

Ne zaman, yani = 2k, ikinci dereceden denklemin kökleri x formülüyle belirlenir 1,2 = ,

İndirgenmiş ikinci dereceden denklem x'i çözmek için 2 + piksel + q = 0

Kullanılan formül x'tir 1,2 = - Vieta'nın formüllerinin yanı sıra

Örnekler. Denklemleri çözün:

Örnek 1. + =

Çözüm:

a ≠ - 1, x ≠ 2 için x elde ederiz 2 + 2ax – 3b + 4 = 0 ve kökler

x 1 = - bir - , x 2 = -a + , mevcut

A 2 + 2a – 4  0, yani. en

Şimdi herhangi bir x'in olup olmadığını kontrol edelim. 1 veya x 2 2'ye eşittir. İkinci dereceden denklemde x = 2'yi yerine koyarsak = - 8 elde ederiz.

Bu durumda ikinci kök eşittir(Vieta teoremine göre) ve a = - 8 için 14'e eşittir.

Yanıt: a = - 8 için tek çözüm x = 14'tür;

Eğer a  (- ∞; - 8)  (- 8; - 4)  (1; + ∞) – iki kök x 1 ve x2;

Eğer bir = - tek çözüm x =sırasıyla;

a  (- 4; 1) ise x   .

Bazen kesirli terimleri olan denklemler ikinci dereceden terimlere indirgenir. Aşağıdaki denklemi göz önünde bulundurun.

Örnek 2. - =

Çözüm: a = 0 olduğunda mantıklı değildir, x değeri şu koşulları karşılamalıdır: x -1, x  -2. Denklemin tüm terimlerinin a (x + 1) (x +2) ile çarpılması 0,

x 2 – 2(a – 1)x + a 2 elde ederiz – 2a – 3 = 0, buna eşdeğerdir. Kökleri:

x 1 = a + 1, x 2 = - 3. Bu köklerden yabancı kökleri seçelim, yani. -1 ve -2'ye eşit olanlar:

X 1 = a + 1 = - 1, a = - 2, ancak a = - 2 x ile 2 = - 5;

X 1 = a + 1 = - 2, a = - 3, ancak a = - 3 x ile 2 = - 6;

X 2 = a - 3 = - 1, a = 2, ancak a = 2 x ile 1 = 3;

X 2 = a - 3 = - 2, a = 1, ancak a = 1 x ile 1 = 2.

Cevap: a ≠ 0 için a ≠ 2, a ≠ - 3, a ≠ 1 x 1 = a + 1, x 2 = a – 3;

a = - 2 x = - 5 olduğunda; a = - 3 x = - 6 olduğunda.

4. İkinci dereceden denklemleri başlangıç ​​koşulları altında çözme metodolojisi.

Parametrik ikinci dereceden denklemlerin koşulları çeşitlidir. Örneğin, kökleri pozitif, negatif, farklı işaretlere sahip, belirli bir sayıdan büyük veya küçük vb. olan bir parametrenin değerini bulmanız gerekir. Bunları çözmek için ikinci dereceden denklem ax'in köklerinin özelliklerini kullanmalısınız. 2 + inç + c = 0.

D > 0, a > 0 ise denklemin iki gerçek farklı kökü vardır; c > 0 için işaretleri aynı ve b katsayısının işaretiyle zıttır ve c için

D = 0, a > 0 ise denklemin gerçek ve eşit kökleri vardır ve bunun işareti b katsayısının işaretinin tersidir.

Eğer D 0 ise denklemin reel kökleri yoktur.

Benzer şekilde, ikinci dereceden denklemin köklerinin özelliklerini bir

1. İkinci dereceden bir denklemde a ve c katsayılarını değiştirirsek, kökleri verilen denklemin köklerinin tersi olan bir denklem elde ederiz.
2. İkinci dereceden bir denklemde b katsayısının işaretini değiştirirsek, kökleri verilenin köklerinin tersi olan bir denklem elde ederiz.
3. İkinci dereceden bir denklemde a ve c katsayıları farklı işaretlere sahipse, bu denklemin gerçek kökleri vardır.
4. a > 0 ve D = 0 ise ikinci dereceden denklemin sol tarafı tam karedir ve tam tersi, denklemin sol tarafı tam kare ise a > 0 ve D = 0'dır.
5. Denklemin tüm katsayıları rasyonel ise ve diskriminant tam kareyi ifade ediyorsa denklemin kökleri rasyoneldir.
6. Köklerin sıfıra göre konumunu dikkate alırsak Vieta teoremini uygularız.

İkinci dereceden bir üç terimlinin köklerinin, ikinci dereceden bir fonksiyonun sayı doğrusu üzerindeki sıfırlarının koşullarına ve konumuna göre seçimi.

f (x) = ax 2 + in + c, a  0, kökler x 1 ˂ x 2,  ˂  olsun.

	Köklerin sayı doğrusu üzerindeki konumu.	Gerekli ve yeterli koşul.
	x 1, x 2 	ve f ( ) > 0, D  0, x 0 
	x 1, x 2 > 	ve f ( ) > 0, D  0, x 0 > 
	x 1  2	ve f ( )
	 1,x2  .	ve f ( ) > 0, D  0 ve f ( ) > 0  0  .
	 1  2	ve f ( ) > 0 ve f ( )
	x 1  2 	ve f ( )  ) > 0
	x 1   2	ve f ( )  )

Örnek 3. Bir denklemin hangi değerlerinde olduğunu belirleyin

x 2 – 2 (a – 1) x + 2a + 1 = 0

• kökleri yoktur:

gerekli ve yeterli koşul D

D = (a – 1) 2 – 2a – 1 = a 2 – 4a

• kökleri vardır:

D  0, D = (a – 1) 2 – 2a – 1  0, a 

• bir kökü vardır:

• iki kökü vardır:

D > 0, yani. bir 

• pozitif kökleri vardır:

2(a – 1) > 0   a  4

Soru "iki pozitif kökü var" ise sistem değiştirilmelidir D > 0;

• negatif kökleri vardır:

2(a – 1)  

• farklı işaretlerin kökleri vardır, yani. biri olumlu, diğeri olumsuz:

  bir ;

Durum Kullanmaya gerek yok x yeterli 1 x 2

• Köklerden biri 0'a eşit:

gerekli yeterli koşul, denklemin serbest teriminin sıfıra eşit olmasıdır; 2a + 1 = 0, a = -1/2.

İkinci kökün işareti ya orijinal denklemde a = -1/2 yerine koyularak ya da daha basit bir şekilde Vieta'nın x teoremi ile belirlenir. 1 + x 2 = 2 (a – 1) ve a = -1/2'yi değiştirdikten sonra x elde ederiz 2 = - 3, yani a = -1/2 için iki kök: x 1 = 0, x 2 = - 3.

Örnek 4 . Denklem a parametresinin hangi değerlerinde yapılır?

(a – 2) x 2 – 4ax +3 -2a = 0'ın x eşitsizliğini sağlayan tek bir çözümü vardır

Çözüm.

Ayırıcı 2 – (a – 2)(3 – 2a)

4a 2 – 3a + 6 + 2a 2 – 4a = 6a 2 – 7a + 6

49 – 144 = - 95 olduğundan ve ilk katsayı 6 sonra tüm x  R için 6a 2 – 7a + 6.

O halde x 1,2 = .

Problemin koşullarına göre x2, o zaman eşitsizliği elde ederiz

Sahibiz:

tüm a  R için doğrudur.

6a 2 – 7a + 6 6a 2 – 7a - 10 2

A 1,2 = 1/12 (7  17) ve 1 = 2 ve 2 = - 5/6.

Bu nedenle -5/6

Cevap: -

5. Eşit değişken olarak parametre.

Analiz edilen tüm görevlerdeparametre sabit ancak bilinmeyen bir sayı olarak değerlendirildi. Bu arada, resmi bir bakış açısından, bir parametre bir değişkendir ve örnekte mevcut olan diğer parametrelere "eşittir". Örneğin, f(x;a) form parametresinin bu görünümüyle, fonksiyonlar (daha önce olduğu gibi) bir değişkenle değil, iki değişkenle tanımlanır. Böyle bir yorum doğal olarak parametrelerle ilgili problemlerin başka bir türünü (veya daha doğrusu bu türü tanımlayan bir çözüm yöntemini) oluşturur. Bu tipte analitik bir çözüm gösterelim.

Örnek 5. xy düzleminde, y = x ailesi eğrilerinden hiçbirinin geçmediği tüm noktaları belirtin 2 – 4рх + 2р 2 – 3, burada p bir parametredir.

Çözüm: Eğer (x 0;y 0 ) belirli bir ailenin eğrilerinden hiçbirinin geçmediği bir nokta ise bu noktanın koordinatları orijinal denklemi sağlamaz. Sonuç olarak sorun, x ile y arasında, koşulda verilen denklemin hiçbir çözümü olmayacak şekilde bir ilişki bulmaktan ibaretti. İstenilen bağımlılığı x ve y değişkenlerine değil p parametresine odaklanarak elde etmek kolaydır. Bu durumda verimli bir fikir ortaya çıkıyor: Bu denklemi p'ye göre ikinci dereceden olarak düşünün. Sahibiz

2р 2 – 4рх+ x 2 – y – 3 = 0. Diskriminant= 8x2 + 8y + 24 negatif olmalı. Buradan y ˂ - x'i elde ederiz 2 – 3, bu nedenle gerekli küme, koordinat düzleminin y = - x parabolünün “altında” bulunan tüm noktalarıdır. 2 – 3.

Cevap: y 2 – 3

6. İkinci dereceden eşitsizlikleri parametrelerle çözme metodolojisi

Genel olarak.

Formun ikinci dereceden (katı ve katı olmayan) eşitsizlikleri

Kabul edilebilir değerler a, b, c'nin geçerli olduğu parametre değerleridir. İkinci dereceden eşitsizlikleri analitik veya grafiksel olarak çözmek uygundur. İkinci dereceden bir fonksiyonun grafiği bir parabol olduğundan, a > 0 için parabolün dalları yukarıya doğru yönlendirilir.

f(x) = ax parabolünün farklı konumları 2 + inç + s, a  a > 0 için 0 Şekil 1'de gösterilmektedir.

A) b) c)

a) f(x) > 0 ve D R ise;

b) Eğer f(x) > 0 ve D = 0 ise x ;

c) Eğer f(x) > 0 ve D > 0 ise x (-  ; x 1 )  (x 2 ; +  ).

Parabolün konumları benzer şekilde kabul edilir.

Örneğin, üç durumdan biri

a 0 ve f(x) > 0 x  (x 1; x 2) için;

a 0 ve f (x)  (-  ; x 1 )  (x 2 ; +  ) için.

Örnek olarak bir eşitsizliği çözmeyi düşünün.

Örnek 6. Eşitsizliği çöz x 2 + 2x + a > 0.

D üçlü x'in diskriminantı olsun 2 + 2x + a > 0. D = 0 için, a = 1 için eşitsizlik şu formu alır:

(x + 1) 2 > 0

Bu, x = - 1 dışında x'in tüm gerçek değerleri için doğrudur.

D > 0 için, yani. x'te, üç terimli x 2 + 2x + a'nın iki kökü vardır: - 1 – Ve

1 + ve eşitsizliğin çözümü aralıktır

(-  ; - 1 – )  (- 1 + ; +  )

Bu eşitsizliği grafiksel olarak çözmek kolaydır. Bunu yapmak için formda temsil edelim.

X 2 + 2x > - a

ve y = x fonksiyonunun grafiğini oluşturun 2 + 2x

Bu grafiğin y = - a doğrusu ile kesiştiği noktaların apsisleri x denkleminin kökleridir 2 + 2x = - a.

Cevap:

–a > - 1 için, yani. bir, x  (-  ; x 1 )  (x 2 ;+  );

– a = - 1'de, yani a = 1 için x, -1 dışında herhangi bir gerçek sayıdır;

en – bir yani a > 1 için x herhangi bir reel sayıdır.

Örnek 7 . Eşitsizliği çözün cx 2 – 2 (s – 1)x + (s + 2)

c = 0 olduğunda şu formu alır: 2x + 2çözüm x olacak

f(x) = cx gösterimini tanıtalım 2 – 2 (s – 1)x + (s + 2) burada c ≠ 0.

Bu durumda f(x) eşitsizliği

f(x)'in diskriminantı D olsun. 0,25 D = 1 – 4s.

Eğer D > 0 ise, yani. eğer ile> 0,25, o zaman f (x) işareti, x'in herhangi bir gerçek değeri için c işaretiyle çakışır, yani. f(x) Herhangi bir x  R için > 0, yani c > 0,25 eşitsizliği f(x)

Eğer D = 0 ise, yani. c = 0,25, sonra f (x) = (0,25 x + 1,5) 2, yani f(x)  0 herhangi biri için

X  R. Dolayısıyla c = 0,25 için f(x) eşitsizliği

D  durumunu düşünün 0). x'in iki gerçek değeri için f(x) = 0:

x 1 = (c – 1 – ) ve x 2 = (c – 1 + ).

Burada iki durum ortaya çıkabilir:

f(x) eşitsizliğini çözün

f(x) c'nin işaretiyle örtüşmektedir. Bu soruyu yanıtlamak için şunu unutmayın: yani s – 1 – ˂ s – 1 + , ancak s (s – 1 – ) olduğundan (s – 1 + ) ve dolayısıyla eşitsizliğin çözümü şöyle olacaktır:

(-  ; (s – 1 – ))  ( (s – 1 + ); +  ).

Şimdi eşitsizliği çözmek için, f (x) işaretinin c işaretinin karşısında olduğu c değerlerini belirtmek yeterlidir. 0 1'den beri 2, sonra x  (x 1; x 2).

Cevap: c = 0 x R olduğunda;

İle  (-  ; x 2 )  (x 1 ; +  );

0'da  (x 1; x 2);

c  0,25 için çözüm yoktur.

Bir parametrenin eşit bir değişken olarak görülmesi, ikinci dereceden eşitsizliklerin çözümüne yönelik grafiksel yöntemlere yansıtılır. Aslında parametrenin değişkene “hakları eşit” olduğundan, kendi koordinat eksenine “tahsis edilebilmesi” doğaldır. Böylece bir (x; a) koordinat düzlemi ortaya çıkar. Eksenleri belirtmek için geleneksel x ve y harfleri seçiminin terk edilmesi gibi küçük bir ayrıntı, parametrelerle ilgili problemlerin çözümünde en etkili yöntemlerden birini belirler.

Sorunun bir a parametresi ve bir x değişkeni içermesi uygundur. Çözüm sürecinin kendisi şematik olarak buna benziyor. İlk önce bir grafik görüntü oluşturulur, daha sonra ortaya çıkan grafiği parametrik eksene dik düz çizgilerle keserek gerekli bilgileri "kaldırırız".

Eksenleri belirlemek için x ve y harflerinin geleneksel seçiminin reddedilmesi, parametrelerle ilgili problemlerin çözümünde en etkili yöntemlerden birini belirler - "etki alanı yöntemi"

1. Başlangıç ​​koşulları altında ikinci dereceden eşitsizlikleri çözme metodolojisi.

Sonuçları sayı doğrusunda dikkate alınan parametrelerle ikinci dereceden bir eşitsizliğin analitik bir çözümünü ele alalım.

Örnek 8.

Eşitsizliğin her biri için x'in tüm değerlerini bulun

(2x)a 2 +(x 2 -2x+3)a-3x≥0

[-3;0] aralığına ait herhangi bir değer için sağlanır.

Çözüm. Bu eşitsizliğin sol tarafını şu şekilde dönüştürelim:

(2-x)a 2 + (x 2 -2x+3)a-3x=ax 2 - a 2 x - 2ax + 2a 2 + 3a - 3x =

Ax (x - a)-2a(x - a)- 3(x-a) = (x - a)(ax- 2a - 3).

Bu eşitsizlik şu şekilde olacaktır: (x - a) (ax - 2a - 3) ≥ 0.

a = 0 ise - Zx ≥ 0 x ≤ 0 elde ederiz.

a ≠ 0 ise -3 a

Çünkü A 0 ise bu eşitsizliğin çözümü, eşitsizliğe karşılık gelen denklemin kökleri arasında bulunan sayısal eksenin aralığı olacaktır.

Sayıların göreceli konumunu bulalım bir ve , koşulu dikkate alarak - 3 ≤ a

3 ≤a

bir = -1.

Ele alınan tüm durumlarda, parametre değerlerine bağlı olarak bu eşitsizliğin çözümlerini sunalım:

a parametresinin herhangi bir değeri için bu eşitsizliğe yalnızca x = -1'in çözüm olduğunu bulduk. .

Cevap 1

8. Çözüm.

Neden “İkinci dereceden denklemleri ve eşitsizlikleri parametrelerle çözmek için metodolojik önerilerin geliştirilmesi” konulu bir projeyi seçtim? Herhangi bir trigonometrik, üstel, logaritmik denklemleri, eşitsizlikleri, sistemleri çözerken, çoğu zaman bazen doğrusal ve çoğunlukla ikinci dereceden denklemleri ve eşitsizlikleri dikkate alırız. Parametrelerle karmaşık problemleri çözerken, çoğu görev, eşdeğer dönüşümler kullanılarak aşağıdaki türdeki çözümlerin seçimine indirgenir: a (x – a) (x – c) > 0 (

İkinci dereceden denklemleri ve eşitsizlikleri parametrelerle çözmenin teorik temelini inceledik. Gerekli formülleri ve dönüşümleri hatırladık, diskriminantın değerine, baş katsayının işaretine, parabolün köklerinin ve köşelerinin konumuna bağlı olarak ikinci dereceden bir fonksiyonun grafiklerinin farklı düzenlemelerine baktık. Sonuçları çözmek ve seçmek için bir şema belirledik ve bir tablo derledik.

Proje ikinci dereceden denklemleri ve eşitsizlikleri çözmek için analitik ve grafiksel yöntemler göstermektedir. Bir meslek okulundaki öğrencilerin materyali daha iyi özümsemeleri için materyalin görsel algısına ihtiyaçları vardır. X değişkeninin nasıl değiştirilebileceği ve parametrenin eşit değer olarak nasıl kabul edilebileceği gösterilir.

Bu konunun net bir şekilde anlaşılması için, her bölüm için 1 – 2 parametreli 8 problemin çözümü ele alınmıştır. 1 numaralı örnekte, çeşitli parametre değerleri için çözümlerin sayısı dikkate alınır; 3 numaralı örnekte ikinci dereceden bir denklemin çözümü, çeşitli başlangıç ​​koşulları altında analiz edilir. İkinci dereceden eşitsizliklerin çözümü için bir grafik çizimi yapılmıştır. 5 numaralı örnekte bir parametrenin eşit değer olarak değiştirilmesi yöntemi kullanılmıştır. Proje, Birleşik Devlet Sınavını geçmeye yönelik yoğun hazırlık için C bölümünde yer alan görevlerden 8 numaralı örneğin dikkate alınmasını içermektedir.

Öğrencilerin parametrelerle ilgili problemleri çözme konusunda yüksek kaliteli eğitimi için, multimedya teknolojilerinin tam olarak kullanılması tavsiye edilir, yani: dersler için sunumlar, elektronik ders kitapları ve kitaplar ve medya kütüphanesinden kendi geliştirmelerinizi kullanın. Matematik + bilgisayar bilimleri ikili dersleri çok etkilidir. İnternet öğretmenler ve öğrenciler için vazgeçilmez bir yardımcıdır. Sunum, mevcut eğitim kaynaklarından içe aktarılmış nesneler gerektirir. Çalışmak için en uygun ve kabul edilebilir olanı “Okulda Microsoft Office Kullanımı” merkezidir.

Bu konuyla ilgili metodolojik önerilerin geliştirilmesi, okula çalışmaya gelen genç öğretmenlerin işini kolaylaştıracak, öğretmen portföyüne eklenecek, özel konularda model oluşturacak ve örnek çözümler, öğrencilerin karmaşık görevlerle baş etmelerine yardımcı olacaktır.

9. Edebiyat.

1. Gornshtein P.I., Polonsky V.B., Yakir M.S. Parametrelerle ilgili sorunlar. “Ilexa”, “Spor Salonu”, Moskova - Kharkov, 2002.

2. Balayan E.N. Birleşik Devlet Sınavı ve Olimpiyatlara hazırlanmak için matematikte bir problemler koleksiyonu. 9-11 sınıflar. "Phoenix", Rostov-na-Donu, 2010.

3. Yastrebinetsky G.A. Parametrelerle ilgili sorunlar. M., "Aydınlanma", 1986.

4. Kolesnikova S.I. Matematik. Birleşik Devlet Sınavının karmaşık problemlerini çözme. M. "IRIS - basın", 2005.

5. Rodionov E.M., Sinyakova S.L. Matematik. Üniversitelere başvuranlar için rehber. Eğitim merkezi "Orientir" MSTU adını almıştır. N.E. Bauman, M., 2004.

6. Skanavi M.I. Üniversitelere girenler için matematik problemlerinin derlemesi: 2 kitapta. Kitap 1, M., 2009.