"Kombinasyonlar" konulu sunum. "Kombinatorik: hareketler, permütasyonlar, kombinasyonlar" konulu cebir ve analiz ilkeleri üzerine bir ders sunumu Tekrarlı kombinasyonlar

“Kombinatorik problemler” - Bir kişi bir kitabı kaç farklı şekilde seçebilir? Bir komutan ve bir mühendisten oluşan bir gemi mürettebatı kaç farklı şekilde oluşturulabilir? Kombinatorik. Problem No. 2. K. Toplama kuralı Çarpma kuralı. Toplama kuralı. Çözüm: 30 + 40 = 70 (bir şekilde). Görev No.1. Sorun 3. I. Komutanlık için üç, mühendislik için de 2 aday olsun.

“Elemanların yerleştirilmesi” - Kombinatorik. Konaklama. Yerleştirme ve kombinasyon. Formüller: n>k olmak üzere herhangi bir n ve k doğal sayısı için eşitlikler geçerlidir: n verisinden iki elemanın seçim sayısı için: Kombinasyon. Kombinatorikte, n'den k'ye kadar olan bir kombinasyon, verilen n elemandan seçilen k eleman kümesidir.

“İstatistiksel özellikler” - Matematiksel istatistikler, vb. İstatistiksel araştırma. 5. İstatistik nedir? 3. 9. Aritmetik ortalama Aralık Modu Medyan. Araştırma faaliyetlerinin aşamaları. 2. 14. “Üç tür yalan vardır: sıradan yalanlar, bariz yalanlar ve istatistiksel yalanlar. "

“Kombinasyonlar” - A, B, C, D harfleri vardır. tüm kombinasyonları yalnızca iki harften yapın. Bağımsız çalışma 2 görevden oluşuyordu. Problem 13 öğrenci tarafından doğru çözülmüş olup örnek 17 öğrencidir. 3 öğrenci çalışmayı tamamlayamadı. Kombinatoryal problemler. Görev No.1. Kaç öğrenci bağımsız çalışmayı başarıyla çözdü? Çalışmayı yazmak için 30 öğrenci gerekti.

“Elementlerin permütasyonları” - Permütasyonların sözlüksel olarak numaralandırılması için doğrudan algoritma. Kombinatorik. En büyük artan alt dizi problemi. Setin numaralandırılması. Algoritmanın resmi açıklaması. Yeniden düzenlemeler. Permütasyonların sözlüksel sayımına ilişkin teorem. Permütasyonların numaralandırılması. Temel transpozisyonlarla permütasyonların numaralandırılması.

“Kombinatorik 9. sınıf” - Toplantının 30 katılımcısı arasından bir başkan ve sekreter seçmesi gerekir. Çözüm: a) 3! = 1 · 2 · 3 =6 b) 5! = 1 · 2 · 3 · 4 · 5 = 120. II. Gösterim: P n Permütasyonların hesaplanması için formül: P n = A6 10 =n ·(n -1) · (n-2) · … · 3 · 2 · 1=n! 2. grup. Tanım: Kombinasyonların hesaplanması için formül: *. Cevaplar ve çözümler. 2. grup.

Konuda toplam 25 sunum bulunmaktadır.

KOMBİNATÖRLER

Dersin Hedefleri:

Kombinatorik çalışmalarının neler olduğunu öğrenin
Kombinatoriklerin nasıl ortaya çıktığını öğrenin
Kombinatorik formüllerini inceleyin ve sorunları çözerken bunları nasıl uygulayacağınızı öğrenin

Kombinatoriğin matematiğin bir dalı olarak doğuşu, Blaise Pascal ve Pierre Fermat'ın kumar teorisi üzerine çalışmalarıyla ilişkilidir.

Blaise Pascal

Pierre Fermat

Kombinatoryal yöntemlerin geliştirilmesine büyük katkı G.V. Leibniz, J. Bernoulli ve L. Euler.

G.V. Leibniz

L. Euler.

J. Bernoulli

Lemma. A kümesinin m elemanı ve B kümesinin n elemanı olsun. O halde a\ A'da, b\ B'de mn olmak üzere tüm farklı (a,b) çiftlerinin sayısı olacaktır. Kanıt. Gerçekte, A kümesindeki bir öğeyle n tane farklı çift oluşturabiliriz ve A kümesinde toplamda m öğe vardır.

Yerleştirmeler, permütasyonlar, kombinasyonlar a,b,c gibi üç elemanlı bir kümemiz olsun. Bu unsurlardan ikisini hangi yollarla seçebiliriz? ab,ac,bc,ba,ca,cb.

Yeniden düzenlemeler Bunları mümkün olan her şekilde yeniden düzenleyeceğiz (nesnelerin sayısı değişmeyecek, yalnızca sıraları değişecek). Ortaya çıkan kombinasyonlara permütasyon denir ve sayıları eşittir Pn = N! =1 · 2 · 3 · ... · ( n-1)n

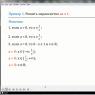
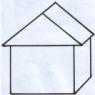
Sembol n! faktöriyel olarak adlandırılır ve 1'den n'ye kadar tüm tam sayıların çarpımını belirtir. Tanım gereği, buna inanılıyor 0!=1 1!=1 Resimde n=3 nesnenin (farklı şekiller) tüm permütasyonlarının bir örneği bulunmaktadır. Formüle göre tam olarak P3=3!=1⋅2⋅3=6 olması gerekir ve olan da budur.

Nesnelerin sayısı arttıkça permütasyonların sayısı da hızla artıyor ve bunları net bir şekilde tasvir etmek zorlaşıyor. Örneğin, 10 öğenin permütasyon sayısı zaten 3628800'dür (3 milyondan fazla!).

Yerleşimler N farklı nesne olsun. Bunlardan m nesne seçeceğiz ve bunları mümkün olan tüm şekillerde yeniden düzenleyeceğiz (yani, seçilen nesnelerin hem kompozisyonu hem de sıraları değişecek). Ortaya çıkan kombinasyonlara n nesnenin m'ye göre yerleşimi denir ve bunların sayısı sabah =n!(n−m)!=n⋅(n−1)⋅...⋅(n−m+1)

Tanım. N farklı elemandan oluşan bir kümeyi m elemana yerleştirerek (m ≤ N) arandı kombinasyonlar Belirli n elementten m elementten oluşan ve elementlerin kendisinde veya elementlerin sıralarında farklılık gösteren.

Kombinasyonlar N farklı nesne olsun. Bunlardan m nesneyi mümkün olan her şekilde seçeceğiz (yani seçilen nesnelerin bileşimi değişir, ancak sıra önemli değildir). Ortaya çıkan kombinasyonlara n nesnenin m kadar kombinasyonu denir ve bunların sayısı Cmn=n!(n−m)!⋅m!

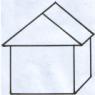
n=3 nesnelerin (farklı şekiller) m=2'ye göre tüm kombinasyonlarının bir örneği aşağıdaki resimdedir. Formüle göre tam olarak C23=3!(3−2)!⋅2!:3!=3 olmalıdır. Her zaman yerleşimlerden daha az kombinasyon olduğu açıktır (çünkü sıralama yerleşimler için önemlidir, ancak kombinasyonlar için değildir) ve özellikle m! kez, yani bağlantı formülü doğrudur: Amn=Cmn⋅Pm.

Yöntem 1. Bir oyuna 2 kişi katılıyor, bu nedenle 15 kişiden 2'sini kaç farklı şekilde seçebileceğinizi hesaplamanız gerekiyor ve bu tür çiftlerdeki sıralama önemli değil. Her biri m elementten oluşan n farklı elementin kombinasyon sayısını (yalnızca bileşimleri farklı olan örnekler) bulmak için formülü kullanalım.

n!= 1⋅ 2 ⋅3⋅...⋅ n , n=2, m=13 ile.

Yöntem 2.İlk oyuncu 14 oyun oynadı (2., 3., 4. vb. 15'e kadar), 2. oyuncu 13 oyun oynadı (3., 4. vb. 15'e kadar). ilk), 3. oyuncu - 12 oyun, 4. - 11 oyun, 5 - 10 oyun, 6 - 9 oyun, 7 - 8 oyun, 8 - 7 oyun,

ve 15'incisi zaten herkesle oynadı.

Toplam: 14+13+12+11+10+9+8+7+6+5+4+3+2+1=105 oyun

CEVAP. 105 oyun.

Matematik öğretmeni Svetlana Valerievna Aksenova

Bugrovskaya ortaokulu, Vsevolozhsk bölgesi, Leningrad bölgesi

Sunum önizlemelerini kullanmak için bir Google hesabı oluşturun ve bu hesaba giriş yapın: https://accounts.google.com

Slayt başlıkları:

Kombinasyonlar

Kombinasyonlar m veriden n elemanın sırası dikkate alınmaksızın yapılan tüm seçimlerin sayısına m elemanın n'ye göre kombinasyon sayısı denir. Tüm kombinasyonlar en az bir öğe açısından birbirinden farklıdır; Burada öğelerin sırası önemli değildir; Kombinasyon ile düzenleme arasındaki fark, bir düzenlemedeki öğeleri yeniden düzenlerseniz farklı bir düzenleme elde etmenizdir, ancak kombinasyon, içinde yer alan öğelerin sırasına bağlı değildir.

Kombinasyonlar m veriden n elemanın sırası dikkate alınmaksızın yapılan tüm seçimlerin sayısına m elemanın n'ye göre kombinasyon sayısı denir. Aranan: 6'dan 3'e kadar olan kombinasyon sayısı: 4'ten 4'e kadar olan kombinasyon sayısı:

Görev No. 1 20 öğrenciden iki görevli memuru seçmeniz gerekir. Bu kaç farklı şekilde yapılabilir? Çözüm: 20 kişiden iki kişiyi seçmemiz gerekiyor. Hiçbir şeyin seçim sırasına bağlı olmadığı açıktır, yani Ivanov - Petrov veya Petrov - Ivanov aynı çift görevli memurdur. Dolayısıyla bunlar 20'ye 2'lik kombinasyonlar olacaktır.

Görev No.2. Minotaur'un labirentte çürüyen 25 mahkumu var. a) Sabah kahvaltısı, öğle yemeği ve akşam yemeği için bunlardan üçünü kaç farklı şekilde seçebilir? b) Üç esiri özgürlüğe salıvermenin kaç yolu vardır? Çözüm: A) Sıra önemlidir. B) Sıra önemli değil

Görev No. 3 Sınıfta 27 öğrenci var, bunlardan üçünün seçilmesi gerekiyor. Aşağıdaki durumlarda bu kaç farklı şekilde yapılabilir: a) birinci öğrenci problemi çözmeli, ikincisi tebeşir almaya gitmeli, üçüncüsü yemek odasında göreve gitmeli; b) koro halinde şarkı söylemeliler mi? 6

Olimpiyatlara katılmak üzere bir matematik kulübünün yedi üyesinden oluşan iki kişilik bir takım kaç farklı şekilde oluşturulabilir? Görev No.4

Görev No. 5 Departmanın 5 lider ve 8 kıdemli çalışanı bulunmaktadır. İki önde gelen ve iki kıdemli araştırmacı bir iş gezisine gönderilmelidir. Bir seçim kaç farklı şekilde yapılabilir?

36 kartlık bir desteden rastgele 4 kart çekiliyor. Çekilen tüm kartların as olma olasılığı nedir? Sorun #6

Sorun No. 7 50 parçadan oluşan bir partide 10 adet kusurlu parça var. Partiden rastgele dört parça alınıyor. 4 parçanın tamamının arızalı olma olasılığını belirleyin. Toplam sonuçlar: Olumlu sonuçlar: Olasılık.

Yeniden düzenlemeler Yerleşimler Kombinasyonlar Olasılık

Belediye eğitim kurumu ortaokul No. 30, Volgograd

Matematik öğretmeni Skleinova N.I.

Faktöriyel

Tanım 1

Faktöriyel ilk n doğal sayının çarpımıdır

N! = 1*2*2*…(n-2)(n-1)n

2!=1*2=2

3!=1*2*3=6

4!= 1*2*3*4=24

5!=1*2*3*4*5=120

Yeniden düzenlemeler

Tanım 2

N elemanın permütasyonu, bu elemanların her birinin belirli bir sıraya göre düzenlenmesidir P=n!

örnek 1

Final yarışındaki 8 katılımcı sekiz koşu bandına kaç farklı şekilde yerleştirilebilir?

R 8 =8!=1*2*3*4*5*6*7*8= 40320(yollar)

Yerleşimler

Tanım 3

N elemanın k (k≤ n) ile düzenlenmesi, verilen n elemandan belirli bir sırayla alınan herhangi bir k elemandan oluşan herhangi bir kümedir

Örnek 2

İkinci sınıf öğrencileri 8 ders çalışıyorlar. Bir gün için 4 farklı konuyu içerecek şekilde bir program kaç farklı şekilde oluşturulabilir?

A 8 4 =8*7*6*5= 1680 (yollar)

A N k =

Kombinasyonlar

Tanım 4

k'nin n elemanından oluşan bir kombinasyon, verilen n elemandan seçilen k elemandan oluşan herhangi bir kümedir

İLE N k =

Örnek 3

Turist grubunun 15 üyesinden üç görevlinin seçilmesi gerekmektedir. Bu seçim kaç farklı şekilde yapılabilir?

İLE 15 3 =15!/(3!*12!)=(13*14*15)/(1*2*3)= 455(yol)

Olasılık

Tanım 5

Bir olayın olasılığı A, bir testin olumlu sonuçlarının N(A) sayısının tüm eşit olası sonuçların N sayısına oranıdır.

P(A)= N(A)/N

Örnek 4

Geometri alanındaki 25 sınav kağıdından öğrenci 11'ini ilk ve 8'ini sonuncu olarak hazırladı. Sınavda kendisinin hazırlamadığı bir bilet alma olasılığı nedir?

P(A)=(25-11-8)/25= 0,24

Olasılıkların eklenmesi

Tanım 6

C olayı, iki uyumsuz olaydan birinin meydana geldiği anlamına geliyorsa: A veya B, bu durumda C olayının olasılığı, A ve B olaylarının olasılıklarının toplamına eşittir.

P(C)=P(A)+P(B)

Zıt olayların olasılıklarının toplamı 1'dir

P(A)+P( A )=1

Olasılıkların Çarpılması

Tanım 7

C olayı, iki bağımsız A ve B olayının ortaklaşa meydana gelmesi anlamına geliyorsa, C olayının olasılığı, A ve B olaylarının olasılıklarının çarpımına eşittir.

P(C)=P(A)*P(B)

Olasılık

Olasılıkların toplamı

İki olayın olasılıklarının toplamı, bu olayların çarpımlarının olasılıkları ile bu olayların toplamının olasılıklarının toplamına eşittir.

P(A)+P(B)= P(A*B) +P(A+B)

Tutarın olasılığı

İki olayın toplamının olasılığı, bu olayların olasılıklarının toplamı ile bu olayların olasılıklarının çarpımı arasındaki farka eşittir.

P(A+B)=P(A)+P(B)-P(A)*P(B)

Sorun 1

Çözüm

Durum

Her birinin olasılığı isabetler eşittir 0,8.

Bir biatloncu hedefe 5 kez atış yapar. Tek atışta hedefi vurma olasılığı 0,8'dir. Biatloncunun hedefleri ilk 3 kez vurması ve son 2 kez kaçırma olasılığını bulun. Sonucu yüzlüğe yuvarlayın.

Her birinin olasılığı kayıp 1-0,8'e eşit= 0,2 .

Olasılık çarpımı formülünü kullanarak şunu elde ederiz:

P(bir )=0,8*0,8*0,8*0,2*0,2

P(bir )= 0,02048 0,02

Cevap: 0,02

Sorun 2

Durum

Çözüm

Masal Ülkesinde iki tür hava vardır: iyi ve mükemmel ve sabah bir kez oluşan hava, gün boyu değişmeden kalır. Yarınki havanın bugünkü ile aynı olacağı 0,6 olasılıkla biliniyor. Bugün 18 Eylül, Masal Diyarı'nda hava güzel. 21 Eylül'de Periler Diyarı'nda havanın güzel olma olasılığını bulun.

18 Eylül'de hava güzel olduğuna göre 19 Eylül'de hava 0,6 olasılıkla iyi, 0,4 olasılıkla mükemmel.

19 Eylül'de hava güzelse, 20 Eylül'de havanın iyi olma olasılığı 0,6*0,6=0,36'dır.

Havanın mükemmel olma olasılığı 0,6*0,4=0,24

Benzer şekilde, 19 Eylül'de hava mükemmelse, 0,4 * 0,6 = 0,24 olasılıkla 20 Eylül'de hava mükemmel olacaktır. 20 Eylül'de havanın güzel olma ihtimali 0,4*0,4=0,16'dır.

Benzer şekilde akıl yürüterek, 21 Eylül'de havanın mükemmel olma olasılığının toplamın olasılığına eşit olacağını buluyoruz: 0,6*0,24+ +0,6*0,24+0,4*0,16+0,6*0,24= 0,496

Sorun 3

Durum

Çözüm

Otomatik bir hat pil üretir. Bitmiş bir pilin arızalı olma olasılığı 0,02'dir. Paketlemeden önce her pil bir kontrol sisteminden geçer. Sistemin arızalı bir pili bloke etme olasılığı 0,98'dir. Sistemin yanlışlıkla çalışan bir pili bloke etme olasılığı 0,03'tür. Rastgele seçilen bir pilin kontrol sistemi tarafından bloke edilme olasılığını bulun.

A = olayı olsun (pil bloke edilecektir), o zaman bu olayın meydana gelme olasılığı olayların kesişimlerinin birleşimi olarak bulunabilir.

P(A)=0,02*0,98+0,98*0,03

P(A)=0,98(0,02+0,03)

P(A)=0,98*0,05= 0,049

Cevap: 0,049

Edebiyat

Makarychev Yu.N. Cebir: istatistik ve olasılık teorisinin unsurları: ders kitabı. genel eğitim öğrencileri için el kitabı. Kurumlar. Yayınevi "Prosveshcheniye", 2003

Mordkovich A.G., Semenov P.V. Cebir ve matematiksel analizin başlangıcı. Bölüm 1. Genel eğitim kuruluşları için ders kitabı. Yayınevi "Mnemosyne", 2015

Lysenko F.F., Kulabukhova S.Yu. Matematik. Birleşik Devlet Sınavı 2016'ya hazırlık. Yayınevi "Legion" LLC, 2015

Vysotsky I.R., Yashchenko I.V. Birleşik Devlet Sınavı 2016. Matematik. Olasılık teorisi. Çalışma kitabı. Yayınevi MCNMO, 2016

1. Organizasyon anı
Öğrencileri selamlamak, dersin konusunu ve amacını anlatmak
2. İşlenen konunun tekrarı ve pekiştirilmesi
· Ödevle ilgili soruların yanıtları (çözülmemiş problemlerin analizi).
· Materyalin asimilasyonunun izlenmesi (yazılı anket).
seçenek 1
1. Güvenilir bir olay ve olasılığı.
2. a) Rastgele bir deneyde iki zar atılıyor. Toplamın 7 puan olma olasılığını bulun. Sonucu yüzlüğe yuvarlayın.
b) Jimnastik şampiyonasına 40 sporcu katılıyor: 12'si Arjantin'den, 9'u Brezilya'dan, geri kalanı Paraguay'dan. Cimnastikçilerin performans sırası kurayla belirlenir. İlk yarışan sporcunun Paraguaylı olma olasılığını bulun.
c) Ortalama olarak satılan 500 bahçe pompasından 4'ünde sızıntı vardır. Kontrol için rastgele seçilen bir pompanın sızıntı yapmama olasılığını bulun.
Seçenek 2
1. İmkansız olay ve olasılığı.
2. a) Rastgele bir deneyde iki zar atılıyor. Toplamın 9 puan olma olasılığını bulun. Sonucu yüzlüğe yuvarlayın.
b) Jimnastik şampiyonasına 64 sporcu katılıyor: 20'si Japonya'dan, 28'i Çin'den, geri kalanı Kore'den. Cimnastikçilerin performans sırası kurayla belirlenir. İlk yarışan sporcunun Koreli olma olasılığını bulun.
c) Fabrika çanta üretiyor. Ortalama olarak her 170 kaliteli poşete karşılık altı adet gizli kusurlu poşet bulunmaktadır. Satın alınan çantanın yüksek kalitede olma olasılığını bulun. Sonucu yüzlüğe yuvarlayın.

Cevap: seçenek 1. 2. a) 0,17; b) 0,475; c) 0,992.
seçenek 2. 2. a) 0,11; b) 0,25; c) 0,97.
3. Yeni materyal öğrenmek
Sınıf, bilgi toplayan, derleyen ve çalışmalarının sonuçlarını sınıfta sunan gruplara bölündü (öğrencilerin çalışmalarının sonuçlarını sunması).
1 grup(Bilim adamlarının ortaya çıkmasının kökeninde olduğu kombinatorik biliminin ortaya çıkmasına hangi faktörlerin (nedenlerin) katkıda bulunduğu hakkında bilgi bulun).
2. grup(Kombinatoriklerin gerçek hayatta var olup olmadığı ve varsa hangi endüstrilerde kullanıldığı hakkında bilgi edinin).

3 grup (Hangi problemlerin kombinatoryal olarak adlandırıldığı ve bunların nasıl çözülebileceği hakkında bilgi edinin, her bir çözüm yöntemini göz önünde bulundurun ve belirli bir yöntemle çözülen çeşitli problemlerden seçim yapın).
3.1. 1 grup.
Çok çeşitli uzmanlıkların temsilcileri, harflerden, rakamlardan ve diğer nesnelerden oluşan belirli kombinasyonları içeren problemleri çözmek zorundadır.
En basit olasılıksal problemleri ele alırken, farklı sonuçların (kombinasyonların) sayısını saymamız gerekiyordu. Az sayıda eleman için bu tür hesaplamaların yapılması kolaydır. Aksi takdirde böyle bir görev ciddi bir zorluk teşkil eder. (slayt 1)

Kombinatorikverilen öğelerden yapılabilecek farklı kombinasyonların (belirli koşulları sağlayan) sayısıyla ilgili soruları inceleyen bir matematik dalıdır.
Kombinatorik- en basit “bağlantıların” incelendiği bir matematik dalı. Permütasyonlar, n nesneden oluşabilen ve sıralarını mümkün olan her şekilde değiştiren bileşiklerdir; yerleşimlerinin sayısı - verilen n sayısından m nesne içeren, nesnelerin sırasına göre veya nesnelerin kendisinde farklılık gösteren bileşikler; sayıları Kombinasyonlar - n üzerinden m öğe içeren, birbirinden en az bir öğe bakımından farklı olan bileşikler (“Büyük Sovyet Ansiklopedisi” tarafından yayınlanan modern açıklayıcı sözlükte).
Tarih öncesi çağlarda insanlar, belirli nesneleri seçmek, bunları belirli bir sıraya koymak ve farklı düzenlemeler arasından en iyisini bulmak, avcılar için av sırasında, savaşçılar için savaş sırasında, aletler için ise en iyi pozisyonu seçmek zorunda kaldıkları sorunlarla karşı karşıya kaldılar. . (slayt 2)

· "Kombinatorik" terimi, 1666'da "Kombinasyon Sanatı Üzerine Söylemler" adlı eserini yayınlayan Leibniz tarafından matematiksel kullanıma kazandırılmıştır. (slayt 3)
· Kombinatorikler ilk olarak ortaya çıktı XVI çeşitli kumar oyunlarının yayılmasıyla bağlantılı olarak. (slayt 4)
…
3.1. 2. grup.(slayt 1)
Kumarın incelenmesiyle başlayan bir bilimin, insan bilgisinin en önemli nesnesi olmayı vaat etmesi dikkat çekicidir. Sonuçta hayattaki soruların çoğu aslında olasılık teorisinden kaynaklanan problemlerdir.
P. Laplace

Kombinatoriklerin uygulama alanları:
. eğitim kurumları (zamanlama) (slayt 2)
. catering endüstrisi (menü planlama)
. dilbilim (harf kombinasyonları için seçenekler dikkate alınarak)
. coğrafya (harita renklendirme) (slayt 3)
…
…
3.1. 3 grup
Belirli nesnelerin birleşimlerini içeren problemlere denir. kombinatoryal.(slayt 1)
Ekleme kuralı: eğer bir A nesnesi seçilebiliyorsa M yollar ve başka bir B nesnesi seçilebilir N o zaman “A ya da B” seçimi yapılabilir m + n yol.
(slayt 2)
Örneğin:
· Bir tabakta 5 elma ve 4 portakal var. Bir meyveyi kaç farklı şekilde seçebilirsiniz?
Problemin koşullarına göre bir elma beş, bir portakal ise dört şekilde seçilebilir. Sorun “ya elma ya da portakal” seçimiyle ilgili olduğundan, toplama kuralına göre bu işlem 5 + 4 = 9 şekilde yapılabilir.
· Şimdi şu soruna bir bakalım: 1,4,7 rakamlarından her biri bir sayıyı yazarken birden fazla kullanılmadan kaç tane iki basamaklı sayı oluşturulabilir? (slayt 3)
· Çözüm: Herhangi bir rakamı kaçırmamak veya tekrarlamamak için artan sırada yazacağız. Önce 1 rakamıyla başlayan, sonra 4 rakamıyla ve son olarak da 7 rakamıyla başlayan sayıları yazıyoruz:
14, 17, 41, 47, 71, 74.
Cevap: 6.
Bu yöntem denir seçeneklerin numaralandırılması. Böylece bu üç rakamdan toplam 6 farklı iki basamaklı sayı oluşturulabilir.
Bu sorun başka bir şekilde çözülebilir. Onun adı - olası seçenekler ağacı. Bu görev için özel bir devre inşa edilmiştir. (slayt 4) (slayt 5)
Bir yıldız işareti koyduk. Olası seçeneklerin sayısını gösterecektir.
Daha sonra yıldız işaretinden 3 bölüm alıyoruz. Problem ifadesinde 1, 4, 7 olmak üzere 3 sayı verilmiştir.
Bu sayıları segmentlerin sonuna koyuyoruz. Belirli bir sayıdaki onlarca sayısını göstereceklerdir.
Daha sonra her sayıdan 2 segment çiziyoruz.
Bu parçaların sonuna da 1, 4, 7 rakamlarını yazıyoruz. Bunlar birlerin sayısını gösterecek.
Elimizdeki sayılara bakalım: 14, 17, 41, 47, 71, 74. Yani toplamda 6 sayımız var.
Cevap: 6.

Bu şema, "baş aşağı" ve gövdesiz de olsa gerçekten bir ağaca benziyor.
Çarpma kuralı: A nesnesi seçilebiliyorsa M ve eğer bu tür her seçimden sonra B nesnesi n şekilde seçilebiliyorsa, o zaman (A, B) çiftinin seçimi belirtilen sırayla gerçekleştirilebilir. m∙ N yollar. (slayt 6)
· 1,4,7 rakamlarından her biri bir defadan fazla kullanılmadan kaç tane iki basamaklı sayı oluşturulabilir?
Bu sorun, olası seçeneklerden oluşan bir ağaç oluşturmadan farklı şekilde ve çok daha hızlı çözülebilir. Şöyle düşünelim. İki basamaklı bir sayının ilk rakamı üç şekilde seçilebilir. İlk rakam seçildikten sonra iki rakam kalacağı için kalan rakamlardan ikinci rakam iki şekilde seçilebilir. Bu nedenle, gerekli üç basamaklı sayıların toplam sayısı 3∙2 çarpımına eşittir, yani. 6.
· 5, 9, 0, 6 sayılarından kaç tane beş basamaklı sayı oluşturulabilir?

Çarpma kuralına göre şunu elde ederiz: 4∙4∙4∙4=256 sayı.
(slayt 7)
Yeniden düzenlemeler -her biri aşağıdakileri içeren bağlantılar N belirli bir sırayla alınan çeşitli unsurlar (slayt 8)
Pn=n! = 1 · 2 · 3 · … · (n -2) · (n -1) · n
Görev.(slayt 9)
Yedi farklı kitap bir rafa kaç farklı şekilde sıralanabilir?
Çözüm:
Bu tür yolların sayısı yedi elementin permütasyon sayısına eşittir,
onlar. P 7 = 7! = 1 · 2 · 3 · … · 7 = 5040.
Cevap: 5040.
Görev.(slayt 10)
Üçü referans kitabı olmak üzere 10 farklı kitap bulunmaktadır. Kaç şekilde
Bu kitapları, tüm referans kitapları yan yana olacak şekilde bir rafa yerleştirmek mümkün müdür?
Çözüm:
Çünkü Referans kitaplarının yan yana olması gerekiyorsa onları tek kitap olarak değerlendireceğiz. Daha sonra 10 kitabı rafa dizmeniz gerekiyor; 3+1=8 kitap. Yapılabilir P 8 yollar. Ortaya çıkan kombinasyonların her biri için yapabileceğiniz P3 dizin yeniden düzenlemeleri.
Bu nedenle, kitapları rafa yerleştirme yollarının sayısı ürüne eşittir:
P 8 P 3 = 8! · 3! = 40320 · 6 =241920.
Cevap: 241920.
…
…