Αλγεβρική και τριγωνομετρική μορφή μιγαδικού αριθμού. Διάλεξη με θέμα: "Τριγωνομετρική μορφή μιγαδικού αριθμού"

Διάλεξη

Τριγωνομετρική μορφή μιγαδικού αριθμού

Σχέδιο

1.Γεωμετρική παράσταση μιγαδικών αριθμών.

2.Τριγωνομετρική σημειογραφία μιγαδικών αριθμών.

3. Ενέργειες σε μιγαδικούς αριθμούς σε τριγωνομετρική μορφή.

Γεωμετρική αναπαράσταση μιγαδικών αριθμών.

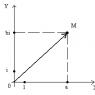
α) Οι μιγαδικοί αριθμοί αντιπροσωπεύονται από σημεία του επιπέδου σύμφωνα με τον ακόλουθο κανόνα: ένα + δι = Μ ( ένα ; σι ) (Εικ. 1).

Εικόνα 1

β) Ένας μιγαδικός αριθμός μπορεί να αναπαρασταθεί ως διάνυσμα που ξεκινά από το σημείοΣΧΕΤΙΚΑ ΜΕ και τελειώνουν σε ένα δεδομένο σημείο (Εικ. 2).

Σχήμα 2

Παράδειγμα 7. Σχεδιάστε σημεία που αντιπροσωπεύουν μιγαδικούς αριθμούς:1; - Εγώ ; - 1 + Εγώ ; 2 – 3 Εγώ (Εικ. 3).

Εικόνα 3

Τριγωνομετρική σημειογραφία μιγαδικών αριθμών.

Μιγαδικός αριθμόςz = ένα + δι μπορεί να ρυθμιστεί χρησιμοποιώντας την ακτίνα - διάνυσμα με συντεταγμένες( ένα ; σι ) (Εικ. 4).

Εικόνα 4

Ορισμός . Διάνυσμα μήκος που αντιπροσωπεύει τον μιγαδικό αριθμόz , ονομάζεται συντελεστής αυτού του αριθμού και συμβολίζεται ήr .

Για οποιονδήποτε μιγαδικό αριθμόz τη μονάδα τουr = | z | καθορίζεται μοναδικά από τον τύπο .

Ορισμός . Η τιμή της γωνίας μεταξύ της θετικής κατεύθυνσης του πραγματικού άξονα και του διανύσματος που αντιπροσωπεύει έναν μιγαδικό αριθμό ονομάζεται όρισμα αυτού του μιγαδικού αριθμού και συμβολίζεταιΕΝΑ rg z ήφ .

Επιχείρημα μιγαδικού αριθμούz = 0 απροσδιόριστο. Επιχείρημα μιγαδικού αριθμούz≠ 0 είναι μια ποσότητα πολλαπλών τιμών και προσδιορίζεται μέχρι τον όρο2πk (k = 0; - 1; 1; - 2; 2; ...): Arg z = αργ z + 2πk , Οπουαργ z - η κύρια τιμή του ορίσματος, που περικλείεται στο διάστημα(-π; π] , αυτό είναι-π < αργ z ≤ π (μερικές φορές η τιμή που ανήκει στο διάστημα λαμβάνεται ως η κύρια τιμή του ορίσματος .

Αυτή η φόρμουλα γιαr =1 συχνά αναφέρεται ως τύπος του De Moivre:

(cos φ + i sin φ) n = cos (nφ) + i sin (nφ), n  N .

Παράδειγμα 11 Υπολογίστε(1 + Εγώ ) 100 .

Ας γράψουμε έναν μιγαδικό αριθμό1 + Εγώ σε τριγωνομετρική μορφή.

a = 1, b = 1 .

cos φ = , αμαρτία φ = , φ = .

(1+i) 100 = [ (συν + αμαρτάνω )] 100 = ( ) 100 (συν 100 + αμαρτω 100) = = 2 50 (cos 25π + i sin 25π) = 2 50 (cos π + i sin π) = - 2 50 .

4) Εξαγωγή της τετραγωνικής ρίζας ενός μιγαδικού αριθμού.

Κατά την εξαγωγή της τετραγωνικής ρίζας ενός μιγαδικού αριθμούένα + δι έχουμε δύο περιπτώσεις:

Ανσι > περίπου , Οτι ;

Ενέργειες σε μιγαδικούς αριθμούς γραμμένες σε αλγεβρική μορφή

Η αλγεβρική μορφή του μιγαδικού αριθμού z =(ένα,σι) ονομάζεται αλγεβρική έκφραση της μορφής

z = ένα + δι.

Αριθμητικές πράξεις σε μιγαδικούς αριθμούς z 1 = α 1 +β 1 ΕγώΚαι z 2 = α 2 +β 2 Εγώ, γραμμένα σε αλγεβρική μορφή, εκτελούνται ως εξής.

1. Άθροισμα (διαφορά) μιγαδικών αριθμών

z 1 ±z 2 = (ένα 1 ± α 2) + (σι 1 ±β 2)∙i,

εκείνοι. η πρόσθεση (αφαίρεση) πραγματοποιείται σύμφωνα με τον κανόνα της πρόσθεσης πολυωνύμων με αναγωγή ομοειδών μελών.

2. Γινόμενο μιγαδικών αριθμών

z 1 ∙z 2 = (ένα 1 ∙α 2 -σι 1 ∙β 2) + (ένα 1 ∙β 2 + α 2 ∙β 1)∙i,

εκείνοι. Ο πολλαπλασιασμός εκτελείται σύμφωνα με τον συνήθη κανόνα για τον πολλαπλασιασμό πολυωνύμων, λαμβάνοντας υπόψη το γεγονός ότι Εγώ 2 = 1.

3. Η διαίρεση δύο μιγαδικών αριθμών γίνεται σύμφωνα με τον ακόλουθο κανόνα:

, (z 2 ≠ 0),

εκείνοι. Η διαίρεση γίνεται πολλαπλασιάζοντας το μέρισμα και ο διαιρέτης με το συζυγές του διαιρέτη.

Η εκτίμηση των μιγαδικών αριθμών ορίζεται ως εξής:

Είναι εύκολο να το δείξεις αυτό

Παραδείγματα.

1. Να βρείτε το άθροισμα των μιγαδικών αριθμών z 1 = 2 – ΕγώΚαι z 2 = – 4 + 3Εγώ.

z 1 +z 2 = (2 + (–1)∙i)+ (–4 + 3Εγώ) = (2 + (–4)) + ((–1) + 3) Εγώ = –2+2Εγώ.

2. Να βρείτε το γινόμενο μιγαδικών αριθμών z 1 = 2 – 3ΕγώΚαι z 2 = –4 + 5Εγώ.

= (2 – 3Εγώ) ∙ (–4 + 5Εγώ) = 2 ∙(–4) + (-4) ∙(–3Εγώ)+ 2∙5Εγώ– 3i∙ 5i = 7+22Εγώ.

3. Βρείτε ιδιωτικό zαπό διαίρεση z 1 \u003d 3 - 2 z 2 = 3 – Εγώ.

z= .

4. Λύστε την εξίσωση: ΧΚαι y Î R.

(2x+y) + (x+y)i = 2 + 3Εγώ.

Δυνάμει της ισότητας των μιγαδικών αριθμών, έχουμε:

που x=–1 , y= 4.

5. Υπολογίστε: Εγώ 2 ,Εγώ 3 ,Εγώ 4 ,Εγώ 5 ,Εγώ 6 ,Εγώ -1 , Εγώ -2 .

6. Υπολογίστε εάν .

.

7. Υπολογίστε το αντίστροφο ενός αριθμού z=3-Εγώ.

Μιγαδικοί αριθμοί σε τριγωνομετρική μορφή

σύνθετο επίπεδοονομάζεται επίπεδο με καρτεσιανές συντεταγμένες ( x, y), αν κάθε σημείο έχει συντεταγμένες ( α, β) εκχωρείται ένας μιγαδικός αριθμός z = a + bi. Στην περίπτωση αυτή καλείται ο άξονας της τετμημένης πραγματικός άξονας, και ο άξονας y είναι φανταστικο. Στη συνέχεια κάθε μιγαδικός αριθμός a+biαναπαριστώνται γεωμετρικά σε επίπεδο ως σημείο Α (α, β) ή διάνυσμα .

Επομένως, η θέση του σημείου ΕΝΑ(και επομένως ο μιγαδικός αριθμός z) μπορεί να οριστεί από το μήκος του διανύσματος | | = rκαι γωνία ιπου σχηματίζεται από το διάνυσμα | | με τη θετική φορά του πραγματικού άξονα. Το μήκος ενός διανύσματος ονομάζεται μέτρο μιγαδικού αριθμούκαι συμβολίζεται με | z|=rκαι η γωνία ιπου ονομάζεται όρισμα μιγαδικού αριθμούκαι συμβολίζεται j = αργζ.

Είναι σαφές ότι | z| ³ 0 και | z | = 0 Û z= 0.

Από το σχ. 2 δείχνει ότι.

Το όρισμα ενός μιγαδικού αριθμού ορίζεται διφορούμενα και μέχρι 2 πκ, κÎ Ζ.

Από το σχ. 2 δείχνει επίσης ότι εάν z=a+biΚαι j=argz,Οτι

cos j =, αμαρτία j =, tg j = .

Αν zОRΚαι z > 0 τότε αργζ = 0 +2πκ;

Αν z ОRΚαι z< 0 τότε argz = p + 2πκ;

Αν z= 0,argzαπροσδιόριστο.

Η κύρια τιμή του ορίσματος προσδιορίζεται στο διάστημα 0 £argz£2 Π,

ή -Π£ arg z £ σελ.

Παραδείγματα:

1. Να βρείτε το μέτρο συντελεστή μιγαδικών αριθμών z 1 = 4 – 3ΕγώΚαι z 2 = –2–2Εγώ.

2. Προσδιορίστε στο μιγαδικό επίπεδο τις περιοχές που καθορίζονται από τις συνθήκες:

1) | z | = 5; 2) | z| 6 £; 3) | z – (2+Εγώ) | 3 £; 4) 6 £ | z – Εγώ| 7 £.

Λύσεις και απαντήσεις:

1) | z| = 5 Û Û είναι η εξίσωση ενός κύκλου με ακτίνα 5 και με κέντρο στην αρχή.

2) Κύκλος με ακτίνα 6 με κέντρο στην αρχή.

3) Κύκλος με ακτίνα 3 με κέντρο σε ένα σημείο z0 = 2 + Εγώ.

4) Ένας δακτύλιος οριοθετημένος από κύκλους με ακτίνες 6 και 7 κεντραρισμένες σε ένα σημείο z 0 = Εγώ.

3. Βρείτε την ενότητα και το όρισμα των αριθμών: 1) ; 2).

1) ; ΕΝΑ = 1, σι = Þ ,

Þ j 1 = .

2) z 2 = –2 – 2Εγώ; α =–2, b=-2 Þ ,

.

Σημείωση: Όταν ορίζετε το κύριο όρισμα, χρησιμοποιήστε το μιγαδικό επίπεδο.

Ετσι: z 1 = .

2) , r 2 = 1, j 2 = , .

3) , r 3 = 1, j 3 = , .

4) , r 4 = 1, j4 = , .

Για να προσδιορίσετε τη θέση ενός σημείου σε ένα επίπεδο, μπορείτε να χρησιμοποιήσετε πολικές συντεταγμένες [g, (p), Οπου σολείναι η απόσταση του σημείου από την αρχή, και (Ρ- η γωνία που κάνει η ακτίνα - το διάνυσμα αυτού του σημείου με τη θετική φορά του άξονα Ω.Θετική φορά αλλαγής γωνίας (Ρθεωρείται αριστερόστροφη φορά. Χρησιμοποιώντας τη σχέση μεταξύ καρτεσιανών και πολικών συντεταγμένων: x \u003d r cos cf, y \u003d r αμαρτία (σελ,

παίρνουμε την τριγωνομετρική μορφή του μιγαδικού αριθμού

z - r(sin (p + i sin

Οπου σολ

Xi + y2, (p είναι το όρισμα ενός μιγαδικού αριθμού, το οποίο βρίσκεται από

l X . y y

ΜΑΘΗΜΑΤΙΚΟΙ τυποι cos(p --, sin^9 ​​= - ή λόγω του γεγονότος ότι tg(p --, (p-arctg

Σημειώστε ότι κατά την επιλογή των τιμών Νυμφεύομαιαπό την τελευταία εξίσωση, είναι απαραίτητο να ληφθούν υπόψη τα σημάδια x και y.

Παράδειγμα 47. Να γράψετε έναν μιγαδικό αριθμό σε τριγωνομετρική μορφή 2 \u003d -1 + l / Z / .

Λύση. Βρείτε το μέτρο και το όρισμα του μιγαδικού αριθμού:

= yj 1 + 3 = 2 . Γωνία Νυμφεύομαιβρείτε από τις σχέσεις cos(σελ = -, sin(p = - .Επειτα

παίρνουμε cos(p = -, σουπ

u/z g~

• - -. Προφανώς, το σημείο z = -1 + V3-/ είναι
• 2 Προς την 3

στο δεύτερο τρίμηνο: (Ρ= 120°

Αντικατάσταση

2 κ.. cos-h; αμαρτία

στον τύπο (1) βρέθηκε 27G L

Σχόλιο. Το όρισμα ενός μιγαδικού αριθμού δεν ορίζεται μοναδικά, αλλά μέχρι έναν όρο που είναι πολλαπλάσιο του 2π.Στη συνέχεια μέσω cn^rορίζω

τιμή ορίσματος που περικλείεται μέσα (σελ 0 %2 Επειτα

Α) ^ r = + 2kk.

Χρησιμοποιώντας τη γνωστή φόρμουλα Euler ε, παίρνουμε την εκθετική μορφή του μιγαδικού αριθμού.

Εχουμε r = r(co^(p + i?, n(p)=re,

Πράξεις σε μιγαδικούς αριθμούς

• 1. Το άθροισμα δύο μιγαδικών αριθμών r, = X] + y x/ και r 2 - x 2 + y 2 / προσδιορίζεται σύμφωνα με τον τύπο r! +2 2 = (x, +^2) + (^1 + ^2)' ζ
• 2. Ως πράξη αφαίρεσης μιγαδικών αριθμών ορίζεται η αντίστροφη προς την πρόσθεση πράξη. Μιγαδικός αριθμός g \u003d g x - g 2,Αν g 2 + g \u003d g x,

είναι η διαφορά των μιγαδικών αριθμών 2, και g 2 .Τότε r = (x, - x 2) + (y, - στο 2) /.

• 3. Γινόμενο δύο μιγαδικών αριθμών g x= x, +y, -z και 2 2 = x 2+ U2Το g καθορίζεται από τον τύπο
• *1*2 =(* +U"0(Χ 2+ Τ 2 -0= X 1 X 2 Y 1 2 -1 + x Υ2 " * + Στο1 Στο2 " ^ =

\u003d (xx 2 ~ YY 2) + ( X Y2 + X 2Y) - "-

Συγκεκριμένα, ε-εε\u003d (x + y-g) (x-y /) \u003d x 2 + y 2.

Μπορείτε να πάρετε τους τύπους πολλαπλασιασμού για μιγαδικούς αριθμούς σε εκθετικές και τριγωνομετρικές μορφές. Εχουμε:

• 1^ 2 - r x e 1 = )Г 2 e > = Г]Г 2 cOs((P + cp2) + ισίνη
• 4. Η διαίρεση μιγαδικών αριθμών ορίζεται ως η αντίστροφη πράξη

πολλαπλασιασμός, δηλ. αριθμός ΣΟΛ--λέγεται πηλίκο της διαίρεσης του r! στο g 2,

Αν r x -1 2 ? 2 . Επειτα

Χ + Τι _ (*і + ІU 2 ~ 1 U2 ) x 2 + ІУ2 (2 + ^Y 2)( 2 ~ 1 Y 2)

x, x 2 + /y, x 2 - ix x y 2 - i 2 y x y 2 (x x x 2 + y x y 2)+ /(- x, y 2 + X 2 Y])

2 2 x 2 + Y 2

1 μι

i(r g

• - 1U e "(1 Fg) - I.sOї ((P - cf 1) + I- (Ρ-,)] >2 >2
• 5. Η αύξηση ενός μιγαδικού αριθμού σε θετική ακέραια ισχύ γίνεται καλύτερα εάν ο αριθμός είναι γραμμένος με εκθετικές ή τριγωνομετρικές μορφές.

Πράγματι, αν z = ge 1 τότε

=(ge,) = r p e t = ΣΟΛ"(συν 8 psr + іt gcr).

Φόρμουλα ζ" =r n (cosn(p+είναι n(p)ονομάζεται τύπος του De Moivre.

6. Εξαγωγή της ρίζας Π-Η ισχύς ενός μιγαδικού αριθμού ορίζεται ως η αντίστροφη πράξη της εκθέσεως p, p- 1,2,3,... δηλ. μιγαδικός αριθμός = y[gπου ονομάζεται η ρίζα Π-ο βαθμός ενός μιγαδικού αριθμού

δ αν σολ = g x. Από αυτόν τον ορισμό προκύπτει ότι g - g", ΕΝΑ g x= l/g. (p-psr x,ΕΝΑ sr^-sr/n, που προκύπτει από τον τύπο Moivre που γράφτηκε για τον αριθμό = r/*+ ippp(p).

Όπως σημειώθηκε παραπάνω, το όρισμα ενός μιγαδικού αριθμού δεν ορίζεται μοναδικά, αλλά μέχρι έναν όρο που είναι πολλαπλάσιο του 2 και.Να γιατί = (p + 2 τμχ, και το όρισμα του αριθμού r, ανάλογα με Προς την,δείχνω (σελ. έωςκαι μπου

dem υπολογισμός με τύπο (σελ. έως= - + . Είναι σαφές ότι υπάρχει Π com-

αριθμοί plex, Πη δύναμη του οποίου είναι ίση με τον αριθμό 2. Οι αριθμοί αυτοί έχουν ένα

και την ίδια ενότητα, ίση με ε[ρ,και τα επιχειρήματα αυτών των αριθμών λαμβάνονται από Προς την = 0, 1, Π - 1. Έτσι, σε τριγωνομετρική μορφή, η ρίζα του i-ου βαθμού υπολογίζεται με τον τύπο:

(p + 2kp . . cf + 2kp

, Προς την = 0, 1, 77-1,

.(p+2kg

και σε εκθετική μορφή - σύμφωνα με τον τύπο l[r - y[ge n

Παράδειγμα 48. Εκτελέστε πράξεις σε μιγαδικούς αριθμούς σε αλγεβρική μορφή:

α) (1- / H / 2) 3 (3 + /)

• (1 - /l/2) 3 (s + /) \u003d (1 - Zl / 2 / + 6 / 2 - 2 l / 2 / ? 3) (3 + /) \u003d
• (1 - Zl/2/ - 6 + 2l/2/DZ + /)=(- 5 - l/2/DZ + /) =

15-Zl/2/-5/-l/2/ 2 = -15 - Zl/2/-5/+ l/2 = (-15 + l/2)-(5 + Zl/2)/;

Παράδειγμα 49. Ανεβάστε τον αριθμό r \u003d Uz - / στην πέμπτη δύναμη.

Λύση. Παίρνουμε την τριγωνομετρική μορφή γραφής του αριθμού r.

G = l/3 + 1 =2, CO8 (p --, 5ІІ7 (Ρ =

• (1 - 2/X2 + /)
• (μικρό-,)

Ο - 2.-x2 + ο

• 12+ 4/-9/
• 2 +і - 4/ - 2/ 2 2 - 3/ + 2 4 - 3/ 3 + і
• (έτσι κι έτσι

Z/ 2 12-51 + 3 15 - 5/

• (3-i) 'з+/
• 9 + 1 s_±.
• 5 2 1 "

Από εδώ Ο--, ΕΝΑ r = 2

Moivre παίρνουμε: i-2

/ ^ _ 7r, . ?ΣΟΛ

• -ΜΑΣ-- IBIP -

• --σι/-

\u003d - (l / W + g) \u003d -2.

Παράδειγμα 50 Βρείτε όλες τις τιμές

Λύση, r = 2, α Νυμφεύομαιβρείτε από την εξίσωση coy(p = -, zt--.

Αυτό το σημείο 1 - /d/z είναι στο τέταρτο τρίμηνο, δηλ. f =--. Επειτα

• 1 - 2
• ( ( UG L

Οι τιμές ρίζας βρίσκονται από την έκφραση

V1 - /l/s = l/2

• --+ 2A:/g ---b 2 κκ
• 3 . . 3

С08--1- και 81П-

Στο Προς την - 0 έχουμε 2 0 = l/2

Μπορείτε να βρείτε τις τιμές της ρίζας του αριθμού 2 παρουσιάζοντας τον αριθμό στην οθόνη

-* ΠΡΟΣ ΤΗΝ/ 3 + 2 τάξη

Στο Προς την= 1 έχουμε μια ακόμη ρίζα:

• 7G. 7G_
• ---b27g ---b2;g
• 3 . . η

7G . . 7G L-C05- + 181P - 6 6

• --Ν-

με? - 7G + / 5Sh - I "

l/3__t_

μορφή σώματος. Επειδή r= 2, α Νυμφεύομαι= , τότε r = 2е 3, και y[g = ε/2ε 2