Санамсаргүй хэмжигдэхүүний математик хүлээлт. Магадлалын онолын үндэс
2. Магадлалын онолын үндэс
Хүлээгдэж буй үнэ цэнэ
Тоон утгатай санамсаргүй хэмжигдэхүүнийг авч үзье. Энэ функцтэй тоог "дундаж утга" эсвэл тэдний хэлснээр "дундаж утга", "төв чиг хандлагын үзүүлэлт" -тэй холбох нь ихэвчлэн ашигтай байдаг. Дараах зүйлд тодорхой болох хэд хэдэн шалтгааны улмаас дундаж утгыг дундаж утга болгон ашиглах нь түгээмэл байдаг.
Тодорхойлолт 3.Санамсаргүй хэмжигдэхүүний математик хүлээлт Xдугаар дуудсан
тэдгээр. Санамсаргүй хэмжигдэхүүний математик хүлээлт нь харгалзах анхан шатны үйл явдлын магадлалтай тэнцүү жинтэй санамсаргүй хэмжигдэхүүний утгуудын жигнэсэн нийлбэр юм.
Жишээ 6Шооны дээд талд унасан тооны математик хүлээлтийг тооцоолъё. Энэ нь 3-р тодорхойлолтоос шууд гардаг
Мэдэгдэл 2.Санамсаргүй хэмжигдэхүүнийг үзье Xүнэт зүйлсийг авдаг x 1, x 2, ..., xм. Дараа нь тэгш байдал
![]() (5)
(5)
тэдгээр. Санамсаргүй хэмжигдэхүүний математик хүлээлт нь санамсаргүй хэмжигдэхүүн тодорхой утгыг авах магадлалтай тэнцүү жинтэй санамсаргүй хэмжигдэхүүний утгуудын жигнэсэн нийлбэр юм.
Дүгнэлт нь анхан шатны үйл явдлууд дээр шууд хийгддэг (4)-ээс ялгаатай нь санамсаргүй үйл явдал нь хэд хэдэн энгийн үйл явдлуудаас бүрдэж болно.
Заримдаа (5) хамаарлыг математикийн хүлээлтийн тодорхойлолт болгон авдаг. Гэсэн хэдий ч доор үзүүлсэн 3-р тодорхойлолтыг ашиглан бодит үзэгдлийн магадлалын загварыг бий болгоход шаардлагатай математик хүлээлтийн шинж чанарыг тогтоох нь хамаарлыг (5) ашиглахаас илүү хялбар байдаг.
(5) хамаарлыг батлахын тулд бид санамсаргүй хэмжигдэхүүний ижил утгатай (4) нөхцөлөөр бүлэглэнэ.

Тогтмол хүчин зүйлийг нийлбэрийн тэмдгээс гаргаж авах боломжтой тул
Үйл явдлын магадлалын тодорхойлолтоор
![]()
Сүүлийн хоёр харилцааны тусламжтайгаар бид хүссэн зүйлийг олж авдаг.

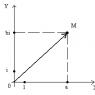
Магадлал-статистикийн онол дахь математикийн хүлээлтийн тухай ойлголт нь механик дахь хүндийн төвийн тухай ойлголттой нийцдэг. Үүнийг цэгүүдэд оруулъя x 1, x 2, ..., xммассын тоон тэнхлэг дээр П(X= x 1 ), П(X= x 2 ),…, П(X= х м) тус тус. Дараа нь тэгш байдал (5) нь энэхүү материаллаг цэгүүдийн системийн хүндийн төв нь математикийн хүлээлттэй давхцаж байгааг харуулж байгаа бөгөөд энэ нь 3-р тодорхойлолтын байгалийн байдлыг харуулж байна.
Мэдэгдэл 3.Болъё X- санамсаргүй утга, М(X)түүний математик хүлээлт, А- хэдэн тоо. Дараа нь
1) M(a)=a; 2) M(X-M(X))=0; 3 сая[(X- а) 2 ]= М[(X- М(X)) 2 ]+(а- М(X)) 2 .
Үүнийг батлахын тулд бид эхлээд тогтмол байдаг санамсаргүй хэмжигдэхүүнийг авч үзэх болно, өөрөөр хэлбэл. функц нь энгийн үйл явдлын орон зайг нэг цэгт буулгадаг А. Тогтмол хүчин зүйлийг нийлбэрийн тэмдгээс гаргаж авах боломжтой тул
Хэрэв нийлбэрийн гишүүн бүрийг хоёр гишүүнд хуваасан бол бүхэл нийлбэр нь мөн хоёр нийлбэрт хуваагдах бөгөөд эхнийх нь эхний гишүүн, хоёр дахь нь хоёр дахь гишүүнээс бүрдэнэ. Иймд хоёр санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт X+Y, анхан шатны үйл явдлын ижил орон зайд тодорхойлсон нь математикийн хүлээлтийн нийлбэртэй тэнцүү байна М(X)Тэгээд М(U)Эдгээр санамсаргүй хэмжигдэхүүнүүд:
M(X+Y) = M(X) + M(Y).
Тиймээс М(X-M(X)) = М(Х) - М(М(Х)).Дээр үзүүлсэн шиг, М(М(X)) = M(X).Тиймээс, М(Х-М(Х)) = М(Х) - М(Х) = 0.
Учир нь (X - a) 2 = ((X – М(X)) + (М(X) - а)} 2 = (X - М(X)) 2 + 2(X - М(X))(М(X) - а) + (М(X) – а) 2 , Тэр М[(X - a) 2] =М(X - М(X)) 2 + М{2(X - М(X))(М(X) - а)} + М[(М(X) – а) 2 ]. Сүүлийн тэгш байдлыг хялбаршуулж үзье. Санал 3-ын нотолгооны эхэнд харуулсанчлан тогтмолын хүлээлт нь өөрөө тогтмол байдаг тул М[(М(X) – а) 2 ] = (М(X) – а) 2 . Тогтмол хүчин зүйлийг нийлбэрийн тэмдгээс гаргаж авах боломжтой тул М{2(X - М(X))(М(X) - а)} = 2(М(X) - а)М(X - М(X)). Сүүлийн тэгшитгэлийн баруун гар тал нь 0 байна, учир нь дээр үзүүлсэн шиг, M(X-M(X))=0.Тиймээс, М[(X- а) 2 ]= М[(X- М(X)) 2 ]+(а- М(X)) 2 нотлох ёстой байсан.
Ярьсан зүйлээс харахад ийм байна М[(X- а) 2 ] хамгийн багадаа хүрдэг Атэнцүү М[(X- М(X)) 2 ], цагт a = M(X),тэгш байдлын хоёр дахь гишүүн учраас 3) үргэлж сөрөг биш бөгөөд зөвхөн заасан утгын хувьд 0-тэй тэнцүү байна А.
Мэдэгдэл 4.Санамсаргүй хэмжигдэхүүнийг үзье Xүнэт зүйлсийг авдаг x 1, x 2, ..., xм, ба f нь тоон аргументын зарим функц юм. Дараа нь
![]()
Үүнийг батлахын тулд математикийн хүлээлтийг тодорхойлдог тэгш байдлын (4) баруун талд ижил утгатай нэр томъёог бүлэглэе.

Тогтмол хүчин зүйлийг нийлбэрийн тэмдгээс хасаж, санамсаргүй үйл явдлын магадлалыг (2) тодорхойлох замаар бид олж авна.
Q.E.D.
Мэдэгдэл 5.Болъё XТэгээд Atэнгийн үйл явдлын ижил орон зайд тодорхойлогдсон санамсаргүй хэмжигдэхүүнүүд, АТэгээд б- зарим тоо. Дараа нь М(aX+ bY)= AM(X)+ бМ(Ю).
Математикийн хүлээлтийн тодорхойлолт ба нийлбэрийн тэмдгийн шинж чанарыг ашиглан бид тэгш байдлын гинжин хэлхээг олж авна.

Шаардлагатай нь батлагдсан.
Дээрх нь математикийн хүлээлт нь өөр гарал үүсэл болон өөр хэмжлийн нэгж рүү (шилжилт) шилжихээс хэрхэн хамаардаг болохыг харуулж байна. Ю=aX+б), түүнчлэн санамсаргүй хэмжигдэхүүний функцүүдэд. Хүлээн авсан үр дүнг техник, эдийн засгийн шинжилгээнд, аж ахуйн нэгжийн санхүү, эдийн засгийн үйл ажиллагааг үнэлэх, гадаад эдийн засгийн төлбөр тооцоонд нэг валютаас нөгөөд шилжих, зохицуулалтын болон техникийн баримт бичигт байнга ашигладаг. авч үзсэн үр дүн нь янз бүрийн масштаб, ээлжийн параметрүүдэд ижил тооцооны томъёог ашиглах боломжийг олгодог.
| Өмнөх |
Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт нь түүний бүх боломжит утгууд ба тэдгээрийн магадлалын бүтээгдэхүүний нийлбэр юм.
Санамсаргүй хэмжигдэхүүн нь зөвхөн магадлалыг нь тэнцүү авч болно.Тэгвэл санамсаргүй хэмжигдэхүүний математик хүлээлт тэгшитгэлээр тодорхойлогдоно.
Хэрэв салангид санамсаргүй хэмжигдэхүүн нь боломжтой утгуудын тоолж болох олонлогийг авдаг бол
Түүгээр ч барахгүй тэгш байдлын баруун талд байгаа цувралууд туйлын нийлбэл математикийн хүлээлт бий болно.
Сэтгэгдэл. Тодорхойлолтоос харахад салангид санамсаргүй хэмжигдэхүүний математик хүлээлт нь санамсаргүй (тогтмол) хэмжигдэхүүн юм.
Ерөнхий тохиолдолд математикийн хүлээлтийн тодорхойлолт
Тархалт нь салангид байх албагүй санамсаргүй хэмжигдэхүүний математик хүлээлтийг тодорхойлъё. Сөрөг бус санамсаргүй хэмжигдэхүүнүүдийн тохиолдлоос эхэлье. Ийм санамсаргүй хэмжигдэхүүнийг математикийн хүлээлт нь аль хэдийн тодорхойлогдсон дискрет хэмжигдэхүүнүүдийн тусламжтайгаар ойртуулж, математик хүлээлтийг түүнд ойртсон дискрет санамсаргүй хэмжигдэхүүнүүдийн математик хүлээлтийн хязгаартай тэнцүү болгох санаа юм. Дашрамд хэлэхэд, энэ нь маш хэрэгтэй ерөнхий санаа бөгөөд энэ нь эхлээд энгийн объектуудын хувьд зарим шинж чанарыг тодорхойлж, дараа нь илүү төвөгтэй объектуудын хувьд тэдгээрийг энгийн зүйлтэй ойртуулах замаар тодорхойлдог.
Лемма 1. Дурын сөрөг бус санамсаргүй хэмжигдэхүүн байг. Дараа нь салангид санамсаргүй хэмжигдэхүүнүүдийн дараалал байдаг

Баталгаа. Хагас тэнхлэгийг уртын тэнцүү хэсгүүдэд хувааж тодорхойлъё
Дараа нь 1 ба 2-р шинж чанарууд нь санамсаргүй хэмжигдэхүүний тодорхойлолтоос амархан дагалддаг ба
Лемма 2. Сөрөг бус санамсаргүй хэмжигдэхүүн ба Лемма 1-ээс 1-3 шинж чанартай салангид санамсаргүй хэмжигдэхүүний хоёр дараалал.
Баталгаа. Сөрөг бус санамсаргүй хэмжигдэхүүнийг бид зөвшөөрдөг гэдгийг анхаарна уу
3-р шинж чанараар эерэг тоонуудын дараалал байгааг харахад хялбар байдаг
Тиймээс үүнийг дагадаг
Дискрет санамсаргүй хэмжигдэхүүнүүдийн математик хүлээлтийн шинж чанарыг ашиглан бид олж авна
Бид Лемма 2-ын баталгааг олж авснаар хязгаарт хүрч байна.
Тодорхойлолт 1. Сөрөг бус санамсаргүй хэмжигдэхүүн, Лемма 1-ээс 1-3 шинж чанартай салангид санамсаргүй хэмжигдэхүүнүүдийн дараалал байя. Санамсаргүй хэмжигдэхүүний математик хүлээлт нь тоо юм.
Лемма 2 нь ойролцоо дарааллын сонголтоос хамаарахгүй гэдгийг баталгаажуулдаг.
Одоо дурын санамсаргүй хэмжигдэхүүн байцгаая. Тодорхойлъё


Тодорхойлолтоос харахад амархан

Тодорхойлолт 2. Дурын санамсаргүй хэмжигдэхүүний математик хүлээлт нь тоо юм
Хэрэв энэ тэгшитгэлийн баруун талд байгаа тоонуудын ядаж нэг нь төгсгөлтэй байвал.
Хүлээгдэж буй шинж чанарууд
Өмч 1. Тогтмол утгын математик хүлээлт нь тогтмолтой тэнцүү байна:
Баталгаа. Бид тогтмолыг нэг боломжит утгатай, магадлалаар авдаг салангид санамсаргүй хэмжигдэхүүн гэж үзэх болно.
Тайлбар 1. Тогтмол утгын үржвэрийг дискрет санамсаргүй хэмжигдэхүүн гэж тодорхойлдог бөгөөд боломжит утгууд нь тогтмол утгын үржвэртэй тэнцүү байна; боломжит утгуудын магадлал нь харгалзах боломжит утгуудын магадлалтай тэнцүү байна.Жишээ нь, хэрэв боломжит утгын магадлал тэнцүү бол тухайн утгыг авах магадлал нь мөн тэнцүү байна.
Үл хөдлөх хөрөнгө 2. Хүлээлтийн тэмдгээс тогтмол хүчин зүйлийг гаргаж болно.
Баталгаа. Санамсаргүй хэмжигдэхүүнийг магадлалын тархалтын хуулиар өгье.
Тайлбар 1-ийг харгалзан бид санамсаргүй хэмжигдэхүүний тархалтын хуулийг бичнэ
Тайлбар 2. Дараагийн шинж чанарт шилжихийн өмнө тэдгээрийн аль нэгнийх нь тархалтын хууль нь нөгөө хувьсагч ямар боломжит утгыг авсанаас хамаарахгүй бол хоёр санамсаргүй хэмжигдэхүүнийг бие даасан гэж нэрлэнэ. Үгүй бол санамсаргүй хэмжигдэхүүнүүд хамааралтай болно. Хэд хэдэн санамсаргүй хэмжигдэхүүнийг бие биенээсээ хамааралгүй хэмжигдэхүүн гэж нэрлэдэг бөгөөд хэрэв тэдгээрийн аль нэг тооны тархалтын хууль нь бусад хувьсагчид ямар боломжит утгуудаас хамаарахгүй бол.
Тайлбар 3. Бид бие даасан санамсаргүй хэмжигдэхүүнүүдийн үржвэрийг тодорхойлдог бөгөөд тэдгээрийн боломжит утгууд нь боломжит утга тус бүрийн үржвэрүүдтэй тэнцүү бөгөөд тухайн бүтээгдэхүүний боломжит утгуудын магадлалын үржвэрүүдтэй тэнцүү байна. Жишээлбэл, хэрэв боломжит утгын магадлал бол боломжит утгын магадлал бол боломжит утгын магадлал юм.
Өмч 3. Хоёр бие даасан санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдгээрийн математик хүлээлтийн үржвэртэй тэнцүү байна.
Баталгаа. Бие даасан санамсаргүй хэмжигдэхүүнийг магадлалын тархалтын хуулиар өгөгдье.
Санамсаргүй хэмжигдэхүүний авч болох бүх утгыг бүрдүүлье.Үүний тулд бүх боломжит утгыг боломжит утга тус бүрээр үржүүлнэ; Үүний үр дүнд бид олж авсан бөгөөд Тайлбар 3-ыг харгалзан бид бүтээгдэхүүний бүх боломжит утгууд өөр байна гэж энгийнээр тооцож түгээлтийн хуулийг бичдэг (хэрэв тийм биш бол нотлох баримтыг ижил төстэй байдлаар гүйцэтгэнэ):
Математикийн хүлээлт нь бүх боломжит утгууд ба тэдгээрийн магадлалын бүтээгдэхүүний нийлбэртэй тэнцүү байна.
Үр дагавар. Хэд хэдэн харилцан бие даасан санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдний математик хүлээлтийн үржвэртэй тэнцүү байна.
Өмч 4. Хоёр санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэр томъёоны математик хүлээлтийн нийлбэртэй тэнцүү байна.
Баталгаа. Санамсаргүй хэмжигдэхүүнийг дараах тархалтын хуулиар өгөгдье.
Хэмжигдэхүүний бүх боломжит утгыг бүрдүүлэх Үүнийг хийхийн тулд боломжит утга тус бүрийг боломжит утга болгон нэмнэ; Бид энгийн байх үүднээс эдгээр боломжит утгууд өөр байна гэж бодъё (хэрэв тийм биш бол нотлох баримт нь ижил төстэй байдлаар хийгддэг), бид тэдгээрийн магадлалыг тус тусад нь тэмдэглэнэ.
Утгын математикийн хүлээлт нь боломжит утгуудын үржвэрийн нийлбэрийг магадлалаар нь тэнцүү байна.
Утга авахаас бүрдэх (энэ үйл явдлын магадлал тэнцүү) үйл явдал нь утгыг авах эсвэл (энэ үйл явдлын магадлал нь нэмэх теоремоор тэнцүү) үйл явдлыг дагуулдаг болохыг баталцгаая. Эндээс "Тэгш байдал" гэсэн үг гарч байна
Эдгээр тэгш байдлын зөв хэсгийг (*) харьцаанд орлуулснаар бид олж авна
эсвэл эцэст нь
Тархалт ба стандарт хазайлт
Практикт санамсаргүй хэмжигдэхүүний боломжит утгуудын дундаж утгын ойролцоо тархалтыг тооцоолох шаардлагатай байдаг. Жишээлбэл, их бууны буудлагад сумнууд онох ёстой бай руу хэр ойрхон унахыг мэдэх нь чухал юм.
Эхлээд харахад тархалтыг тооцоолох хамгийн хялбар арга бол санамсаргүй хэмжигдэхүүний хазайлтын бүх боломжит утгыг тооцоолж, дараа нь тэдгээрийн дундаж утгыг олох явдал юм. Гэсэн хэдий ч энэ зам нь юу ч өгөхгүй, учир нь хазайлтын дундаж утга, өөрөөр хэлбэл. дурын санамсаргүй хэмжигдэхүүний хувьд тэг байна. Энэ өмч нь зарим боломжит хазайлт эерэг, бусад нь сөрөг байдагтай холбон тайлбарладаг; тэдгээрийг харилцан цуцалсны үр дүнд хазайлтын дундаж утга тэг байна. Эдгээр бодол нь боломжит хазайлтыг үнэмлэхүй утга эсвэл квадратаар нь солих нь зүйтэй болохыг харуулж байна. Тэд үүнийг практик дээр ингэж хийдэг. Үнэн бол боломжит хазайлтыг үнэмлэхүй утгаараа сольсон тохиолдолд үнэмлэхүй утгуудтай ажиллах шаардлагатай бөгөөд энэ нь заримдаа ноцтой хүндрэлд хүргэдэг. Тиймээс ихэнхдээ тэд өөр замаар явдаг, жишээлбэл. вариац гэж нэрлэгддэг квадрат хазайлтын дундаж утгыг тооцоол.
Мөн бие даасан шийдлийн даалгавар байх бөгөөд та хариултыг нь харж болно.
Математикийн хүлээлт ба дисперс нь санамсаргүй хэмжигдэхүүний хамгийн түгээмэл хэрэглэгддэг тоон шинж чанар юм. Эдгээр нь тархалтын хамгийн чухал шинж чанаруудыг тодорхойлдог: түүний байрлал, тархалтын зэрэг. Математикийн хүлээлтийг ихэвчлэн дундаж гэж нэрлэдэг. санамсаргүй хувьсагч. Санамсаргүй хэмжигдэхүүний тархалт - тархалтын шинж чанар, санамсаргүй хэмжигдэхүүний тархалт түүний математик хүлээлтийн эргэн тойронд.
Практикийн олон асуудалд санамсаргүй хэмжигдэхүүн - тархалтын хуулийг бүрэн, бүрэн тайлбарлах боломжгүй, эсвэл огт хэрэггүй болно. Эдгээр тохиолдолд тэдгээр нь тоон шинж чанарыг ашиглан санамсаргүй хэмжигдэхүүний ойролцоо тодорхойлолтоор хязгаарлагддаг.
Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт
Математикийн хүлээлтийн тухай ойлголт руу орцгооё. Зарим бодисын массыг x тэнхлэгийн цэгүүдийн хооронд тараацгаая x1 , x 2 , ..., x n. Түүнээс гадна, материаллаг цэг бүр нь магадлал бүхий түүнд тохирох масстай байдаг х1 , х 2 , ..., х n. Материалын цэгүүдийн бүхэл системийн байрлалыг тэдгээрийн массыг харгалзан тодорхойлдог x тэнхлэг дээр нэг цэгийг сонгох шаардлагатай. Материаллаг цэгүүдийн системийн массын төвийг ийм цэг болгон авах нь зүйн хэрэг юм. Энэ нь санамсаргүй хэмжигдэхүүний жигнэсэн дундаж юм X, үүнд цэг бүрийн абсцисса xбихаргалзах магадлалтай тэнцэх "жин"-ээр ордог. Ийнхүү олж авсан санамсаргүй хэмжигдэхүүний дундаж утга Xтүүний математик хүлээлт гэж нэрлэдэг.
Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт нь түүний бүх боломжит утгуудын үржвэрийн нийлбэр ба эдгээр утгуудын магадлал юм.
Жишээ 1Хож-хож сугалаа зохион байгууллаа. 1000 хожил байгаа бөгөөд 400 нь тус бүр 10 рубль юм. Тус бүр нь 300-20 рубль Тус бүр нь 200-100 рубль. тус бүр 100 - 200 рубль байна. Нэг тасалбар авсан хүн дунджаар хэдэн төгрөгийн хожил авах вэ?
Шийдэл. 10*400 + 20*300 + 100*200 + 200*100 = 50,000 рубльтэй тэнцэх нийт хожлын дүнг 1000-д (хожлын нийт дүн) хуваасан тохиолдолд бид дундаж ялалтыг олох болно. Дараа нь бид 50000/1000 = 50 рубль авна. Гэхдээ дундаж ашгийг тооцоолох илэрхийллийг дараахь хэлбэрээр илэрхийлж болно.

Нөгөөтэйгүүр, эдгээр нөхцөлд хожлын хэмжээ нь 10, 20, 100, 200 рублийн утгыг авах боломжтой санамсаргүй хэмжигдэхүүн юм. магадлал нь 0.4-тэй тэнцүү; 0.3; 0.2; 0.1. Тиймээс хүлээгдэж буй дундаж өгөөж нь өгөөжийн хэмжээ ба түүнийг хүлээн авах магадлалын бүтээгдэхүүний нийлбэртэй тэнцүү байна.
Жишээ 2Хэвлэлийн газар шинэ ном гаргахаар шийджээ. Тэр номоо 280 рублиэр зарах гэж байгаа бөгөөд үүнээс 200-г нь өөрт нь, 50-г нь номын дэлгүүрт, 30-ыг нь зохиолчид өгөх юм байна. Хүснэгтэд ном хэвлэх зардал, номыг тодорхой тооны хувь борлуулах магадлалын талаархи мэдээллийг өгсөн болно.
Нийтлэгчийн хүлээгдэж буй ашгийг олоорой.
Шийдэл. Санамсаргүй хэмжигдэхүүн "ашиг" нь борлуулалтаас олсон орлого ба зардлын зардлын зөрүүтэй тэнцүү байна. Жишээлбэл, хэрэв 500 хувь ном зарагдсан бол борлуулалтын орлого нь 200 * 500 = 100,000, хэвлэх зардал нь 225,000 рубль болно. Тиймээс нийтлэгч 125,000 рублийн алдагдал хүлээж байна. Дараахь хүснэгтэд санамсаргүй хэмжигдэхүүний хүлээгдэж буй утгуудыг нэгтгэн харуулав - ашиг.
| Тоо | Ашиг xби | Магадлал хби | xби хби |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Нийт: | 1,00 | 25000 |
Тиймээс бид нийтлэгчийн ашгийн математикийн хүлээлтийг олж авдаг.
![]() .
.
Жишээ 3Нэг цохилтоор цохих боломж х= 0.2. 5-тай тэнцэх тооны цохилтын математик хүлээлтийг хангах бүрхүүлийн хэрэглээг тодорхойл.
Шийдэл. Бидний өнөөг хүртэл хэрэглэж байсан хүлээлтийн томъёоноос бид илэрхийлж байна x- бүрхүүлийн хэрэглээ:
![]() .
.
Жишээ 4Санамсаргүй хэмжигдэхүүний математик хүлээлтийг тодорхойл xГурван цохилттой цохилтын тоо, хэрэв сум тус бүрээр онох магадлал х = 0,4 .
Зөвлөмж: санамсаргүй хэмжигдэхүүний утгын магадлалыг олох Бернулли томъёо .
Хүлээгдэж буй шинж чанарууд
Математикийн хүлээлтийн шинж чанарыг авч үзье.
Үл хөдлөх хөрөнгө 1.Тогтмол утгын математикийн хүлээлт нь энэ тогтмолтой тэнцүү байна:
Үл хөдлөх хөрөнгө 2.Тогтмол хүчин зүйлийг хүлээлтийн тэмдгээс хасаж болно:
Эд хөрөнгө 3.Санамсаргүй хэмжигдэхүүний нийлбэрийн (ялгаа) математикийн хүлээлт нь тэдгээрийн математик хүлээлтийн нийлбэртэй (ялгаатай) тэнцүү байна.
Үл хөдлөх хөрөнгө 4.Санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдний математик хүлээлтийн үржвэртэй тэнцүү байна.
Эд хөрөнгө 5.Хэрэв санамсаргүй хэмжигдэхүүний бүх утгууд Xижил тоогоор буурах (өсөх). ХАМТ, дараа нь түүний математик хүлээлт ижил тоогоор буурах (өсөх) болно:
![]()
Зөвхөн математикийн хүлээлтээр хязгаарлагдах боломжгүй үед
Ихэнх тохиолдолд зөвхөн математикийн хүлээлт нь санамсаргүй хэмжигдэхүүнийг зохих ёсоор тодорхойлж чадахгүй.
Санамсаргүй хэмжигдэхүүнийг үзье XТэгээд ЮДараахь хуваарилалтын хуулиар өгөгдсөн:
| Утга X | Магадлал |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Утга Ю | Магадлал |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Эдгээр хэмжигдэхүүний математикийн хүлээлт ижил байна - тэгтэй тэнцүү:


Гэсэн хэдий ч тэдний тархалт өөр байна. Санамсаргүй утга Xзөвхөн математикийн хүлээлтээс ялгаатай утгууд болон санамсаргүй хэмжигдэхүүнийг авч болно Юматематикийн хүлээлтээс ихээхэн зөрүүтэй утгыг авч болно. Үүнтэй төстэй жишээ: дундаж цалин нь өндөр, бага цалинтай ажилчдын эзлэх хувийг дүгнэх боломжгүй юм. Өөрөөр хэлбэл, математикийн хүлээлтээр дор хаяж дунджаар ямар хазайлт гарах боломжтойг дүгнэж болохгүй. Үүнийг хийхийн тулд санамсаргүй хэмжигдэхүүний дисперсийг олох хэрэгтэй.
Дискрет санамсаргүй хэмжигдэхүүний тархалт
тархалтдискрет санамсаргүй хэмжигдэхүүн XМатематикийн хүлээлтээс хазайх квадратын математик хүлээлт гэж нэрлэдэг.

Санамсаргүй хэмжигдэхүүний стандарт хазайлт Xнь түүний дисперсийн квадрат язгуурын арифметик утга юм:
![]() .
.
Жишээ 5Санамсаргүй хэмжигдэхүүний дисперс ба стандарт хазайлтыг тооцоолох XТэгээд Ю, тэдгээрийн тархалтын хуулиудыг дээрх хүснэгтэд өгсөн болно.
Шийдэл. Санамсаргүй хэмжигдэхүүний математик хүлээлт XТэгээд Ю, дээр дурдсанчлан, тэгтэй тэнцүү байна. дисперсийн томъёоны дагуу Э(X)=Э(y)=0 бид дараахыг авна:


Дараа нь санамсаргүй хэмжигдэхүүний стандарт хазайлт XТэгээд Юбүрдүүлнэ
![]() .
.
Тиймээс ижил математикийн хүлээлттэй, санамсаргүй хэмжигдэхүүний дисперс Xмаш жижиг бөгөөд санамсаргүй Ю- чухал ач холбогдолтой. Энэ нь тэдний хуваарилалтын ялгааны үр дагавар юм.
Жишээ 6Хөрөнгө оруулагч нь өөр хөрөнгө оруулалтын 4 төсөлтэй. Хүснэгтэд эдгээр төслүүдийн хүлээгдэж буй ашгийн талаархи мэдээллийг холбогдох магадлалаар нэгтгэн харуулав.
| Төсөл 1 | Төсөл 2 | Төсөл 3 | Төсөл 4 |
| 500, П=1 | 1000, П=0,5 | 500, П=0,5 | 500, П=0,5 |
| 0, П=0,5 | 1000, П=0,25 | 10500, П=0,25 | |
| 0, П=0,25 | 9500, П=0,25 |
Альтернатив тус бүрийн хувьд математикийн хүлээлт, дисперс болон стандарт хазайлтыг ол.
Шийдэл. Гурав дахь хувилбарт эдгээр хэмжигдэхүүнийг хэрхэн тооцдог болохыг харуулъя.
Хүснэгтэд бүх хувилбаруудын олсон утгыг нэгтгэн харуулав.
Бүх хувилбарууд нь ижил математикийн хүлээлттэй байдаг. Энэ нь урт хугацаанд бүгд ижил орлоготой байна гэсэн үг. Стандарт хазайлтыг эрсдэлийн хэмжүүр гэж тайлбарлаж болно - энэ нь том байх тусам хөрөнгө оруулалтын эрсдэл их байх болно. Нэг их эрсдэл хүсэхгүй байгаа хөрөнгө оруулагч 1-р төслийг сонгох бөгөөд энэ нь хамгийн бага стандарт хазайлттай (0). Хэрэв хөрөнгө оруулагч богино хугацаанд эрсдэл, өндөр өгөөжийг илүүд үздэг бол тэрээр хамгийн том стандарт хазайлттай төслийг сонгох болно - төсөл 4.
Тархалтын шинж чанарууд
Дисперсийн шинж чанарыг танилцуулъя.
Үл хөдлөх хөрөнгө 1.Тогтмол утгын тархалт тэг байна:
Үл хөдлөх хөрөнгө 2.Тогтмол хүчин зүйлийг квадрат болгож дисперсийн тэмдгээс гаргаж болно.
![]() .
.
Эд хөрөнгө 3.Санамсаргүй хэмжигдэхүүний дисперс нь энэ утгын квадратын математик хүлээлттэй тэнцүү бөгөөд үүнээс тухайн утгын математик хүлээлтийн квадратыг хасна.
![]() ,
,
Хаана ![]() .
.
Үл хөдлөх хөрөнгө 4.Санамсаргүй хэмжигдэхүүний нийлбэр (ялгаа) нь тэдгээрийн дисперсийн нийлбэртэй (ялгаатай) тэнцүү байна:
Жишээ 7Дискрет санамсаргүй хэмжигдэхүүн гэдгийг мэддэг Xзөвхөн хоёр утгыг авна: −3 ба 7. Үүнээс гадна математикийн хүлээлт мэдэгдэж байна: Э(X) = 4. Дискрет санамсаргүй хэмжигдэхүүний дисперсийг ол.
Шийдэл. -ээр тэмдэглээрэй хсанамсаргүй хэмжигдэхүүн нь утгыг авах магадлал x1 = −3 . Дараа нь үнэ цэнийн магадлал x2 = 7 1 - байх болно х. Математикийн хүлээлтийн тэгшитгэлийг гаргая:
Э(X) = x 1 х + x 2 (1 − х) = −3х + 7(1 − х) = 4 ,
Бид магадлалыг хаанаас авах вэ: х= 0.3 ба 1 − х = 0,7 .
Санамсаргүй хэмжигдэхүүний тархалтын хууль:
| X | −3 | 7 |
| х | 0,3 | 0,7 |
Бид энэхүү санамсаргүй хэмжигдэхүүний дисперсийг дисперсийн 3-р шинж чанарын томъёог ашиглан тооцоолно.
Д(X) = 2,7 + 34,3 − 16 = 21 .
Санамсаргүй хэмжигдэхүүний математик хүлээлтийг өөрөө олж, дараа нь шийдлийг хар
Жишээ 8Дискрет санамсаргүй хэмжигдэхүүн Xзөвхөн хоёр утгыг авдаг. Энэ нь 0.4 магадлалтай 3 гэсэн том утгыг авна. Үүнээс гадна санамсаргүй хэмжигдэхүүний дисперсийг мэддэг Д(X) = 6. Санамсаргүй хэмжигдэхүүний математик хүлээлтийг ол.
Жишээ 9Нэг саванд 6 цагаан, 4 хар бөмбөлөг байдаг. 3 бөмбөгийг савнаас авдаг. Сугалсан бөмбөгнүүдийн дундах цагаан бөмбөгний тоо нь салангид санамсаргүй хэмжигдэхүүн юм X. Энэ санамсаргүй хэмжигдэхүүний математикийн хүлээлт ба дисперсийг ол.
Шийдэл. Санамсаргүй утга X 0, 1, 2, 3 утгуудыг авч болно. Харгалзах магадлалыг дараахаас тооцоолж болно. магадлалыг үржүүлэх дүрэм. Санамсаргүй хэмжигдэхүүний тархалтын хууль:
| X | 0 | 1 | 2 | 3 |
| х | 1/30 | 3/10 | 1/2 | 1/6 |
Иймээс энэ санамсаргүй хэмжигдэхүүний математик хүлээлт:
М(X) = 3/10 + 1 + 1/2 = 1,8 .
Өгөгдсөн санамсаргүй хэмжигдэхүүний дисперс нь:
Д(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Тасралтгүй санамсаргүй хэмжигдэхүүний математикийн хүлээлт ба тархалт
Тасралтгүй санамсаргүй хэмжигдэхүүний хувьд математикийн хүлээлтийн механик тайлбар нь ижил утгыг хадгалах болно: нягтралтай x тэнхлэгт тасралтгүй тархсан нэгж массын массын төв. е(x). Дискрет санамсаргүй хэмжигдэхүүнээс ялгаатай нь функц нь аргумент болдог xбигэнэт өөрчлөгддөг, тасралтгүй санамсаргүй хувьсагчийн хувьд аргумент тасралтгүй өөрчлөгддөг. Гэхдээ тасралтгүй санамсаргүй хэмжигдэхүүний математикийн хүлээлт нь түүний дундаж утгатай бас холбоотой.
Тасралтгүй санамсаргүй хэмжигдэхүүний математик хүлээлт ба дисперсийг олохын тулд тодорхой интегралуудыг олох хэрэгтэй. . Хэрэв тасралтгүй санамсаргүй хэмжигдэхүүний нягтын функц өгөгдсөн бол энэ нь интегралд шууд орно. Хэрэв магадлалын тархалтын функц өгөгдсөн бол түүнийг ялгах замаар нягтын функцийг олох хэрэгтэй.
Тасралтгүй санамсаргүй хэмжигдэхүүний бүх боломжит утгуудын арифметик дундажийг түүний гэж нэрлэдэг математикийн хүлээлт, эсвэл гэж тэмдэглэнэ.
Шийдэл:
6.1.2 Хүлээгдэж буй шинж чанарууд
1. Тогтмол утгын математикийн хүлээлт нь тогтмолтой тэнцүү байна.
2. Хүлээлтийн тэмдгээс тогтмол хүчин зүйлийг гаргаж болно. ![]()
3. Хоёр бие даасан санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдгээрийн математик хүлээлтийн үржвэртэй тэнцүү байна.
Энэ шинж чанар нь дурын тооны санамсаргүй хэмжигдэхүүнд хүчинтэй.
4. Хоёр санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт нь гишүүдийн математик хүлээлтийн нийлбэртэй тэнцүү байна.
Энэ шинж чанар нь дурын тооны санамсаргүй хэмжигдэхүүнд мөн үнэн юм.
Жишээ: М(X) = 5, M(Y)= 2. Санамсаргүй хэмжигдэхүүний математик хүлээлтийг ол З, хэрэв энэ нь мэдэгдэж байгаа бол математикийн хүлээлтийн шинж чанарыг ашиглах Z=2X + 3Y.
Шийдэл: M(Z) = M(2X + 3Y) = M(2X) + M(3Y) = 2М(X) + 3М(Ү) = 2∙5+3∙2 =
1) нийлбэрийн математик хүлээлт нь математикийн хүлээлтийн нийлбэртэй тэнцүү байна
2) хүлээлтийн тэмдгээс тогтмол хүчин зүйлийг авч болно
p-тэй тэнцүү А үйл явдал тохиолдох магадлалыг n бие даасан туршилт хийцгээе. Тэгвэл дараах теоремыг баримтална.
Теорем. n бие даасан туршилтын үед А үйл явдал тохиолдсон тоон математикийн хүлээлт M(X) нь туршилтын тоо болон туршилт тус бүрт тохиолдох магадлалын үржвэртэй тэнцүү байна.
6.1.3 Дискрет санамсаргүй хэмжигдэхүүний дисперс
Математикийн хүлээлт нь санамсаргүй үйл явцыг бүрэн тодорхойлж чадахгүй. Математикийн хүлээлтээс гадна санамсаргүй хэмжигдэхүүний утгуудын математик хүлээлтээс хазайлтыг тодорхойлдог утгыг нэвтрүүлэх шаардлагатай.
Энэ хазайлт нь санамсаргүй хэмжигдэхүүн ба түүний математик хүлээлтийн зөрүүтэй тэнцүү байна. Энэ тохиолдолд хазайлтын математикийн хүлээлт тэг байна. Үүнийг зарим боломжит хазайлт нь эерэг, бусад нь сөрөг, харилцан цуцалсны үр дүнд тэгийг авсантай холбон тайлбарлаж байна.
Тархалт (тархалт)Дискрет санамсаргүй хэмжигдэхүүнийг түүний математик хүлээлтээс санамсаргүй хэмжигдэхүүний квадрат хазайлтын математик хүлээлт гэнэ.
Практикт дисперсийг тооцоолох энэ арга нь тохиромжгүй, учир нь санамсаргүй хэмжигдэхүүний олон тооны утгуудын хувьд төвөгтэй тооцоолол хийхэд хүргэдэг.
Тиймээс өөр аргыг ашигладаг.
Теорем. Дисперс нь X санамсаргүй хэмжигдэхүүний квадратын математик хүлээлт ба түүний математик хүлээлтийн квадратын зөрүүтэй тэнцүү байна..
Баталгаа. Математикийн хүлээлт M (X) ба математикийн хүлээлт M 2 (X) квадрат нь тогтмол утгатай болохыг харгалзан бид дараахь зүйлийг бичиж болно.
Жишээ. Тархалтын хуулиар өгөгдсөн дискрет санамсаргүй хэмжигдэхүүний дисперсийг ол.
| X | ||||
| X 2 | ||||
| Р | 0.2 | 0.3 | 0.1 | 0.4 |
Шийдэл: .
6.1.4 Тархалтын шинж чанар
1. Тогтмол утгын дисперс нь тэг байна. .
2. Тогтмол коэффициентийг квадратаар тараах тэмдгээс гаргаж болно. ![]() .
.
3. Хоёр бие даасан санамсаргүй хэмжигдэхүүний нийлбэрийн дисперс нь эдгээр хувьсагчийн дисперсийн нийлбэртэй тэнцүү байна. .
4. Хоёр бие даасан санамсаргүй хэмжигдэхүүний ялгаврын дисперс нь эдгээр хувьсагчийн дисперсийн нийлбэртэй тэнцүү байна. .
Теорем. Үйл явдал тохиолдох магадлал p нь тогтмол байх n бие даасан туршилтын А үйл явдлын тооны хэлбэлзэл нь туршилтын тоо болон туршилт бүрийн тохиолдлын магадлалын үржвэртэй тэнцүү байна.
Жишээ нь: DSV X-ийн дисперсийг ол - 2 бие даасан туршилтын А үйл явдлын тохиолдлын тоог, хэрэв эдгээр туршилтуудад тохиолдох магадлал ижил бөгөөд M(X) = 1.2 гэдгийг мэддэг бол.
Бид 6.1.2-ын теоремыг хэрэглэнэ.
M(X) = np
М(X) = 1,2; n= 2. Олно х:
1,2 = 2∙х
х = 1,2/2
q = 1 – х = 1 – 0,6 = 0,4
Тархалтыг дараах томъёогоор олъё.
D(X) = 2∙0,6∙0,4 = 0,48
6.1.5 Дискрет санамсаргүй хэмжигдэхүүний стандарт хазайлт
Стандарт хэлбэлзэлХ санамсаргүй хэмжигдэхүүнийг дисперсийн квадрат язгуур гэнэ.
![]() (25)
(25)
Теорем. Хязгаарлагдмал тооны харилцан хамааралгүй санамсаргүй хэмжигдэхүүний нийлбэрийн стандарт хазайлт нь эдгээр хувьсагчийн квадрат стандарт хазайлтын нийлбэрийн квадрат язгууртай тэнцүү байна.
6.1.6 Дискрет санамсаргүй хэмжигдэхүүний горим ба медиан
Fashion M эсвэл DSVсанамсаргүй хэмжигдэхүүний хамгийн их магадлалтай утгыг (өөрөөр хэлбэл хамгийн өндөр магадлалтай утгыг) гэж нэрлэдэг.
Медиан M e DSVтархалтын цувааг хагасаар хуваах санамсаргүй хэмжигдэхүүний утга юм. Хэрэв санамсаргүй хэмжигдэхүүний утгуудын тоо тэгш байвал медианыг хоёр дундаж утгын арифметик дундаж гэж үзнэ.
Жишээ: DSW-ийн горим ба медианыг ол X:
| X | ||||
| х | 0.2 | 0.3 | 0.1 | 0.4 |
Би = = 5,5
Ахиц дэвшил
1. Энэхүү ажлын онолын хэсэгтэй (лекц, сурах бичиг) танилцах.
2. Өөрийн сонголтын дагуу даалгавраа гүйцэтгээрэй.
3. Ажлын тайланг эмхэтгэх.
4. Ажлаа хамгаал.
2. Ажлын зорилго.
3. Ажлын явц.
4. Өөрийн сонголтын шийдвэр.
6.4 Бие даасан ажилд зориулсан даалгаврын хувилбарууд
Сонголт дугаар 1
1. Тархалтын хуулиар өгөгдсөн DSV X-ийн математик хүлээлт, дисперс, стандарт хазайлт, горим, медианыг ол.
| X | ||||
| П | 0.1 | 0.6 | 0.2 | 0.1 |
2. X ба Y-ийн математик хүлээлт мэдэгдэж байгаа бол санамсаргүй хэмжигдэхүүн Z-ийн математик хүлээлтийг ол: M(X)=6, M(Y)=4, Z=5X+3Y.
3. DSV X-ийн дисперсийг ол - хоёр бие даасан туршилтын үед А үйл явдлын тохиолдлын тоог, хэрэв эдгээр туршилтуудын үйл явдлын магадлал ижил бөгөөд M (X) = 1 гэдгийг мэддэг бол.
4. Дискрет санамсаргүй хэмжигдэхүүний боломжит утгуудын жагсаалтыг өгсөн болно X: x 1 = 1, x2 = 2, x 3= 5, мөн энэ хэмжигдэхүүн болон түүний квадратын математик хүлээлт нь мөн мэдэгдэж байна: , . Боломжит утгуудад харгалзах , , , магадлалыг олж, DSW-ийн тархалтын хуулийг гарга.
Сонголт дугаар 2
| X | ||||
| П | 0.3 | 0.1 | 0.2 | 0.4 |
2. X ба Y-ийн математик хүлээлт мэдэгдэж байгаа бол санамсаргүй хэмжигдэхүүн Z-ийн математик хүлээлтийг ол: M(X)=5, M(Y)=8, Z=6X+2Y.
3. DSV X-ийн дисперсийг ол - 3 бие даасан туршилтын А үйл явдлын тохиолдлын тоог, хэрэв эдгээр туршилтуудын тохиолдлын магадлал ижил бөгөөд M (X) = 0.9 гэдгийг мэддэг бол.
4. Х дискрет санамсаргүй хэмжигдэхүүний боломжит утгуудын жагсаалтыг өгсөн болно. x 1 = 1, x2 = 2, x 3 = 4, x4= 10, мөн энэ хэмжигдэхүүн болон түүний квадратын математик хүлээлт нь мэдэгдэж байна: , . Боломжит утгуудад харгалзах , , , магадлалыг олж, DSW-ийн тархалтын хуулийг гарга.
Сонголт дугаар 3
1. Тархалтын хуулиар өгөгдсөн DSV X-ийн математик хүлээлт, дисперс ба стандарт хазайлтыг ол.
| X | ||||
| П | 0.5 | 0.1 | 0.2 | 0.3 |
2. X ба Y-ийн математик хүлээлт нь мэдэгдэж байвал санамсаргүй хэмжигдэхүүн Z-ийн математик хүлээлтийг ол: M(X)=3, M(Y)=4, Z=4X+2Y.
3. DSV X-ийн дисперсийг ол - дөрвөн бие даасан туршилт дахь А үйл явдлын тохиолдлын тоог, хэрэв эдгээр туршилтуудын үйл явдлын магадлал ижил бөгөөд M (x) = 1.2 гэдгийг мэддэг бол.
Өмнө нь мэдэгдэж байгаагаар тархалтын хууль нь санамсаргүй хэмжигдэхүүнийг бүрэн тодорхойлдог. Гэсэн хэдий ч түгээлтийн хууль нь ихэвчлэн тодорхойгүй байдаг тул хүн өөрийгөө бага мэдээллээр хязгаарлах ёстой. Заримдаа санамсаргүй хэмжигдэхүүнийг нийтлэх тоог ашиглах нь бүр илүү ашигтай байдаг; ийм тоонуудыг дууддаг санамсаргүй хэмжигдэхүүний тоон шинж чанар.
Математикийн хүлээлт нь чухал тоон шинж чанаруудын нэг юм.
Математикийн хүлээлт нь санамсаргүй хэмжигдэхүүний дундаж утгатай ойролцоогоор тэнцүү байна.
Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлтЭнэ нь түүний бүх боломжит утгууд ба тэдгээрийн магадлалын бүтээгдэхүүний нийлбэр юм.
Хэрэв санамсаргүй хэмжигдэхүүн нь хязгаарлагдмал тархалтын цуваагаар тодорхойлогддог бол:
| X | x 1 | x 2 | x 3 | … | x n |
| Р | х 1 | х 2 | х 3 | … | r p |
дараа нь математикийн хүлээлт М(X)томъёогоор тодорхойлно:
Тасралтгүй санамсаргүй хэмжигдэхүүний математик хүлээлтийг тэгшитгэлээр тодорхойлно.
санамсаргүй хэмжигдэхүүний магадлалын нягтрал хаана байна X.
Жишээ 4.7.Шоо шидэхэд хэдэн оноо унах вэ гэсэн математик хүлээлтийг ол.
Шийдэл:
Санамсаргүй утга X 1, 2, 3, 4, 5, 6 утгуудыг авна. Түүний тархалтын хуулийг хийцгээе:
| X | ||||||
| Р |
Дараа нь математикийн хүлээлт нь:
Математикийн хүлээлтийн шинж чанарууд:
1. Тогтмол утгын математикийн хүлээлт нь тогтмолтой тэнцүү байна:
M(S)=S.
2. Тогтмол хүчин зүйлийг хүлээлтийн тэмдгээс хасаж болно:
M(CX) = CM(X).
3. Хоёр бие даасан санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдгээрийн математик хүлээлтийн үржвэртэй тэнцүү байна.
M(XY) = M(X)M(Y).
Жишээ 4.8. Бие даасан санамсаргүй хэмжигдэхүүнүүд XТэгээд ЮДараахь хуваарилалтын хуулиар өгөгдсөн:
| X | Ю | ||||||
| Р | 0,6 | 0,1 | 0,3 | Р | 0,8 | 0,2 |
XY санамсаргүй хэмжигдэхүүний математик хүлээлтийг ол.
Шийдэл.
Эдгээр хэмжигдэхүүн бүрийн математик хүлээлтийг олцгооё.
санамсаргүй хэмжигдэхүүн XТэгээд Юбие даасан, тиймээс хүссэн математикийн хүлээлт:
M(XY) = M(X)M(Y)=
Үр дагавар.Хэд хэдэн харилцан бие даасан санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь тэдний математик хүлээлтийн үржвэртэй тэнцүү байна.
4. Хоёр санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэр томъёоны математик хүлээлтийн нийлбэртэй тэнцүү байна.
M(X + Y) = M(X) + M(Y).
Үр дагавар.Хэд хэдэн санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэр томъёоны математик хүлээлтийн нийлбэртэй тэнцүү байна.
Жишээ 4.9. 3 удаагийн буудлага нь бай онох магадлалтай тэнцүү байна х 1 = 0,4; p2= 0.3 ба х 3= 0.6. Нийт цохилтын тооны математик хүлээлтийг ол.
Шийдэл.
Эхний цохилтын цохилтын тоо нь санамсаргүй хэмжигдэхүүн юм X 1, энэ нь зөвхөн хоёр утгыг авч болно: 1 (цохих) магадлал бүхий х 1= 0.4 ба 0 (алдсан) магадлал бүхий q 1 = 1 – 0,4 = 0,6.
Эхний цохилт дахь цохилтын тооны математикийн хүлээлт нь цохих магадлалтай тэнцүү байна.
Үүнтэй адилаар, бид хоёр, гурав дахь цохилтын тоонуудын математикийн хүлээлтийг олдог.
М(X 2)= 0.3 ба M (X 3) \u003d 0,6.
Нийт цохилтын тоо нь мөн гурван цохилт тус бүрийн цохилтын нийлбэрээс бүрдэх санамсаргүй хэмжигдэхүүн юм.
X \u003d X 1 + X 2 + X 3.
Хүссэн математикийн хүлээлт XБид математикийн теоремоор нийлбэрийн хүлээлтийг олдог.